正答率と運動の習慣の関連性に関する調査の結果

こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます！
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
なかなか増えないアクセス数に一喜一憂するのが日課。

前回は、間取り図から部屋割りを推測する問題をやりましたね。
国家総合職でほぼ毎年出題されている対応関係の問題なので、解いてない方はぜひ挑戦してみてください。
もう解いた方も、ある程度時間が経ったら解き直してみてください。
これは、解法を頭に入れることはもちろんですが、自分の手で解くことによって、新たな発見があるからです。
この段階では、正答にたどり着けなくても大丈夫です。
解き直して途中で手詰まったら、その「手詰まった感覚」を持ちながらもう一度解説を読み込んでみてください。
手詰まった原因を解消する、という目的を持ちながら解説に向かうことで、1回目とは異なった視点から解法を検討できるようになります。
これを繰り返すことで、解法をただの知識でなく、活用できる知恵としてストックされていき、やがては自力で正答を導き出すことができます。
そうした「知恵」の積み重ねこそ、すなわち初見の問題への対応力なのです。
新しい問題を解いたら、ぜひ忘れずに解き直しすることをおすすめします。

復習がバッチリな方は、本日の問題へ参りましょう！

本日の演習問題

性別、週あたりの運動の時間、試験の正答率という3つのカテゴリに属する人数に関する問題です。
まずは現時点で分かっていることを整理しましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。

それではスタート！

詳しい解説

3つの集合（性別、運動時間、正答率）が与えられて、それらに属する人数が問題になっているような場合は、キャロル表を作成して人数の内訳を明らかにしましょう。

今回は、性別、運動時間、正答率という3つのカテゴリを次図のように配置し、進めます。

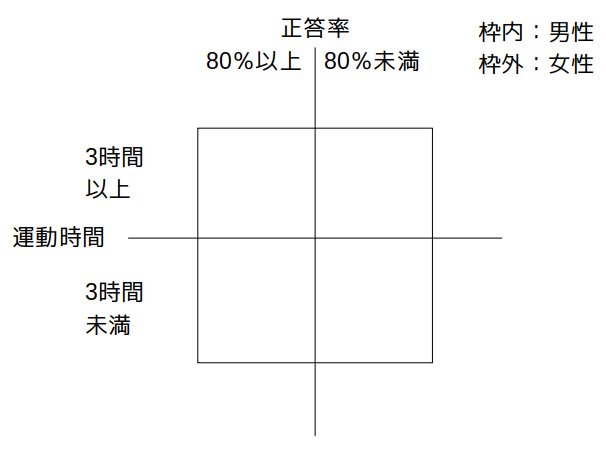
まずは分かっていることを記入します。
「男性は600人」、「運動する時間が週に3時間未満の者は500人、週に3時間以上の者は500人」、「試験の正答率が80％以上の者は300人、80％未満の者は700人」、「運動する時間が週に3時間未満の男性は250人」、「試験の正答率が80％以上の女性は150人」を記入すると、次のようになります。

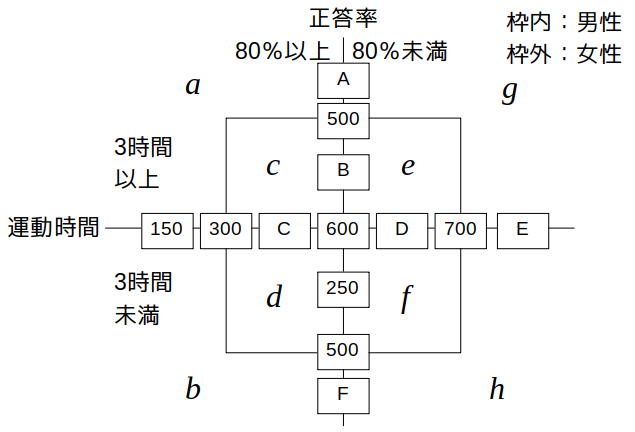
現時点で分かってない数字をアルファベット（A〜F、a〜h）でおきました。

次に、記入した数字から分かる部分を埋めていきます。
まずBについて、B+250=600より、B＝350（人）
これより、Aについて、A+B=500より、A＝150（人）

またCについて、C+150=300より、C＝150（人）
これより、Dについて、C+D＝600より、D＝450（人）
さらにEについて、D+E＝700より、E=250（人）

最後にFについて、F+250＝500より、F＝250（人）

以上を記入した図は次のようになります。

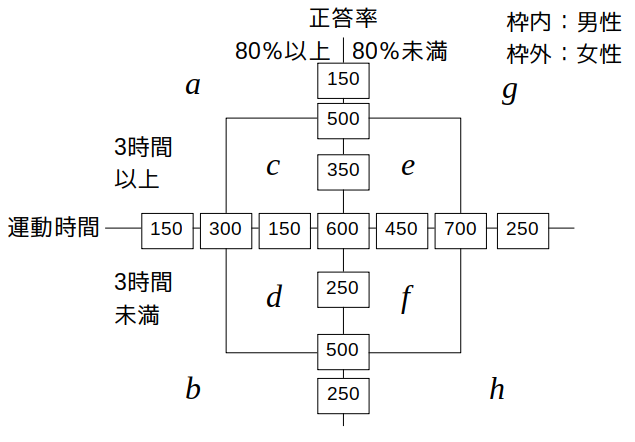
条件から分かるのはここまでなので、あとはこの図をもとに選択肢を検討しましょう。

１の正誤

キャロル表によると、「運動する時間が週に3時間以上の男性の人数」は350人、「試験の正答率が80％以上の男性の人数」は150人なので、2倍を超えており誤りです。

２の正誤

キャロル表によると、「運動する時間が週に3時間以上の女性」の人数は150人です。
一方、「運動する時間が週に3時間以上で試験の正答率が80％未満の男性」の人数（=\(e\)）は、\(c+e=350\)より\(e=350-c\)ですが、\(c\)の値は確定しないので\(e\)も決まらず、\(e\)は350人以下であるところまでしか分かりません。
よって２は必ずしも正しいとはいえないので誤りです。

３の正誤

キャロル表によると、「運動する時間が週に3時間以上で試験の正答率が80％以上の男性」の人数（=\(c\)）は、\(c+d=150\)より\(c=150-d\)ですが、前項と同様に、\(c\)は150人以下である、ということまでしか分かりません。
さらに、「運動する時間が週に3時間未満で試験の正答率が80％未満の男性」の人数（=\(f\)）についても、\(f=250-d\)より、250人以下であることしか分かりません。
よって３は必ずしも正しいとはいえないので誤りです。

４の正誤

キャロル表によると、「試験の正答率が80％以上の女性」の人数は150人です。
一方、「運動する時間が週に3時間未満で試験の正答率が80％未満の男性」の人数（=\(f\)）は、前項の通り250人以下であることまでしか分かりません。
よって４は必ずしも正しいとはいえないので誤りです。

５の正誤

キャロル表によると、「運動する時間が週に3時間未満で試験の正答率が80％以上の女性」の人数（=\(b\)）は、\(a+b=150\)より\(b=150-a\)
一方、「運動する時間が週に3時間以上で試験の正答率が80％未満の女性」の人数（=\(g\)）は、\(a+g=150\)より\(g=150-a\)なので、\(b=g\)であることが分かる。
よって５は確実に正しいといえます。

よって、５が正解です。

おわりに

お疲れ様でした！
いかがだったでしょうか？

3つの集合に属する人数を明らかにする問題でした。
3集合の要素数の内訳を知りたいときは、キャロル表を用いるのが有効です。
各集合を図に配置したら、まずは与えられた通りに要素数を書き込んでいきます。
書き込んだら、あとは計算で分かる部分を埋めていけばOKです。
国家総合職では特にですが、この手の問題で全ての数値が明らかになることはまずないと考えて良いでしょう。
分かる範囲で数値を書き込んだら、あとは本問のように選択肢を個別に検証していくしかありません。
この辺りは判断推理の対応関係などにも共通する、ある種「お決まりのパターン」です。

キャロル表は、ベン図とともに集合分野の問題によく用いられる道具の一つですが、ベン図に比べると馴染みの薄い方が多いのではないでしょうか。（ちなみに私は公務員試験で初めてその存在を知りました。だって学校で教わらなかったし……）
今回はキャロル表そのものの説明は省いてますが、使い方が分からない方は参考書を使ってよく練習しておいてください。
国家総合職の数的処理では、集合の問題は頻出というほどのものではありませんが、数年ごとに出題されているので、ある程度の対策は必要でしょう。
頻出ではないからといって全くのノータッチですと、易しめの問題が出たときに、周りは得点しているのに自分だけ解けないとなると最悪です。
本問が難しいと感じられたら、この機会にキャロル表を徹底的に対策してみてはいかがでしょう？
以前にも似た問題を解説しているので、まだ見てなければぜひチェックしてみてください↓

アンケート結果に基づく人数の集計

本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします！

次回もお楽しみに！

略解