こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
一万円あったら、ゆでたまごがキレイに向ける能力が欲しい。
前回は、くじ引きの景品の位置関係を明らかにする問題をやりましたね。
国家総合職の判断推理には欠かすことのできない位置関係の問題なので、解いてない方はぜひ挑戦してみてください。
今回のテーマは「展開図」です。
展開図の攻略に欠かせないテクニック、「面移動」の習得は完ぺきですか?
不安のある方は、以下の記事で面移動の考え方をていねいに解説してるので、オススメです!
演習問題:展開図の組み立て
図のような展開図を持つ立体において、面Pと向かい合う面は次のうちどれか。
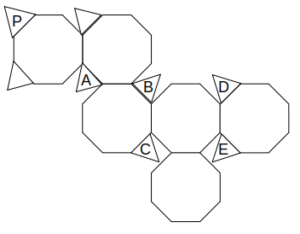
- A
- B
- C
- D
- E
2
空間図形の展開図がテーマの問題です。
脳内で立体を組み上げられればそれで解決しますが、このままではなかなか難しいでしょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
展開図は、切れ目を入れる辺によって形が変わります。
言い換えれば、元々一つだった辺なら自在にくっつけたり切り離したりして、展開図の形を変えてもいいんです。
これを利用して、もとの立体の形状をイメージしやすいように展開図を書き換えちゃいましょう!
……というのが「面移動」のテクニックです。

立体をイメージするより、展開図のどの辺とどの辺がくっついていたかを考える方がラク
隣り合う辺は回転による面移動も有効
滑らない回転移動
まず三角形について、散らばっていると組み立てづらいので、一つの八角形に集めてしまいましょう。
隣接する辺は一致するので、次のように三角形を移動できます。
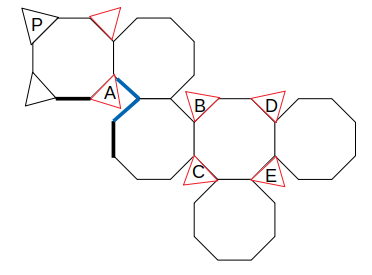
さらに、展開図の左半分を組み上げた様子を想像してみると、図に黒い太線で示した2辺が重なることが分かります。
よって、展開図で一番左の八角形(+三角形4つ)を次のように移動することができます。

上図の青い太線に沿って滑ることなく回転させたのと同じ
部分的に組み立ててみるのも時には有効
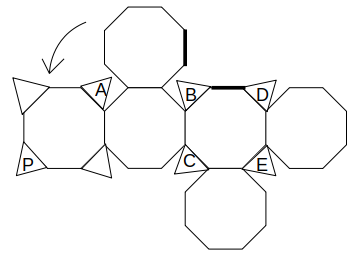
同様に、元の立体において上図の太線が一致することから、次のように八角形を移動します。
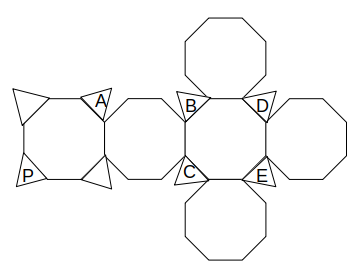
空間図形をある程度勉強した方なら、この展開図の形に見覚えがあるはず。

立方体のヤツ
お気づきの通り、本問の立体は立方体を基礎に作られています。
三角形を全て「点」に置き換えてしまえば、立方体の展開図そのものになります。
ここまで来れば、頭の中で立体を組み上げることはそう難しくないですね。
書き換えた展開図を立方体のそれとして考えると、Pの対面に来るのはBになります。

PとBを結ぶと対角線になるよ
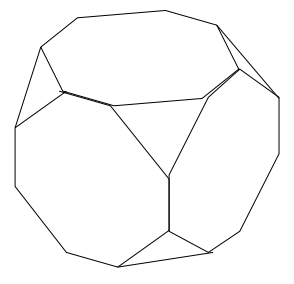
よって、2が正解です。
おわりに:展開図のコツは面移動
お疲れ様でした!
いかがだったでしょうか?
展開図には面移動が有効です。
隣り合う辺同士であれば、回転による移動も可能です。
展開図で、完成図をイメージしやすい形に変形するのは定石です。
元々は一つだった辺同士なら、くっつけたり切り離したりすることができます。
そのような辺を見つけるためには、頭の中で組み立ててみる必要がありますが、苦手な方は解説にあるような「滑らない回転」をイメージしましょう。
これは「隣り合う辺は元々くっついて一つだった」という考えに基づいたものになります。
隣り合う辺がくっついて隣になったらそれらもまたくっつけることができて……という具合です。
余談ですが、本問で作った立体は切頂六面体といって、立方体の角を切り取ったものになってます。
最初に与えられた展開図からこのことに気づくのはなかなか難しいですが、八角形のつながりが立方体の展開図の1パターンに似ているところから類推することもできます。
そこに気づけなかったとしても、面移動を知っていれば解けます。

切頂八面体の展開図を扱った問題もあるよ
国家総合職では、空間図形の問題が例年1〜2問出題されています。
苦手な方も、捨ててしまいたくなる気持ちは分かりますが、定石だけでもマスターしましょう。
本サイトで扱っている問題はどれも過去問に近いレベルのものなので、解けなくてもそんなに落ち込まないで大丈夫です。
他でカバーすることもできますし。
よっぽど難しい場合は、基礎(=参考書)に立ち返ってみるのも一考です。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
展開図において隣り合う2辺は、切り開く前の立体では同一の辺であったことから、次図のように三角形を移動させることができる。
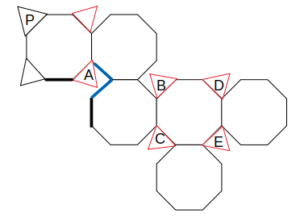
三角形の移動
さらに、この図の青線に沿って八角形(+三角形)を回転移動させることができ、黒い太線を一致させた次の展開図を得る。
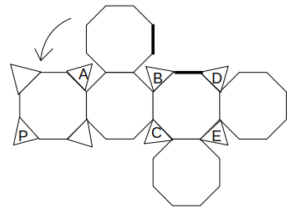
八角形の回転移動1
また、組み立てた立体において、この図に示す太線は一致していたと考えられるから、次のように八角形を移動させることができる。
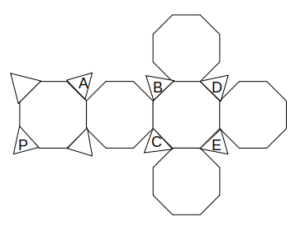
八角形の回転移動2
これより、組み立てた立体は立方体の角を切り取ったものとなると分かる。(切頂六面体)
面Pと向かい合うのはBである。
よって、正解は2である。

コメント