こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
サイトを立ち上げる前から作っておいた問題のストックがとうとう底をつきました。
これからは問題を作るのと記事を書くのと同時並行になるけど、毎日更新のペースは落とさず頑張りたい。
前回は、箱の中身を入れ替える操作手順の問題をやりましたね。
解き方の要点は思い出せますか?
忘れてしまった方は、簡単にでもいいので再度見返すことをおすすめします。
「そういえばこんな解き方だったな〜」と振り返るのが大事です。
空中で思い出すだけなら、ちょっとしたスキマ時間にもできるので、日々の習慣に取り入れると勉強の効果がアップしますよ!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
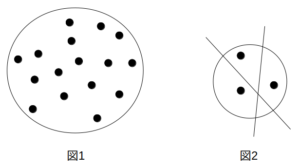
内部に16個の点が描かれた円形の領域を、何本かの直線により分割することを考える(図1)。16個の点が1個ずつ別の領域に分かれるように切り分けるためには、最低何本の直線を引く必要があるか。たとえば、円の中に3個の点が存在する場合は、図2のように最低2本の直線が必要となる。
- 4本
- 5本
- 6本
- 7本
- 8本
2
円形の領域を直線で分割する問題ですね。
直線が2本の場合が例示されてますが、3本の場合はどうなるでしょう。
以下で詳しく解説します。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただいても問題ありません。
それではスタート!
詳しい解説
円に対して直線を引くとき、内部はいくつの領域に分かれるでしょう?
点を別々の領域に分けるなら、少なくとも点の数(=16個)の分だけ領域を用意する必要があります。
かつ、「最低何本の直線が必要か?」と聞かれているので、より少ない本数で16個の領域を確保しなければなりません。
結局、「円に直線を1本引いたときに増える領域の数」を順に数えていくとき、合計16個以上の領域ができるのは何本目か?を考えることになります。
問題文に、例として直線が2本の場合が与えられています。
これも大事なヒントです。
ぜひ活用しましょう。
直線が2本のとき、円の内部は4つの領域に分けられています。
ここに直線を1本追加するとき、領域はいくつ増やせるでしょう?
すでにある直線と平行でなく、かつ1点で交わることのない(※)直線を追加してみましょう。
(※これは少ない本数で最大個数の領域を得るための前提条件です)
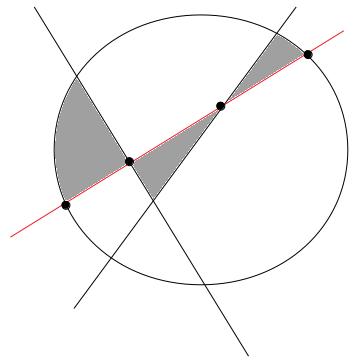
2本の直線で4分割された領域に直線(赤)を1本足すと、直線は円および他の直線と4点で交わり、灰色で示す3つの領域が新たに追加されます。
これにより、円の内部は4+3=7個の領域に分けられました。
もう1本追加してみましょう。
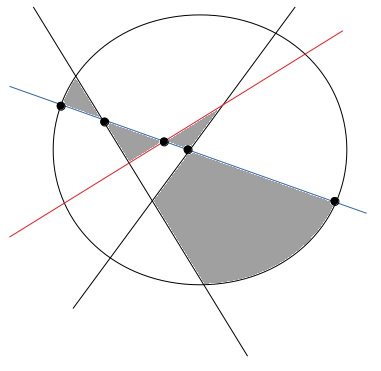
もう1本の直線(青)を加えると、直線は円および他の直線と5点で交わり、灰色で示す4つの領域が新たに追加されます。
これにより、円の内部は7+4=11個の領域に分けられました。
ここまでの結果から、円および他の直線と交わる点の数がnだとしたら、追加される領域はn-1かな、と予測できた方、素晴らしいです!
さらに元あった領域の数に、n-1を足せば新しい領域の数になる、というところまで気づけばあと一歩。
ここまで推測できれば、あとは実際に図を描かなくても領域の数を知ることができます。
5本目の直線\(l\)を加えたときの領域数を考えてみましょう。
まず、\(l\)は外側の円と2点で交わります。
加えてそこにはすでに4本の直線があり、(※)のように、最大数の領域を得るにはこれら4本全てと1回ずつ交わることになります。
すると、\(l\)上の交点は全部で2+4=6個なので、6-1=5個の領域が新たに追加されることになります。
直線が4本のとき領域は11個あったので、\(l\)によって11+5=16個の領域に分けられます。
16個の領域を確保できることさえ分かれば、あとは直線の引き方次第で16個の点を別の領域に入れることができます。
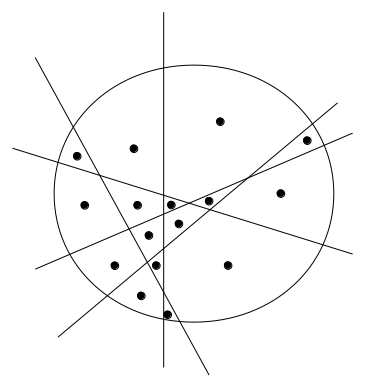
以上より、16個の点を別々の領域に分けるのに必要な直線の本数は5本なので、2が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
円形の領域を分割するのに必要な直線の本数を求める問題でした。
一般化できなかったとしても、5本くらいなら最悪図を描いても解くことができます。
その際は(※)の前提条件にだけ注意してください。
全ての直線に交わらないと、得られる領域の数は少なくなってしまいます。
(領域の数は交点の数で決まるのでしたね)
領域分割の問題は参考書では必ず扱うテーマであり、他にはこれといってひねった要素もなかったので、数的処理をある程度勉強した方なら解けてしまった方も多いのではないでしょうか。
国家総合職を目指す方であれば、本番なら必ず得点したい問題の一つだったと私は思います。
実は、本番でもこういうありがちな問題が出題されることはあるんです。
ですから、そういう場合にはぜひとも落とさずに得点にしてほしいと思います。
基本事項の大切さを改めて教えてくれる、そんな問題でした。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
円形の領域に対して直線を1本ずつ追加していき、分割された領域の数が初めて16以上となるときの直線の本数が分かればよい。
まず、直線が2本の場合、得られる領域の数は4つである。
ここに、すでにある直線と平行でなく、かつ1点で交わることのないような直線(赤)を1本追加する(計3本)と、直線は円および他の直線と4点で交わり、次図に灰色で示す3つの領域が新たに追加される。
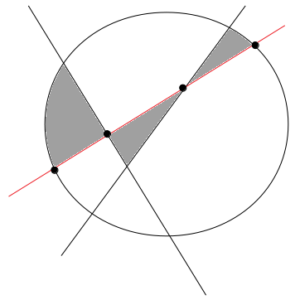
直線が3本のときの領域
次に、直線をさらに1本追加(計4本)することを考える。(青線)
直線は円および他の直線と5点で交わり、次図に灰色で示す4つの領域が新たに追加される。
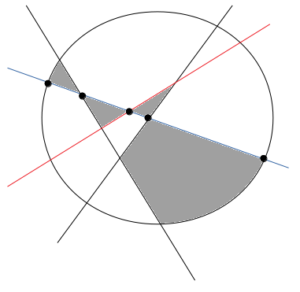
直線が4本のときの領域
これにより、円の内部には7+4=11個の領域ができる。
一般に、円形の領域がn本の直線によってk個の領域に分割されているとき、そこにn+1本目の直線を追加すると、n+1本目の直線はn+2個の交点を持つので、新たにn+1個の領域が追加される。
このことより、5本目の直線を追加したときの領域の数は11+5=16個であると分かる。
これが16個の領域を得るのに必要な直線の最小数であり、16個の点を別々の領域に分けるのに必要な本数である。
したがって、正解は2である。

コメント