こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「面積(平面図形)」
本サイトでは、面積の問題にはパターンがある、と説明しています。
次の2つ。
- 大きさが分かっている図形との相似比から求める方法
- 具体的に長さを求めて面積公式に当てはめる方法
面積の問題を見たら、
相似比か、公式か
を見極めましょう。
どちらのパターンかが分かると、解答の方針が立ちます。
相似比 → 比の関係が必要→相似な図形はないかな?
公式 → 辺や線分の長さが必要→長さを書き出してみよう
といったように。
今回は、平面図形の面積の問題を解説。
例によって、数的処理の過去問みたいなやつです。

高校受験相当の知識があればOK
演習問題:接する円のすき間の面積
図のように、互いに接する半径の等しい2つの円A,Bと半径2の半円に対し、共通接戦\(l\)を引く。このとき、灰色の部分の面積はいくらか。
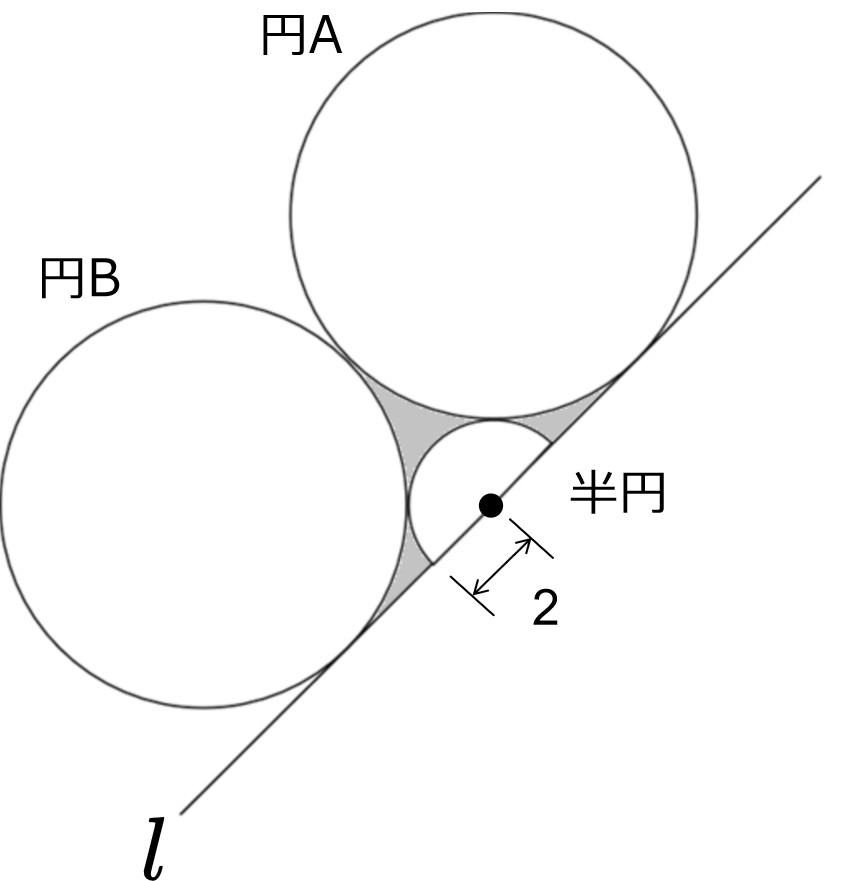
- \(8(2 + 2 \sqrt{2}) – 4(1 + \sqrt{2}) \pi\)
- \(8(3 + 2 \sqrt{2}) – 4(2 + \sqrt{2}) \pi\)
- \(8(3 + 2 \sqrt{2}) – 4(3 + \sqrt{2}) \pi\)
- \(8(3 + 2 \sqrt{2}) – 4(2 + 3\sqrt{2}) \pi\)
- \(8(3 + \sqrt{2}) – 4(2 + \sqrt{2}) \pi\)
2
「接する」がキーワード。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:円の面積の公式には半径が必要
面積の問題は、まず
相似比か公式か
を考えること。
本問は公式を使うパターンになってます。

半径が与えられてるし円には公式がある
とはいえ、直接求めるのは不可能。
公式が使える図形を探し、間接的に求めるしかありません。
平面図形といえば……補助線
平面図形には補助線:中心と接点を結ぶ
補助線を使って、公式が使える図形を見つけられますか?
本問で特徴的な点は、「中心」と「接点」
結んでみると、、、
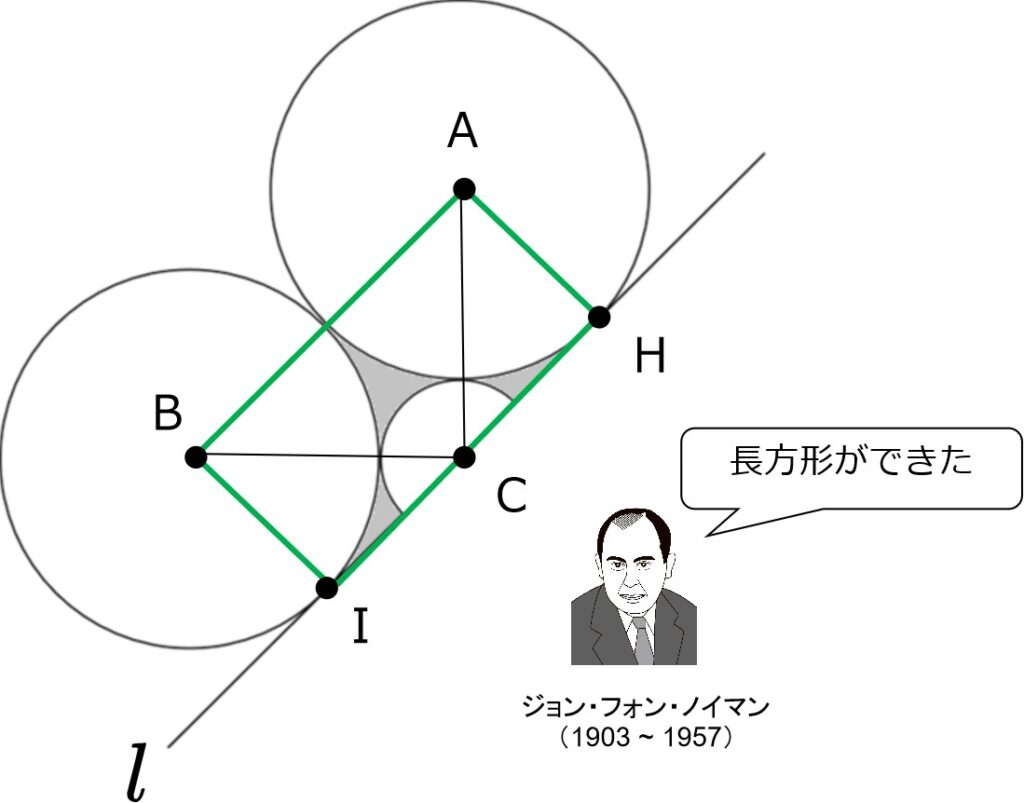
長方形ができました~(イェア−フッフゥ−)
この長方形の中をよく見ると、、、
おうぎ形と半円、それから灰色の領域に分けられます。
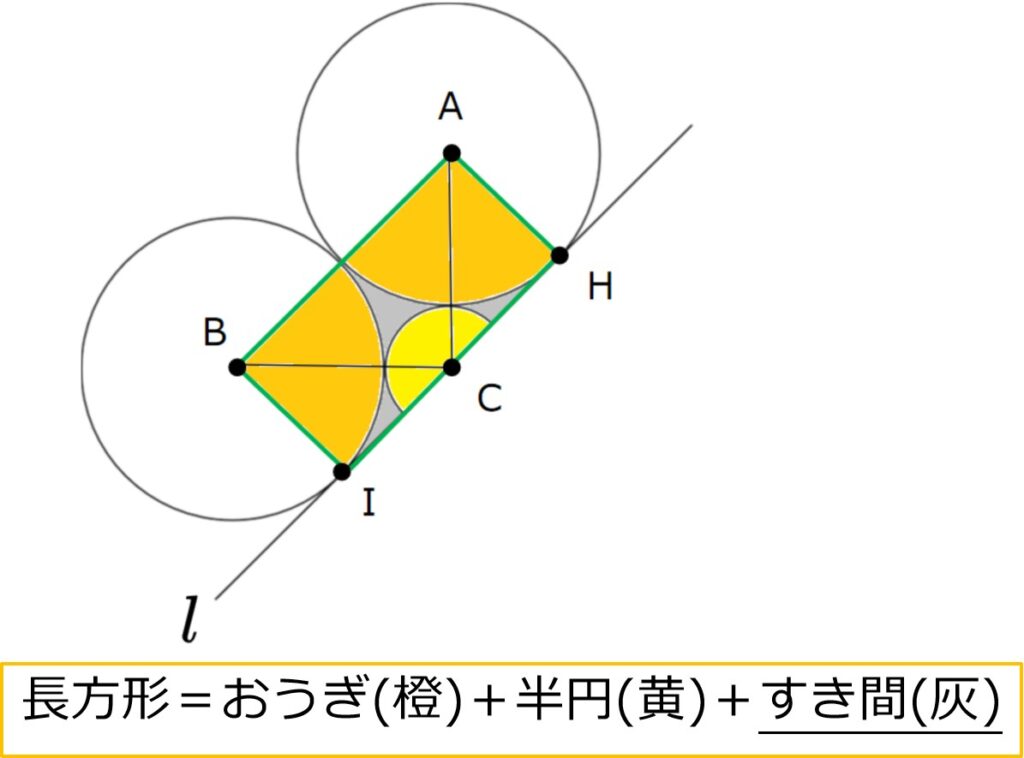

大きい円の半径が分かれば、公式で面積を求められそうね
円の半径は?→直角三角形を見つける
次は、半円の半径をどうやって求めるか、です。
実は、これも色分けした図に答えがあります。
図の直角三角形に注目。
半円の半径を\(r\)とすれば、
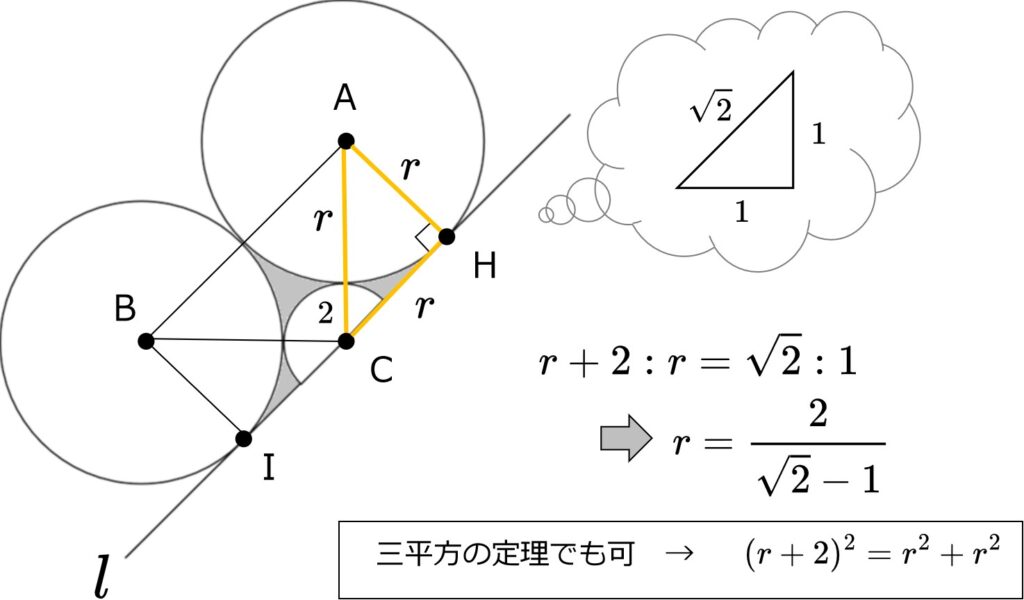
大きい円の半径が分かりました。
あとは、全体から余分なエリアを引けばOK。
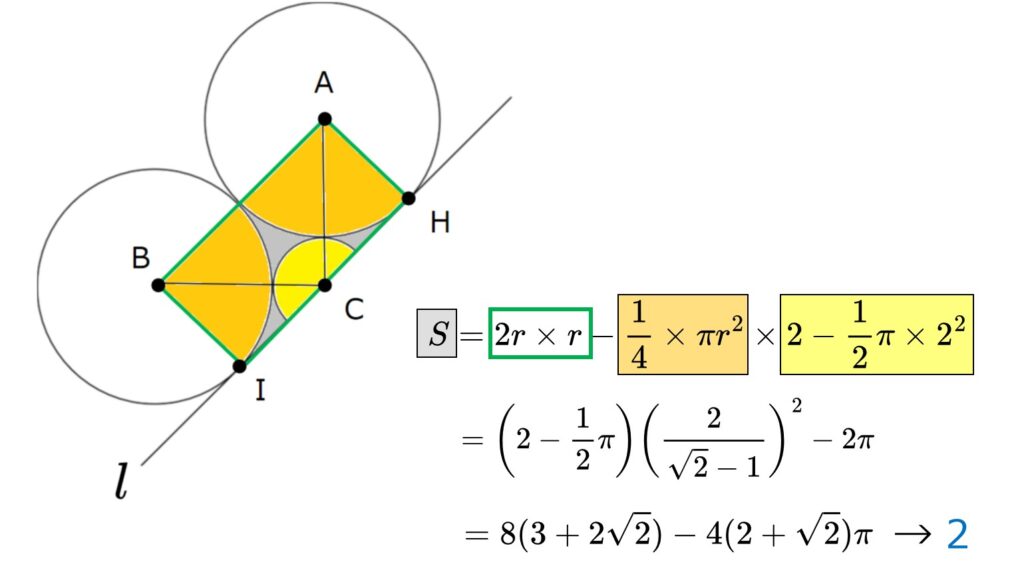
以上より、2が正解です。
おわりに:面積は「相似比か、公式か」
お疲れ様でした!
面積の問題は、
相似比か公式か
の見極めが肝心。
どちらのパターンかによって、注目すべきポイントは異なります。
必要な道具がそれぞれ異なるからです。

今回は公式を使うパターンでした
以下、参考。
「解法のポイント」について↓
「接線」がらみ↓
ちょっと有利な面積比の求め方↓
記憶保ったまま小学生に戻ったら背中にデスソースぬってYouTubeの王になる

そしてバタフライエフェクトでYouTubeが生まれない、と
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!






コメント