こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
迫りくるコロナの恐怖をものともせず、記事を投稿する生活。
前回はセレモニーに参加した男性のうち、単身だった者の人数を求める問題をやりましたね。
最初の一手が見えにくいタイプの問題です。
まだの方、国家総合職を狙うならぜひチャレンジしてみてください。
もう解いた方は、復習を忘れずに。
問題演習で数をこなすのはもちろん大切ですが、(解けなかった問題は特に)復習で深掘りするのも同じくらい重要です。
具体的には、一度解いた問題の解き直しをおすすめしています。
解説だけ読み返してサクッと済ませるのもいいですが、読むだけだとどうしても受け身の学習に終始してしまうので、やはり手を動かして能動的に学ぶスタイルが理想です。
もし解き直しで正答にたどり着かなくても、そこまで落ち込む必要はありません。
むしろ、ここでは間違えたり手詰まったりする箇所を明らかにすることが目的なので、成長のチャンスと捉えましょう。
間違えたら、「次は絶対に同じミスをしないぞ」という意気込みで解説を丁寧に読み返してみてください。
そうすることで、次に似た問題を見たときに解法を活用して自力で正答を導けるようになります。
これこそ、初見の問題に対応する力、「センス」なのではないかと思っております。
新しい問題にチャレンジするのと同じ熱量で復習にも取り組み、揺るぎない数的処理の「センス」を身に付けましょう。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
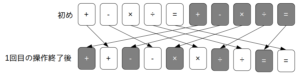
図のように、5つの算術記号(+ー×÷=)が書かれた白色および黒色のカードが横1列に並んでいる。このカードの並びに対し、次に示す「操作」を複数回行う。
操作:カードの並びを左右で5枚ずつに分け、左から「右半分の1枚目→左半分の1枚目→右半分の2枚目→左半分の2枚目→……」と交互に並べる
いま、図の「初め」の状態からスタートして、上述の操作を2022回繰り返したとき、「=が書かれた黒のカード」は左から何番目の位置にあるか。
- 左から5番目
- 左から6番目
- 左から7番目
- 左から8番目
- 左から9番目
3
カードを並べ替える操作を繰り返す問題です。
明らかに力技が通用しないので、工夫して調べる必要があります。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
この手の、極端に大きな回数の繰り返し操作がからむ問題は、変化の規則性を見出すことで解決できるケースがほとんどです。
実際に何回か操作を行ってみることで、何か規則性はないか、調べましょう。
試しに操作を5回行ってみます。

ここで「おや!」と気づいてほしい。
初めの状態と見比べると、5回目の結果はカードの並びが逆になってますね。
ということは、ここからあと5回同じ操作を繰り返せば、カードの並びは逆の逆で元通りになると考えられます。
ここから、操作を10回行うごとに並びがリセットされる、という規則性があることが分かります。
これさえ分かればあとは簡単です。
10回ごとに初めの並びに戻る、とは、10の倍数だけ繰り返すごとに初めの並びが再び現れる、ということです。
2022回繰り返す場合、2020回目に初めの並びが現れるので、そこからあと2回操作を行ったものが解答となります。
図の「2回目」の並びがそれにあたります。
これによると、「=が書かれた黒のカード」は左から7番目にありますね。
よって、3が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
規則性に基づき、並び替え操作の結果を論理的に推測する問題でした。
解説では10枚全てを並び替えてますが、訊かれているのはあくまで「=が書かれた黒のカード」の位置なので、そのカードにだけ注目して追跡するのも一つのやり方です。
本番では図も手書きしなければならないことを考えると、そのやり方の方が手を動かす労力が減る分、合理的かもしれません。
ただ、そうする場合は5回目の段階で並び順が逆になることには気づけないので、元に戻る10回目まで操作を書き出す必要が生じます。
ミスの無いように、自分のやりやすい解き方を身に付けましょう。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
題意の操作を5回繰り返した結果を次図に示す。

操作を5回繰り返したとき
この図から、題意の操作を5回繰り返すとカードの並びが逆転することが分かる。
よって、題意の操作を10回行うごとに、カードの並びは初めの状態に戻ると考えられる。
操作を2022回行った場合は、2020回目の操作で初めの状態が再現されるから、ここからあと2回操作を行えばよい。
その並びは上図の「2回目」に他ならず、このとき「=が書かれた黒のカード」は左から7番目にある。
よって、正解は3である。

コメント