こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「集合と論理」
まずは本サイトの肝である「解法のポイント」を紹介。
これで明日から1点アップ!?
- 命題として処理(対偶や三段論法)
- 真偽表を作る
- その他
この「解法のポイント」について、詳しく知りたい方は以下の記事をチェック。
ぶっちゃけて言うと、これだけでこの記事の半分はおしまい。
ほら、時間的な感覚だと人生の折り返しは20歳っていうし。

終了、解散!
ここからは、過去問をもとに作ったオリジナルの演習問題を解きながら、「解法のポイント」の使い方を学んでいきます。
演習問題:大陸にある国に関する推論
ある大陸のいくつかの国について、次のことが分かっているとき、論理的に正しいといえるのはどれか。
- 海に面していない国には、砂漠がある。
- 活火山のある国には、湖がある。
- 湖のある国には、海にも川にも面している。
- 砂漠のある国は、川に面していない。
- 砂漠のある国には、活火山がない。
- 活火山のない国は、海に面している。
- 海に面している国は、川に面している。
- 川に面している国には、湖がある。
- 湖がある国には、砂漠がある。
1
推論の正誤を問う問題。
2通りの解き方から、最適な方法を選んでください。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:条件命題から推論を導く
「論理的に正しい」というワードから、推論の問題と判断できます。
推論の正誤を問う問題の解き方は主に2パターンです。
- 命題として処理(対偶や三段論法)
- 真偽表を作る
- その他
本問は【1】の解き方が適しています。
【2】はオススメできません。
海/砂漠/活火山/湖/川の○×、計\(2^5=32\)通りを書き出すハメになるからです。

たかだか32通りなら、それほど無茶でもないけどね
条件を「ならば」式に命題化
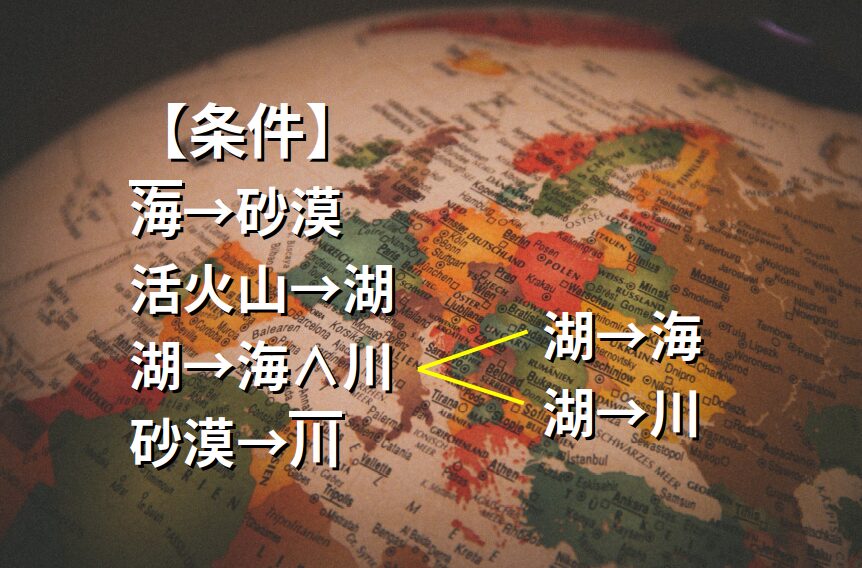
まずは条件文を「〜ならば…」の形式に読み替えて、命題化します。
\begin{align}
\overline{海} \Rightarrow 砂漠 \tag{i} \\
活火山 \Rightarrow 湖 \tag{ii} \\
湖 \Rightarrow 海 \land 川 \tag{iii} \\
砂漠 \Rightarrow \overline{川} \tag{iv} \\
\end{align}
(iii)は、次のように分割できます。
\begin{align}
湖 \Rightarrow 海 \tag{iii-a} \\
湖 \Rightarrow 川 \tag{iii-b}
\end{align}
以下、これらを使って選択肢の正誤を1つずつ検討します。
1→○:対偶と三段論法で推論を導く
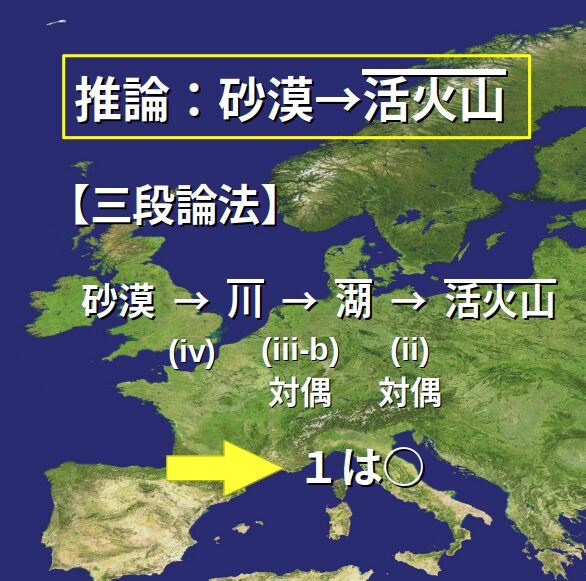
推論:\(砂漠 \Rightarrow \overline{活火山}\)
条件命題を使い、これを導き出せるか調べます。
「\(砂漠 \Rightarrow 〜\)」の形をもつのは、(iv)の「\(砂漠 \Rightarrow \overline{川}\)」。
ここに「\(\overline{川} \Rightarrow 〜\)」の形があれば、三段論法で次につながります。
「\(\overline{川} \Rightarrow 〜\)」の形を探すと……
(iii-b)の対偶が「\(\overline{川} \Rightarrow \overline{湖}\)」です。
よって、「\(砂漠 \Rightarrow \overline{川} \Rightarrow \overline{湖}\)」
次に、「\(\overline{湖} \Rightarrow 〜\)」の形を探します。
(ii)の対偶「\(\overline{湖} \Rightarrow \overline{活火山}\)」が見つかります。
これより、
\[
砂漠 \Rightarrow \overline{川} \Rightarrow \overline{湖} \Rightarrow \overline{活火山}
\]
このように、条件命題から推論が真であることを導けます。
よって、選択肢1は正しいといえます。
2→×:推論と同じ形の条件命題がない
推論:\(\overline{活火山} \Rightarrow 海\)
この推論を導くためには、「\(\overline{活火山} \Rightarrow 〜\)」の形の命題が必要です。
ところが、条件命題(&対偶)にこの形はありません。
よって、推論は確実に正しいとはいえず、選択肢2は誤りです。
3→×:同じく推論と同じ形がない
推論:\(海 \Rightarrow 川\)
これを導くには「\(海 \Rightarrow 〜\)」の形の命題が必要です。
しかし、条件命題(&対偶)にこの形はありません。
よって、推論は確実に正しいとはいえず、選択肢3は誤りです。
4→×:対偶を三段論法でつなげるけど…
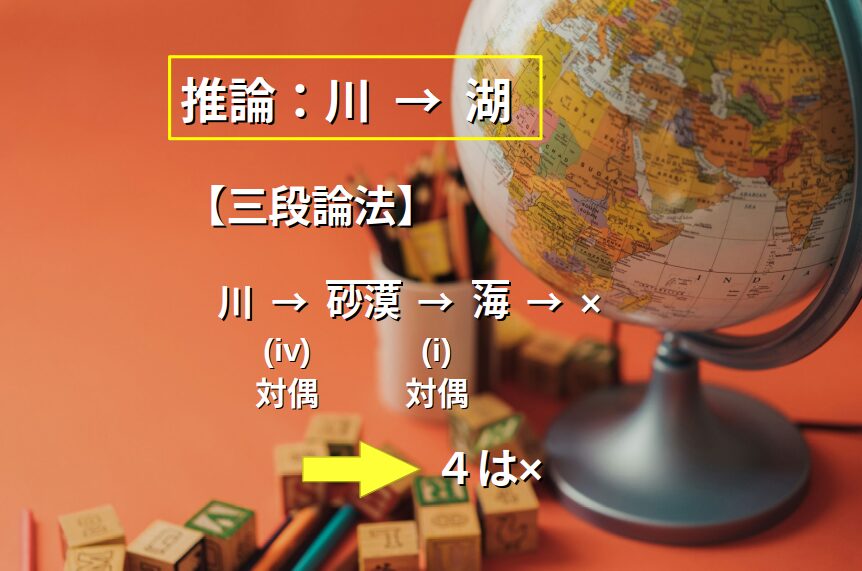
推論:\(川 \Rightarrow 湖\)
この推論を導くため、「\(川 \Rightarrow 〜\)」の形の命題を探します。
(iv)の対偶「\(川 \Rightarrow \overline{砂漠}\)」が見つかります。
次に、「\(\overline{砂漠} \Rightarrow 〜\)」の形をもつ命題を探します。
(i)の対偶が「\(\overline{砂漠} \Rightarrow 海\)」です。
三段論法でつなげると、「\(川 \Rightarrow \overline{砂漠} \Rightarrow 海\)」となります。
さらにつなげるには、「\(海 \Rightarrow 〜\)」の形の命題が必要。
ところが、条件命題(&対偶)にこの形はなく、先に進むことができません。
よって、推論は確実に正しいとはいえず、選択肢4は誤りです。
5→×:推論の「否定」命題を得る

推論:\(湖 \Rightarrow 砂漠\)
この推論を導くには、「\(湖 \Rightarrow 〜\)」の形の命題が必要。
(iii-a)「\(湖 \Rightarrow 海\)」および(iii-b)「\(湖 \Rightarrow 川\)」がそれです。
ここに、「\(海 \Rightarrow 〜\)」あるいは「\(川 \Rightarrow 〜\)」の形があれば次に進めます。
「\(海 \Rightarrow 〜\)」について、条件命題(&対偶)にこの形はありません。
「\(川 \Rightarrow 〜\)」については、(iv)の対偶「\(川 \Rightarrow \overline{砂漠}\)」が該当します。
これより、「\(湖 \Rightarrow 川 \Rightarrow \overline{砂漠}\)」となります。
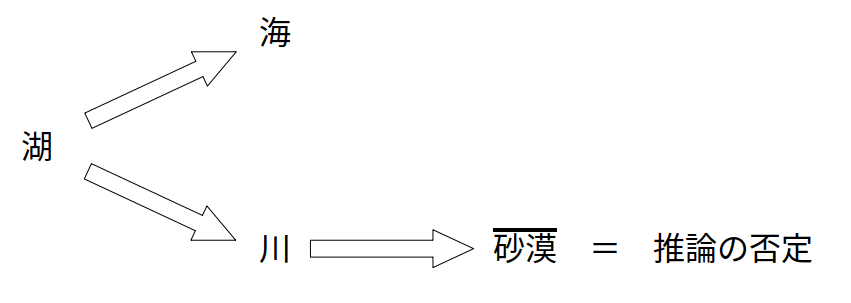
つまり「\(湖 \Rightarrow \overline{砂漠}\)」ですが、これは推論の否定命題に当たります。
よって推論は正しくなく、選択肢5は誤りです。
以上より、1が正解です。
おわりに:推論を命題化したら対偶と三段論法
お疲れ様でした!
推論の正誤を問う問題の解き方は、大きく2パターン。
【1】命題(対偶と三段論法)として処理する
または
【2】真偽表でしらみつぶし
推論問題を見たら、このどちらを使うのか?をまず考えてください。
今回は、大陸にある国の地形にまつわる推論を扱った問題でした。
条件を「〜ならば…」式に読み替えると、命題の問題として形式的に解くことができます。
対偶や三段論法を使い、推論(=選択肢)の正誤を明らかにします。
推論というゴールから、逆算的に命題をつなげていくのがミソ。
レトルトのビーフカレーに、刻んだサラダチキンをIN

ビーフカレーの尊厳も切り刻んでる
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
条件命題:
\begin{align}
\overline{海} \Rightarrow 砂漠 \tag{i} \\
活火山 \Rightarrow 湖 \tag{ii} \\
湖 \Rightarrow 海 \land 川 \tag{iii} \\
砂漠 \Rightarrow \overline{川} \tag{iv} \\
\end{align}
(iii)は、次のように分割できる。
\begin{align}
湖 \Rightarrow 海 \tag{iii-a} \\
湖 \Rightarrow 川 \tag{iii-b}
\end{align}
選択肢1→○
推論:\(砂漠 \Rightarrow \overline{活火山}\)
- (iv)「\(砂漠 \Rightarrow \overline{川}\)」
- (iii-b)の対偶「\(\overline{川} \Rightarrow \overline{湖}\)」
- (ii)の対偶「\(\overline{湖} \Rightarrow \overline{活火山}\)」
これらを三段論法でつなぐと、
\[
砂漠 \Rightarrow \overline{川} \Rightarrow \overline{湖} \Rightarrow \overline{活火山}
\]
これより、推論が真であることが示される。
ゆえに、選択肢1は正しい。
選択肢2→×
推論:\(\overline{活火山} \Rightarrow 海\)
条件命題(および対偶)に「\(\overline{活火山} \Rightarrow 〜\)」の形の命題がないため、三段論法で推論を導くことはできない。
ゆえに、選択肢2は誤り。
選択肢3→×
推論:\(海 \Rightarrow 川\)
条件命題(および対偶)に「\(海 \Rightarrow 〜\)」の形の命題がないため、三段論法で推論を導くことはできない。
ゆえに、選択肢3は誤り。
選択肢4→×
推論:\(川 \Rightarrow 湖\)
- (iv)の対偶「\(川 \Rightarrow \overline{砂漠}\)」
- (i)の対偶「\(\overline{砂漠} \Rightarrow 海\)」
これらを三段論法でつなげると、
\[
川 \Rightarrow \overline{砂漠} \Rightarrow 海
\]
ところが、条件命題(および対偶)に「\(海 \Rightarrow 〜\)」の形の命題がないため、ここから三段論法で推論を導くことはできない。
ゆえに、選択肢4は誤り。
選択肢5→×
推論:\(湖 \Rightarrow 砂漠\)
- (iii-b)「\(湖 \Rightarrow 川\)」
- (iv)の対偶「\(川 \Rightarrow \overline{砂漠}\)」
これらを三段論法でつなげると、
\[
湖 \Rightarrow 川 \Rightarrow \overline{砂漠}
\]
これは推論の否定命題にあたるため、推論は正しくない。
ゆえに、選択肢5は誤り。
よって、1が正解である。




コメント