こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
今回のテーマは「空間図形」です。
例年、1問は必ず出題されています。
おそらくこれは今後も変わらないでしょう。
そんな空間図形で頻出なのは、「断面」と「展開図」です。
これらの解き方は以下の記事で扱っているので、参考にどうぞ。
演習問題:切頂十二面体の面・頂点・辺の数
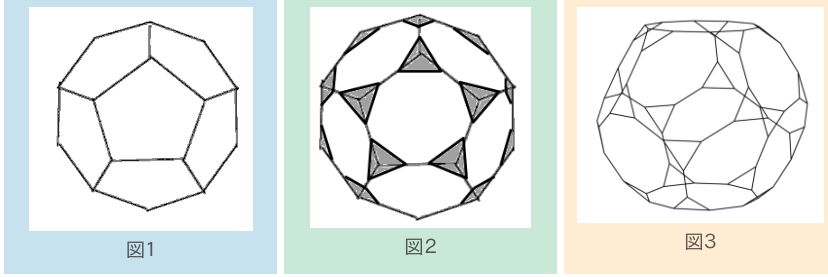
図1のような正十二面体の各辺を3等分し、図2に灰色で示した立体(正四面体)を全て取り除くと、図3のような多面体ができる。
図3に示す多面体の面・頂点・辺の数の組み合わせとして正しいのは次のうちどれか。
| 面 | 頂点 | 辺 | |
| 1. | 32 | 50 | 90 |
| 2. | 32 | 60 | 80 |
| 3. | 32 | 60 | 90 |
| 4. | 36 | 70 | 90 |
| 5. | 36 | 60 | 80 |
3
切頂十二面体と呼ばれる多面体の問題です。
公式を知らずに解くのは難しいでしょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説:正十二面体の面・頂点・辺を数えてから切り落とす
正十二面体の頂点を切り落としてできる立体は「切頂十二面体」といいます。
切り落とすことによる面・頂点・辺の増減は簡単に分かります。
そこで、まずもとの正十二面体の面・頂点・辺の数を求めてから、切り落としによる増減を加味することとします。
正十二面体の面・頂点・辺の数は?
最も簡単な方法は、数え上げること。
おあつらえ向きに、立体図が与えられているではありませんか。

よーし、図を見て、「1,2,3,4,…」
…裏側をイメージする段になって、筆者は諦めたようです。
正十二面体ともなると、いくら図が与えられているとはいえ、直接数え上げるのは困難です。

正八面体くらいだったら数え上げるのもアリなんだけどね
直接数え上げるのが無理なら、計算で求めるしかありません。
図によると、正十二面体は正五角形の面から成り立ってるのがヒント。
まず、面の数は言うまでもなく12です。
では頂点の数は?

5つの頂点をもつ面が12あるから、60?
うーん、当たらずとも遠からず。
12の面が合体して一つの頂点を共有するので、60よりも少なくなります。
正十二面体では3つの面が一つの頂点を共有するので、3で割った20が正しい頂点の数です。

要するに三位一体ってことよ(←よけい分からん)
辺の数も同じ考え方で分かります。
辺の場合、5×12=60ある辺が2つずつ重なって立体となるので、2で割って30が正しい数です。
ここまでをまとめると、正十二面体では、
面:12 頂点:20 辺:30
以上の求め方は一般にもよく知られた方法なので、これを「解法のポイント」としてまとめておきます。
- 面:\(n\)
- 辺:\(m×n÷2\)
- 頂点:\(m×n÷(一つの頂点を共有する面の数)\)
あとは、ここに頂点を切り落としたときの変化を加味するだけ。
一つの頂点を切り落としたときの変化を20の頂点に当てはめればOK。
切り落としによる面・頂点・辺の数の変化を20倍
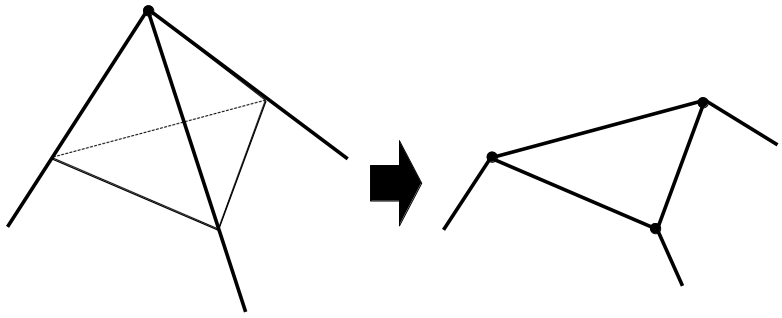
正十二面体の頂点を切り落とすことによる面・頂点・辺の数は次のように変化します。
面:+1
頂点:+2(1→3)
辺:+3
これと同じ変化が、頂点の数(=20)だけ起こるので、切頂十二面体の面・頂点・辺の数は次のように求められます。
面:12+1×20=32
頂点:20+2×20=60
辺:30+3×20=90
以上より、3が正解です。

ところどころ図の作りが粗いのは許してね
おわりに:正多面体の面・頂点・辺の数は公式で
お疲れ様でした!
今回は、切頂十二面体の面・頂点・辺の数を問う問題でした。
正多面体の面・頂点・辺の数はありがちなテーマなので、「解法のポイント」は覚えましょう。
丸暗記でもいいですが、「なぜそうなるのか」が重要です。

理屈を知ってればいつでも導出できるからね
なお、立体の図はいつも与えられるとは限らないので、正多面体の面の形は常識として知っておく必要があります。
最後にまとめておきます。
| 正四面体 | 正三角形 |
| 立方体 | 正方形 |
| 正八面体 | 正三角形 |
| 正十二面体 | 正五角形 |
| 正二十面体 | 正三角形 |
なんだろう、正”十二”面体の検索結果に正”二十”面体を混ぜるのやめてもらっていいですか
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
正十二面体の面・頂点・辺の数
面:12
頂点:5×12÷3=20
辺:5×12÷2=30
ここから一つの頂点を切り落とすと、面・頂点・辺の数の変化は、
面:+1
頂点:+2(1→3)
辺:+3

頂点の切り落としによる面・頂点・辺の増減
これが頂点の数(=20)だけ起こるから、切頂十二面体の面・頂点・辺の数は、
面:12+1×20=32
頂点:20+2×20=60
辺:30+3×20=90
以上より、3が正解である。

コメント