こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本ブログ、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、円形コースの周回で最初と同じ状況が再現されるための条件を考える問題でしたね。
今このタイミングで、解き方のポイントはどんなところだったかなーと思い出してみるだけでも、良い復習になりますよ!
バッチリだという方は、今日の問題に参りましょう。
本日の演習問題
無作為に選ばれた男女100名に対し行ったあるアンケート調査で、50歳未満の人は35人、50歳以上の人は65人であった。この100人の年収を調査したところ、次のア〜カの事実が判明した。
- 男性で年収が1000万円以上の人は、50歳未満および50歳以上のグループに少なくとも1人ずついる。
- 50歳以上の男性で、年収が1000万円未満の人は1000万円以上の人より30人多い。
- 年収が1000万円未満の男性で、50歳未満の人は50歳以上の人より20人少ない。
- 50歳未満の女性は19人である。
- 50歳未満の人のうち、女性で年収が1000万円未満の人は、年収が1000万円以上の男性より6人多い。
- 年収が1000万円未満の女性のうち、50歳未満の人と50歳以上の人の数の比は3:5である。
このとき、この100人において年収が1000万円未満の人と年収が1000万円以上の人の整数比として正しいのは、次のうちどれか。
- 7:3
- 3:2
- 4:1
- 67:33
- 37:13
1
「男女」とか「50歳未満/以上」というカテゴリが人数とともに与えられているので、集合に関する問題かな?と気づいてほしいところ。
条件の項目数が多いので、図を活用して情報を整理することも重要です。
以下、この問題の詳しい解説ですが、回りくどい説明が苦手な方は一番下の略解だけ読む、でも大丈夫です。
それではスタート!
詳しい解説
「男女」「50歳未満/以上」「年収1000円未満/以上」という3つのカテゴリがあり、例えば「50歳未満で年収1000万円未満の男性の人数が知りたい」というような場合、キャロル表が便利です。
キャロル表は慣れが必要ですが、本問のような問題で状況を整理するのに役立ってくれます。
3集合で人数を扱う場合はかなり有効なので、ぜひマスターしてくださいね。
さて、条件ア〜カのうち、まずキャロル表に記入できそうなのは、エの「50歳未満の女性は19人である。」ですね。これと問題文の「50歳未満の人は35人、50歳以上の人は65人」という部分を合わせて表に書き込むと、次のようになります。
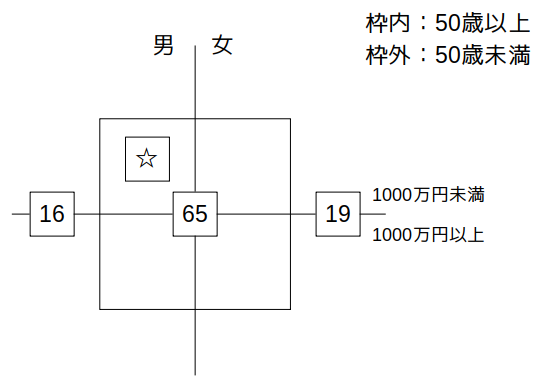
ここで、左端の「16」は、50歳未満の35人のうち、条件エの19人を引いて16人、ということです。
次に、キャロル表の問題では、どこかの領域の人数をとりあえず文字で置いてみると見通しが良くなることも多いです。
でも、どうせ文字を設定するなら、できるだけ多くの情報を可視化したいですよね。
そこで、条件ア〜カの中で言及された回数の多い領域の人数を\(x\)とおくこととしましょう。
ざっと見ると、イとウで「50歳以上で年収1000万円未満の男性」が2回登場してます。
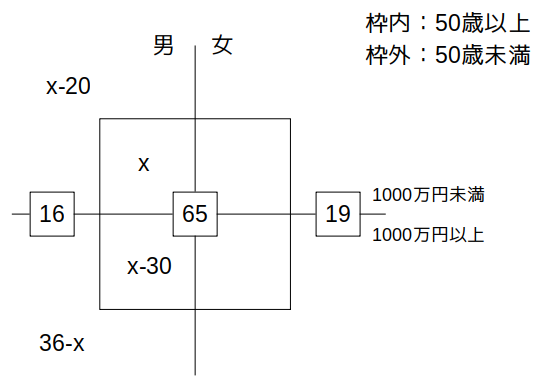
よって、50歳以上で年収1000万円未満の男性(☆印の領域)の人数を\(x\)とおくことにします。
すると、条件イより、50歳以上で年収1000万円以上の男性(\(x\)の真下の枠内)の人数が\(x-30\)となります。
また条件ウより、50歳未満で年収1000万円未満の男性(\(x\)の真上の枠外)の人数は\(x-20\)です。
さらに、50歳未満で年収1000万円以上の男性(\(x-30\)の真下の枠外)の人数が\(16-(x-20)=36-x\)であることも判明します。
ここまでをまとめたものを次図に示します。
これと条件オより、50歳未満で年収1000万円未満の女性は\((6-x)+6=12-x\)です。
\(12-x\)が明らかになったので、あとは50歳以上で年収1000万円未満の女性(\(x\)の右隣の枠内)の人数さえ分かれば、条件カが使えそうですね。
この際、その人数を\(y\)とおいて、\(y\)を\(x\)で表してみましょう。
こうすると、条件カより、\((42-x):y=3:5\)なので、\(y=70-\frac{5}{3}x\)
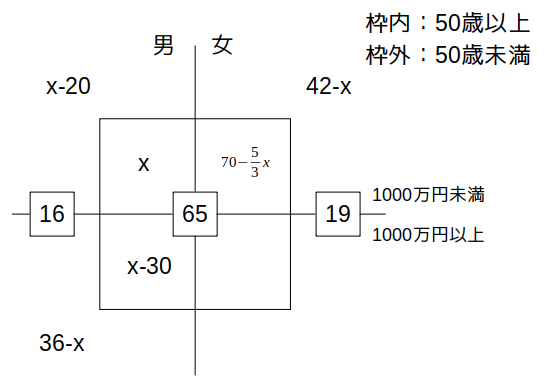
ここで、そもそも\(y\)は人数であったことを思い出しましょう。
そのためには\(\frac{5}{3}x\)が整数であることが必要なので、\(x\)は3の倍数でなければなりません。
ですが、これだけでは足りません。
何か、\(x\)の値を決定付けるヒントはないでしょうか?(\(x\)の取り得る値の範囲とか……)
問題文に戻りましょう。
与えられた条件の中で、まだ手を付けていないものがあったはずです。
それは何かというと、条件アです!
この条件を数式で表すと、\((x-30>0) \land (36-x>0)\)
すなわち、\(30<x<36\)
これが\(x\)の取り得る値の範囲になります。
この範囲にある3の倍数は「33」のみなので、\(x=33\)です。
こうして、以下のようにキャロル表の各領域の人数が確定します。
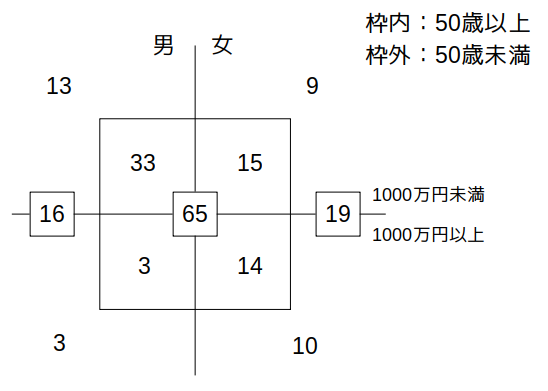
これより、「1000万円未満」:「1000万円以上」=70:30=7:3
よって、1が正解となります。
おわりに
お疲れ様でした!
いかがだったでしょうか?
3つのカテゴリがあって、そこに属する人の数が具体的に与えられている場合は、キャロル表を活用しましょう。
ベン図に比べるとキャロル表はマイナーで馴染みがないよ、という方は多いでしょう。
私も高校数学の集合分野はベン図だけで乗り切ったので、キャロル表は慣れるまでが大変でした汗
ですがしっかり練習すれば、今回のような問題にも活用できるレベルには到達できます。
今日の問題で、キャロル表の作成がうまくできなかった方は、これまでに勉強した参考書の例題をもう一度解き直してみてください。
繰り返しになりますが、解けない問題があった場合は、よりシンプルな設定の問題(=参考書にあるような問題)に戻ってみることが上達への近道です。
このサイトで紹介する問題たちは、どれも過去問に近い難易度なので、今解けなかったとしてもそこまで落ち込む必要はありません。(どちらかというと、その後の行動の方が大事ですよ)
解けない問題に出会ったときは、その問題を解くポイントは何であるかを明らかにして、同じカテゴリの易しい問題でそのポイントを徹底的に習得する、というプロセスが最適解なのかな、と思います。
今回の問題でいえば、「キャロル表」が解法のポイントだったので、つまづいた人はキャロル表の簡単な問題を復習するといいですよ!
本ブログでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
問題文の記述と条件エをキャロル表に記入すると以下のようになる。
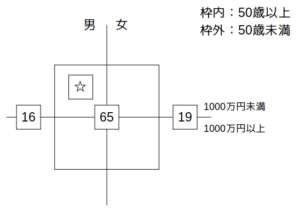
条件エをキャロル表に記入
なお、この図に示す通り、50歳未満の男性は\(35-19=16\)(人)である。
次に、50歳以上で年収1000万円未満の男性(☆印の領域)の人数を\(x\)とおく。
条件イより、50歳以上で年収1000万円以上の男性の人数は\(x-30\)(人)
条件ウより、50歳未満で年収1000万円未満の男性の人数は\(x-20\)(人)
さらに、50歳未満で年収1000万円以上の男性の人数は\(16-(x-20)=36-x\)(人)
これらをキャロル表に記入すると次図のようになる。
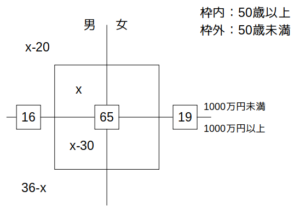
xの設定から分かること
すると、条件オより、50歳未満で年収1000万円未満の女性は\((6-x)+6=12-x\)(人)
ここで、50歳以上で年収1000万円未満の女性を\(y\)とおく。
条件カより、\((42-x):y=3:5\)なので、\(y=70-\frac{5}{3}x\)
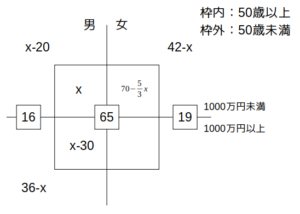
枠内の右上をxで表す
\(y\)は整数であることより、\(x\)は3の倍数である。
また、条件アより、\((x-30>0) \land (36-x>0)\)
すなわち、\(30<x<36\)
この条件を満たす3の倍数は33のみである。
よって、\(x=33\)
これより、キャロル表は次図の通りに決まる。
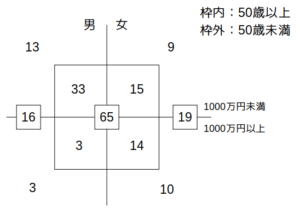
人数が確定
この表より、(1000万円未満):(1000万円以上)=70:30=7:3
よって、正解は1である。

コメント