こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、くじ引きの合計得点を推定する問題でした。
国家総合職ではおなじみ、対応関係が発展したような形の問題です。
「発展形」とはいっても、普通の対応関係と同じアプローチが通用します。
いい練習になる問題なので、解いてない方はぜひチャレンジしてみてください。
今回のテーマは「体積比」です。
空間図形は切り口に注目すると、平面図形の問題として処理できます。
平面図形に補助線を引くように、空間図形では適切な切り口で捉えましょう。
切り口については、以下の記事でも詳しく触れています。
演習問題:立方体と正四面体の体積比
1辺の長さが\(a\)である正六面体の体積は、1辺の長さが\(\sqrt{2}a\)である正四面体の体積の何倍か。
- \(\frac{\sqrt{6}}{2}\)倍
- \(\frac{8}{3}\)倍
- 3倍
- \(\frac{7\sqrt{3}}{3}\)倍
- 5倍
3
体積比の問題です。
ここでは2種類の解き方を紹介します。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
解法1:公式を使って体積を求めるやり方
正六面体(=立方体)と正四面体の体積をそれぞれ具体的に求めて比較します。
正六面体(=立方体)の体積が\(a^3\)であるのはいいとして、問題は正四面体の体積をどうやって求めるか、ですね。
これはよく知られたテーマなので、結果を丸暗記してもいいくらいなのですが、解き方を理解して記憶しましょう。

丸暗記が苦手な筆者はその都度計算してるよ
次図のように、正四面体の頂点Oから底面の△ABCへ下ろした垂線の足をPとします。
さらに、△ABCにおいて、頂点Aから辺BCへ下ろした垂線の足をDとします。
すると、点Pは線分AD上にあり、かつ△ABCの重心に一致します。
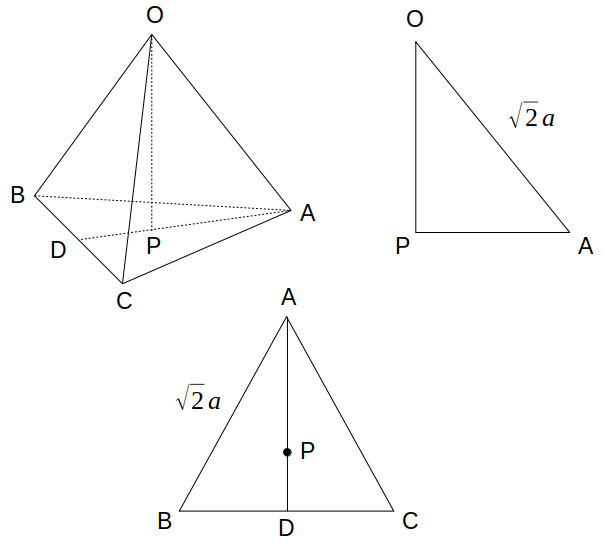
直角三角形ABDは、\(1:2:\sqrt{3}\)より、\(\mathrm{AD}=\frac{\sqrt{6}}{2}a\)
点Pは重心なので、\(\mathrm{AP}=\frac{2}{3}×\frac{\sqrt{6}}{2}a=\frac{\sqrt{6}}{3}a\)
これより、正四面体の高さが分かります。
直角三角形OAPに注目すると、三平方の定理が使えますね。
\(\mathrm{OP}=\sqrt{(\sqrt{2}a)^2-(\frac{\sqrt{6}}{3}a)^2}=\frac{2\sqrt{3}}{3}a\)

底面とか断面とか、平面の問題に持ち込むって考え方はすごく重要
適切な切り口を設定しよう
以上より、体積は、\(\frac{1}{3}×(\frac{1}{2}×\sqrt{2}a×\frac{\sqrt{6}}{2}a)×\frac{2\sqrt{3}}{3}a=\frac{a^3}{3}\)
つまり、立方体の体積は正四面体の体積の3倍であることが分かります。
よって、3が正解です。
平面図形の面積を徹底攻略シリーズ!第2回![終])
\\\【正五角形の面積比】///
第1回目に続き、図形の面積を攻略する問題の紹介です。
今回は相似比を利用するパターンの問題です。
第1回目の記事と併せて読めば、あなたも面積マスター!?
ぜひチャレンジしてみてください。
Twitterもよろしくね!↓
解法2:立体の埋め込みによる解き方
辺の長さが\(1:\sqrt{2}\)であることを利用すると、次図のように、立方体に正四面体をぴったり埋め込むことができます。
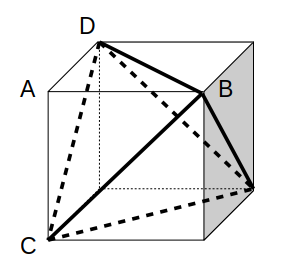
こうすると、正四面体の体積は、立方体から三角錐AーBCDを4個除くことで求められることが分かります。
三角錐AーBCDの体積は、というと、もとの立方体と比べて底面積が半分の錐体なので、
\(a^3×\frac{1}{2}×\frac{1}{3}=\frac{a^3}{6}\)
これより、正四面体の体積は、\(a^3-\frac{a^3}{6}×4=\frac{a^3}{3}\)
これは立方体の体積が正四面体の体積の3倍であることを示します。
よって、3が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
空間図形は、平面に落とし込んで考えるのが基本です。
立方体と正四面体の体積比に関する問題でした。
両者の体積を具体的に求める力技的な解法と、埋め込みを利用したちょっとスマートな解法、2つのやり方を紹介しました。
後者の方が圧倒的に速く解けますが、やや場当たり的で他の問題には応用しづらいですね。
前者の「力技」の方が学ぶところは多いので、教材という意味では優れているかもしれません。
正四面体の体積の求め方は定番のやり方なのでぜひ覚えましょう。
ちなみに、1辺の長さが\(a\)である正三角形の面積\(\frac{\sqrt{3}}{4}a^2\)と、正四面体の体積\(\frac{\sqrt{2}}{12}a^3\)あたりは暗記しておくとベターです。

どちらも、本問の解説で\(a→\frac{a}{\sqrt{2}}\)と置き換えたものだよ
最後に、同じく体積を扱った問題を紹介して終わります。
☆正四面体つながり、ただそれだけ。(解法のポイントあり)
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解

立方体に正四面体を埋め込む
図より、1辺の長さが\(\sqrt{2}a\)である正四面体の体積は、1辺の長さが\(a\)である立方体から三角錐AーBCDを4個分除くことで求められる。
三角錐AーBCDの体積は、もとの立方体に対して底面積が半分の錐体であることより、
\(a^3×\frac{1}{2}×\frac{1}{3}=\frac{a^3}{6}\)
これより、正四面体の体積は、\(a^3-\frac{a^3}{6}×4=\frac{a^3}{3}\)
よって、立方体の体積は正四面体の体積の3倍である。
したがって、3が正解である。


コメント