こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
今回のテーマは「空間図形」です。
センスがなければ解けない、と思われがちですが、基本を押さえれば対処できる問題もあります。
公務員試験では常連ともいえる分野なので、ちゃんと対策することをオススメします。

国家総合職なら、毎年1問は必ず出題されてるね
演習問題:立体のねじれ
図のように、同じ大きさの立方体を9つ組み合わせてできた立体がある。この立体を図の太線を含む平面で上下に切り分け、上側をA、下側をBとする。Aを固定したまま、Bを図の点線を軸として矢印の方向に90°だけ回転させたときにできる立体として正しいのは次のうちどれか。
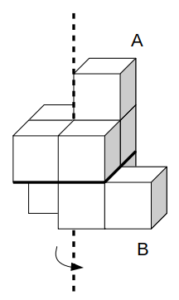
4
9つの立方体からなる立体の回転問題です。
頭の中で回転させるか、無理なら図を描いて回転後の立体がどんなものか把握する必要があります。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
回転を立体のままイメージしてみる
実際に90°回転させてみます。
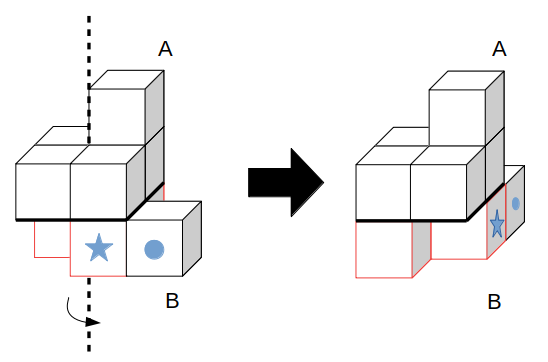
イメージしづらければ、一度にB全体を動かそうとするのではなく、立方体を軸回りに1個ずつ回転させて考えるのがオススメです。
本問なら、まず軸に接している3つ(図の赤い立方体)を1つずつ回転をさせると分かりやすいです。
赤3つの位置が分かったら、残りの1つ(●印)を★印の隣にくっつけて終了です。
切り口に注目する
立体のまま考えるのが難しければ、平面で考えるのもいいでしょう。
適切な切り口を設定しよう
切り口を考えるのは、空間図形では常套手段です。
切断面を捉えることの有用性は、以下の記事で語ってます。
解説に戻ります。
本問では、AとBの切り口の変化に注目します。

軸に垂直な平面で切るパターンのやつ
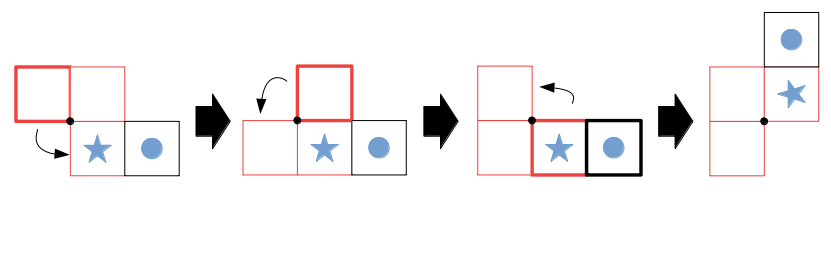
回転してできる立体が分かれば、あとは選択肢から同じものを選ぶだけです。
得意な方は、この段階でも答えが出せるでしょう。

立体がイメージできない、という方は消去法で絞り込む方法もあるよ
立体の特徴から消去法で絞り込む
特徴的な部分に注目し、当てはまらないものを除いていきましょう。
本問で重要なのは、できた立体には立方体が3つ並んだ部分が1つある、という点です。
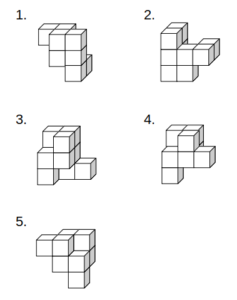
これに注目すると、まず「5」は除外できます。(3つ連続した部分がない)
そして、3つ並んだ部分が2箇所ある「2」も誤りであると判断できます。
「3」は、手前の立方体4つからなるテトリス(?)がBっぽいですが、奥の5つがAとは一致しないため誤りです。
「1」では逆に、左半分の5つがAに相当しますが右半分の4つがBとは一致しません。
「4」なら、左半分の4つがBに、右半分の5つがAにそれぞれ相当します。
正面から見て右に1回、奥に1回だけ転がすとできた立体に一致します。
よって、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
空間図形を平面(切り口)で捉えよう、という考え方は重要なテクニックの一つです。
立体の一部分を軸回りに回転させてできる図形として正しいものを選ぶ問題でした。
回転移動を考えるときは、小さい立方体に分割したり、切断面に注目したりと、単純化して扱う情報量を少なくすると分かりやすいです。
特に、後者はよく用いられるテクニックなので、ぜひマスターしてください。
空間図形はセンス、と思われがちですが、努力でカバーできる部分もあります。
今回紹介した「切り口に注目する」という考え方を身に付けるだけでも、空間図形の多くの問題に対応できるようになるはずです。
お手持ちの参考書にも載っているはずなので、難しかった方はこの機会に学び直してみましょう。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
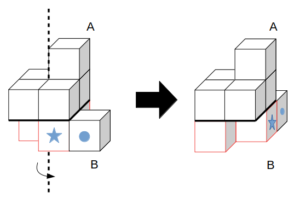
Bを軸回りに90°回転
これによると、できた立体には立方体が3つ連続した部分が1箇所ある。
よって、3つ連続した部分のない「5」は誤りである。
さらに、3つ連続した部分が2箇所ある「2」も誤りである。
また「3」は、手前の立方体4つがBに一致するが、奥の5つがAとは一致しないため誤り。
「1」は左半分の5つがAに相当するが右半分の4つがBとは一致しないため誤り。
したがって、4が正解である。

コメント