こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「ニュートン算」
「増えながら減る」関係を使って式を立てる文章題。
数量の変化が複雑でイメージしにくく、やっかいですよね。
苦手とする人も多いのではないでしょうか。

野菜でいうとピーマン(?)
だからこそ、ちゃんと勉強すれば周りに差をつけられます。
ニュートン算は解き方のパターンが決まっているからです。
本サイトでは、「解法のポイント」として過去に詳しく説明しています。
「文字でおく→方程式を立てる→連立で解く」
しかも、ニュートン算は、あるポイントに注目するともっと解きやすくなるんです。
キーワードは、
【収支に注目】
今回は、ニュートン算をもっと確実に解くために意識したいポイントを、数的処理の過去問みたいな演習問題を使って紹介します。

ガッツリ過去問レベルの内容です
演習問題:工場在庫の消化にかかる日数
1日に決まった数の製品を製造する工場において、場内にある製品の在庫を全て倉庫へ輸送する計画が立てられた。この工場は輸送用の車を2台(AとB)所有しており、1日あたりに輸送できる製品の個数は、Aは40個、Bは30個である。場内にある在庫を全て倉庫へ輸送するのに、Aのみを使った場合は60日、Bのみを使った場合は120日かかることが分かっている。当初はAとBを両方使い、ある日数で全ての在庫を輸送し終える計画であったが、途中でBが故障し5日間使用できなかったため、予定よりも多くの日数を要した。このとき、実際にかかった日数はいくらか。ただし、AとBが1日あたりに輸送できる製品の数はともに一定で、AとB以外の車を使うことはなかったものとする。
- 26日
- 27日
- 29日
- 31日
- 32日
2
工場の在庫を倉庫へ輸送する問題。
在庫を処理する間も、製品はどんどん作られています。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:補正ありのニュートン算
本問のゴールは、「実際にかかった日数はいくらか」を知ること。
そのためには何が必要でしょう?
かかった日数は「(在庫数)÷(1日に減る数)」で求められます。
もう少し掘り下げると、(1日に減る数)は「(AとBが1日に運ぶ数)ー(1日に作られる数)」のこと。
つまり、必要なのは以下の3つ。
・在庫数→不明
・AとBが1日に運ぶ数→Aは40個、Bは30個
・1日に作られる数→不明
「在庫数」と「1日に作られる数」を知ることが、第1の目標です。
以下、問題を細分化して考えます。
本問は、大きく前半と後半の2段に分けることができます。
【1】前半:「増えながら減る」はニュートン算
“1日に決まった数の製品を製造する工場において、場内にある製品の在庫を全て倉庫へ輸送する計画が立てられた。この工場は輸送用の車を2台(AとB)所有しており、1日あたりに輸送できる製品の個数は、Aは40個、Bは30個である。場内にある在庫を全て倉庫へ輸送するのに、Aのみを使った場合は60日、Bのみを使った場合は120日かかることが分かっている。”
製品を製造しながら、倉庫へ輸送する…
増えながら減る、です。

まさに、典型的なニュートン算
ニュートン算の「解法のポイント」を使います。
「文字でおく→方程式を立てる→連立で解く」
Step1:文字でおく
不明な数値を文字でおきます。
本問(の前半部)で、分からない数値を抽出しますと、
1日に作られる数→\(x\)
最初の在庫数→\(N\)
Step2:方程式を立てる
分かっている関係から、方程式を立てます。
本問では、「Aのみ」または「Bのみ」を使った場合にかかる日数を2通りに表し、=(イコール)で結びます。

ここで【収支に注目】の考え方を使う
まず、Aのみの場合について。
Aは毎日40個運びます。
同時に、工場では毎日\(x\)個作られます。
【収支に注目】すれば、在庫は毎日\(40-x\)個だけ減っていくことになります。
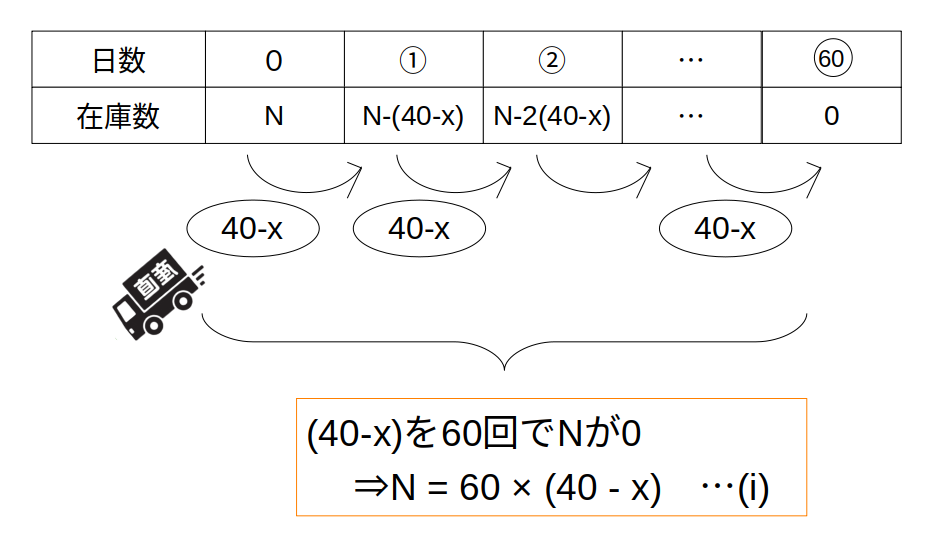
\(40-x\)を60日間(=60回)繰り返すと、\(N\)が0です。
つまり、
\[
N=60(40-x)……(\mathrm{i})
\]
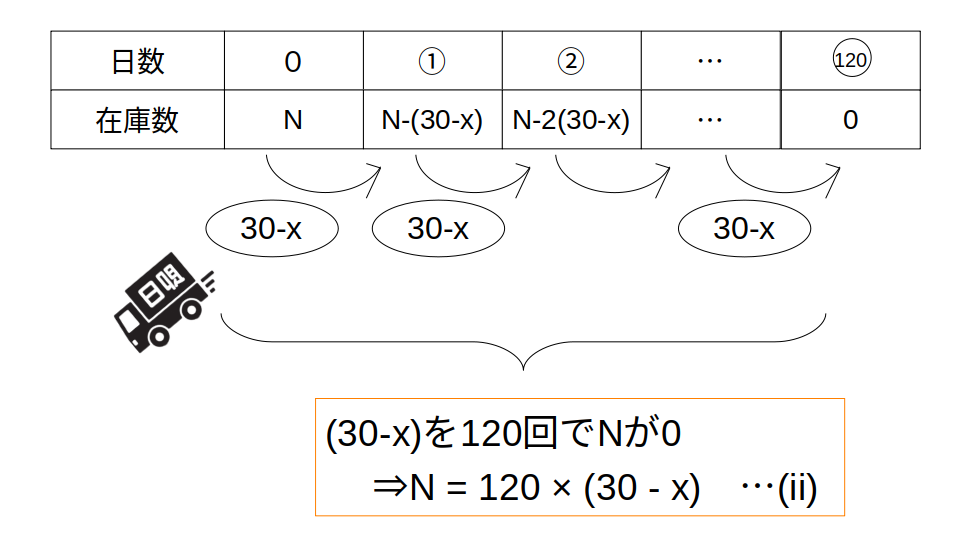
Bのみの場合も同じ。
Bが毎日30個運ぶ中、工場では\(x\)個作られます。
【収支に注目】すれば、在庫は毎日\(30-x\)だけ減ります。
全ての在庫がなくなるのに120日かかるので、
\[
N=120(30-x)……(\mathrm{ii})
\]
Step3:連立で解く
(i)と(ii)は、\(N\)と\(x\)の連立方程式。
解くと、\(N=1200\)、\(x=20\)
よくある「線分図」だと、こんな感じ↓
オレンジに注目した式が(i)、緑に注目した式が(ii)です。
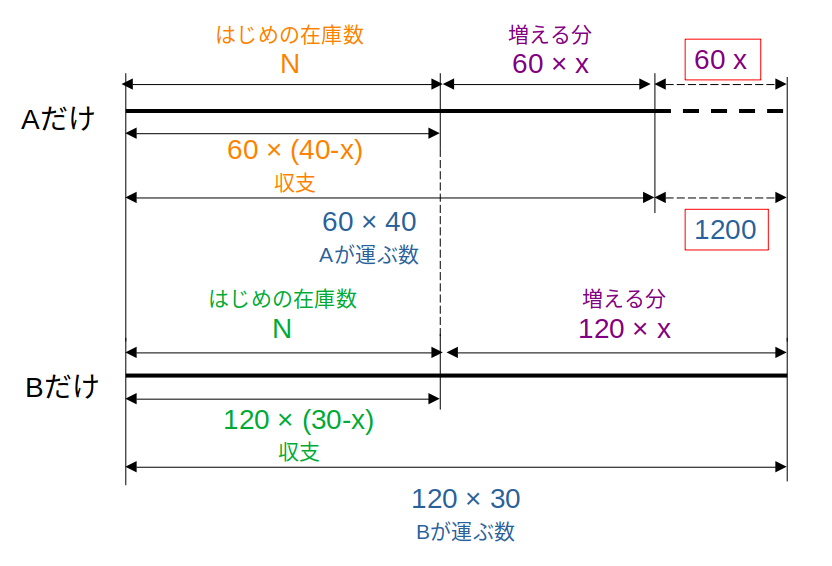

赤枠のイコールに注目するのが線分図でよくある解き方
【2】後半:積み残し分を補正
“当初はAとBを両方使い、ある日数で全ての在庫を輸送し終える計画であったが、途中でBが故障し5日間使用できなかったため、予定よりも多くの日数を要した”
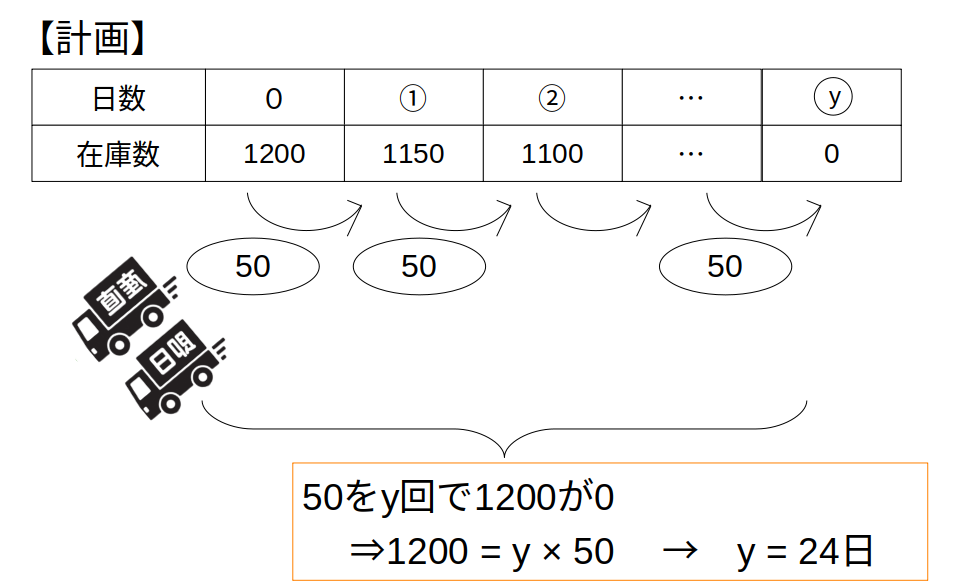
まず、「計画」について。
ここも【収支に注目】してみます。
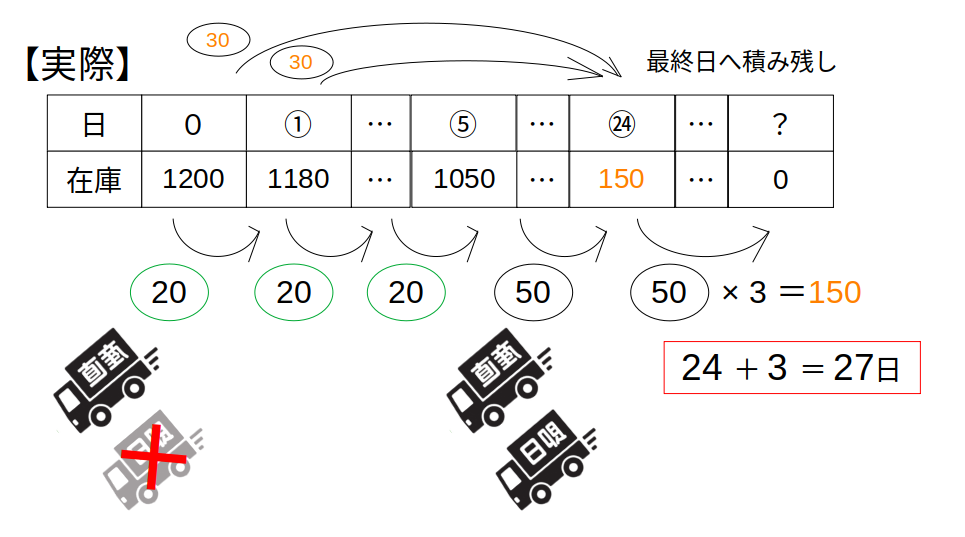
在庫が減るペースは、毎日\((40+30)-x=50\)個
毎日50個ずつ減っていくと、在庫が0になるのは、1200÷50=24日後
これが当初の計画です。
では、実際はどうだったかというと…
“途中でBが故障し5日間使用できなかった”
とあります。
この5日間に運ぶはずだった30×5=150個が、積み残しとして最終日(24日目)に残ります。
この150個を消化するために、「予定よりも多くの日数を要した」わけです。

Bが壊れた日はいつであっても問題ナシ
AとBで運ぶ場合、在庫が減るペースは1日あたり50台。
ということは、積み残しの消化にかかる時間は、150÷50=3日
これより、実際にかかった日数は24+3=27日…(答)

前半みたいに「N+150=50×(日数)」としてもOK
以上より、2が正解です。
おわりに:ニュートン算は「収支」に注目
お疲れ様でした!
ニュートン算は、【収支に注目】すると解きやすくなります。
この考え方の良い点は、議論がシンプルになること。
解説でも、「増えながら減る」が「減る」だけに変わってましたよね。
増える分を差し引いて(40-\(x\))おけば、単に減っていくだけの問題になります。

「増えて減って、つまりどれだけ変化するの?」が重要
今回は、在庫を作りながら輸送する、という問題でした。
ニュートン算は、「文字→方程式→連立」の流れが基本。
まずはコレを使えるように練習しましょう。
その上で【収支に注目】するやり方を身につければ、正答率がアップしますよ。
オマケのもう1問↓
なんか会社で、来年のイベント係(飲み会とか主催するやつ)に任命されてた

次回「会社の飲み会絶対断るマン(筆者)、敗れる」
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
前半:
・在庫数→\(N\)
・AとBが1日に運ぶ数→Aは40個、Bは30個
・1日に作られる数→\(x\)
Aのみの場合、在庫は毎日\(40-x\)個ずつ減る。
すると、在庫が全てなくなるのにかかる日数は、
\[
N=60(40-x)……(\mathrm{i})
\]

Aのみの日数を式にする
Bのみの場合、在庫は毎日\(30-x\)個ずつ減る。
すると、在庫が全てなくなるのにかかる日数は、
\[
N=120(30-x)……(\mathrm{ii})
\]

Bのみの日数を式にする
(i)と(ii)を連立させて解くと、
\(N=1200\)、\(x=20\)
後半:
在庫が減るペースは、毎日\((40+30)-x=50\)個
在庫が0になるのは、1200÷50=24日後(計画)
「途中でBが故障し5日間使用できなかった」について。
この間、Bが運ぶはずであった30×5=150台が、24日後へ持ち越される。

実際は積み残し消化に+3日
これを消化するのに要する日数は、150÷50=3日
したがって、実際にかかった日数は、24+3=27日…(答)
以上より、2が正解である。




コメント