こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「方程式」
まずは本サイトの肝である「解法のポイント」を紹介。
これで明日から1点アップ!?
- 未知数を文字でおく
- 数量の関係を式にする
- 連立させて解く
この「解法のポイント」について、詳しく知りたい方は以下の記事をチェック。
ぶっちゃけて言うと、これだけでこの記事の半分はおしまい。
ほら、時間的な感覚だと人生の折り返しは20歳っていうし。

終了、解散!
ここからは、過去問をもとに作ったオリジナルの演習問題を解きながら、「解法のポイント」の使い方を学んでいきます。
演習問題:砲丸投げで持ち点を競うゲームと方程式
A、B、Cの3人は、砲丸投げの記録で得点を競うゲームを行った。A、B、Cは、はじめにある2桁の整数が持ち点として与えられ、砲丸投げの記録を計4回競った。1回ごとに記録を比較し、1位だった者は、他の2人からそれぞれ自分の持ち点と同数の得点を受け取った。ゲームの結果および持ち点について、次のことが分かっているとき、はじめにBが持っていた持ち点はいくらか。
ただし、各回いずれも1位の者はただ1人のみであったとする。
- 1回目はBが1位であった。
- 2回目と3回目はともにAが1位であった。
- 4回目はCが1位で、AとBはCに持ち点を与えた結果、持ち点がちょうど0点になった。
- Aのはじめの持ち点は30点以下であった。
- 13点
- 19点
- 26点
- 32点
- 39点
1
4回の砲丸投げで持ち点を競う問題。
求めたいのは「はじめにBが持っていた持ち点」なので……?
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:方程式を解いたら整数問題
数的処理で箇条書きの条件といえば、文章題(対応関係/位置関係/順序関係)です。
条件から確実に正しいといえる文を選ぶ、というやつ。
本問も、箇条書きの条件が与えられてますが、文章題ではありません。
本問の選択肢は、文ではなく「数値(持ち点)」だからです。
持ち点という数値を求める、というのが本問の目的であり、ゴールです。
これを明確にしておくのは大切。
目的がはっきりすると、方針を立てやすくなるからです。
カーナビでルートを調べるときも、最初に目的地を入力しますよね。
ゴールを意識するからこそ、そこへ至る道筋が見えてきます。

最近のゲームは「次何するか」を教えてくれる親切設計
数値を求める方法として一番ポピュラーなのが、「方程式」です。
そこで、本問も方程式で解決できないか、と考えてみます。
方程式の「解法のポイント」の出番です。
- 未知数を文字でおく
- 数量の関係を式にする
- 連立させて解く
以下、この手順に沿って解いていきます。
求めるものを文字でおく
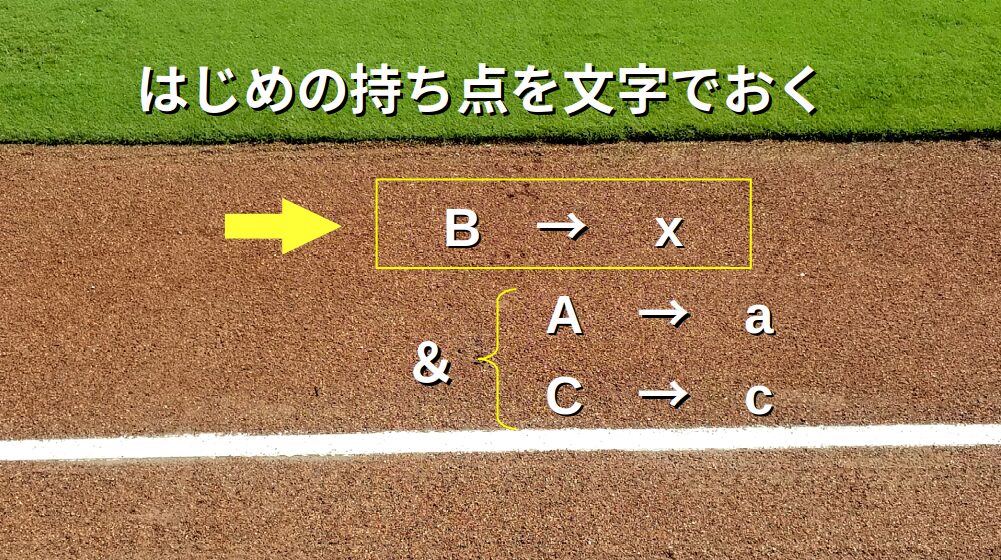
求めたい数値を\(x\)でおくのがキホン。
本問では、「はじめにBが持っていた持ち点」を\(x\)とします。
しかし、これだけでは方程式の立てようがありません。
本問は、Bだけでなく、AとCの持ち点も調べる必要があります。
そこで、AとCのはじめの持ち点も、それぞれ\(a, c\)とおきます。

3つ目の条件がAとCの持ち点に言及してるのもヒント
A〜Cの各回の持ち点を、次のような表に整理します。
| はじめ | 1回目 | 2回目 | 3回目 | 4回目 | |
| 1位 | ー | B | A | A | C |
| A | \(a\) | ||||
| B | \(x\) | ||||
| C | \(c\) |
表には
各回の1位・1回目はBが1位であった。
・2回目と3回目はともにAが1位であった。
・4回目はCが1位で、AとBはCに持ち点を与えた結果、持ち点がちょうど0点になった。
と、はじめの持ち点を書き込んであります。
持ち点を文字式で表す
ここから、 ゲームのルール1位だった者は、他の2人からそれぞれ自分の持ち点と同数の得点を受け取った にしたがって各回の持ち点を文字式で表していきます。
例えば、1回目はBが1位なので、BはAとCから\(x\)ずつ受け取った結果、持ち点が\(3x\)になります。
AとCは\(x\)ずつ減って、持ち点はそれぞれ\(a-x\)および\(c-x\)です。
| はじめ | 1回目 | 2回目 | 3回目 | 4回目 | |
| 1位 | ー | B | A | A | C |
| A | \(a\) | \(a-x\) | |||
| B | \(x\) | \(3x\) | |||
| C | \(c\) | \(c-x\) |
同じように、各回の持ち点を文字式で表します。
| はじめ | 1回目 | 2回目 | 3回目 | 4回目 | |
| 1位 | ー | B | A | A | C |
| A | \(a\) | \(a-x\) | \(3(a-x)\) | \(9(a-x)\) | \(13a-c-12x\) |
| B | \(x\) | \(3x\) | \(4x-a\) | \(7x-4a\) | \(4x-c\) |
| C | \(c\) | \(c-x\) | \(c-a\) | \(c-4a+3x\) | \(3(c-4a+3x)\) |
条件で方程式を立てて解く

4回目の結果に 3つ目の条件の後半〜で、AとBはCに持ち点を与えた結果、持ち点がちょうど0点になった。 を当てはめると、方程式が2つ立てられます。
Aの持ち点がちょうど0点
→\(13a-c-12x=0\)
Bの持ち点がちょうど0点
→\(4x-c=0\)
→\(c=4x\)
Aの式に代入すると、\(13a-16x=0\)
これを\(a\)について解きます。
\[
a=\frac{16}{13}x……(☆)
\]
整数の候補を挙げてしらみつぶし

ここで、「\(a\)は整数である」という大前提を思い出しましょう。
(☆)が整数であるためには、\(x\)が「13の倍数」であることが必要です。
すると、\(x=13, 26, 39, ……\)
(☆)より、\(x\)と\(a\)の対応は次の通りです。
| \(x\) | 13 | 26 | 39 | … | 91 |
| \(a\) | 16 | 32 | 48 | … | 112 |

\(x\)は2桁の整数だから91が最大
このうち、
4つ目の条件Aのはじめの持ち点は30点以下であった。
を満たすのは
\(x=13, a=16\)
のみ。
よって、1が正解です。
おわりに:文字でおいて方程式を立て、解く
お疲れ様でした!
求める対象が具体的な数値である場合は、方程式で解決できる可能性があります。
求めたいものを\(x\)とおき、方程式を立てて解く、という流れが基本です。
今回は、増減する持ち点を文字でおく方程式の問題でした。
前半で方程式を立てて解き、後半は整数問題として処理します。
未知数3つに対し、得られる方程式は2つ。
ここに「整数である」という条件が加わると、未知数を具体的に求められます。
ちなみに、候補を挙げてしらみつぶし、という解き方は整数問題で頻出です。

整数問題の「解法のポイント」も思い出してほしい
- 範囲を絞る
- 倍数、約数、余りから候補を書き出す
- しらみつぶしで特定
夏、夕立のあと、湿った匂い

タモさん「雨降った?」
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
はじめにBが持っていた持ち点を\(x\)とおき、各回の得点を次のような表にする。
| はじめ | 1回目 | 2回目 | 3回目 | 4回目 | |
| 1位 | ー | B | A | A | C |
| A | \(a\) | ||||
| B | \(x\) | ||||
| C | \(c\) |
ゲームのルール「1位だった者は、他の2人からそれぞれ自分の持ち点と同数の得点を受け取った」にしたがい、各回の持ち点を文字式で表すと、次表の通りになる。
| はじめ | 1回目 | 2回目 | 3回目 | 4回目 | |
| 1位 | ー | B | A | A | C |
| A | \(a\) | \(a-x\) | \(3(a-x)\) | \(9(a-x)\) | \(13a-c-12x\) |
| B | \(x\) | \(3x\) | \(4x-a\) | \(7x-4a\) | \(4x-c\) |
| C | \(c\) | \(c-x\) | \(c-a\) | \(c-4a+3x\) | \(3(c-4a+3x)\) |
3つ目の条件の後半「〜で、AとBはCに持ち点を与えた結果、持ち点がちょうど0点になった。」を当てはめると、次の2式を得る。
\(13a-c-12x=0\)
\(4x-c=0\)
→\(c=4x\)
Aの式で、\(c\)を消去し\(a\)について解く。
\[
a=\frac{16}{13}x……(☆)
\]
(☆)において、\(a\)が整数であるためには、\(x\)が「13の倍数」であることが必要となる。
つまり、\(x=13, 26, 39, ……\)
\(x\)と\(a\)の対応は次表の通りとなる。
| \(x\) | 13 | 26 | 39 | … | 91 |
| \(a\) | 16 | 32 | 48 | … | 112 |
このうち、4つ目の条件「Aのはじめの持ち点は30点以下であった。」を満たすのは
\(x=13, a=16\)のみ。
よって、1が正解である。




コメント