こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
先日、ようやく一人暮らしを始めたのに、郵便物の転送がうまくできず、今日は実家に届いてしまった郵便物を取りに帰っていました。
晴れて実家を出たのに、早々にとんぼ返りする羽目になるとは……
明日にでも郵便局へ行って、小一時間問い詰めて来ることにしよう。
それはそれとして、
前回は、立体図形の各辺を一筆書きで描けるか否かを判断する問題をやりました。
解法の大まかな流れは思い出せますか?
忘れてしまった方は、この機会にもう一度復習しましょう。
数的処理に限らず、知識は時間が経てば経つほど忘れてしまうので、解いた後少し時間をおいてからまた思い出す、ということを習慣付けると定着しやすくなるのでおすすめです!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
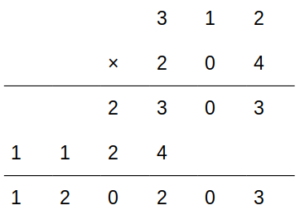
以下は、5進法で表されたある2つの整数を乗じた結果を筆算により求めたものである。A〜Eには、それぞれ0〜4のうち異なる整数が1つずつ当てはまるものとする。このとき、A+B+Eの値を5進法で表したものとして適切なのは次のうちどれか。
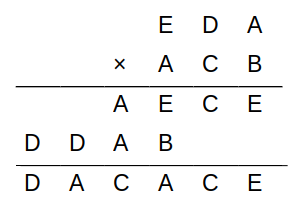
- 11
- 12
- 13
- 14
- 20
4
5進法のかけ算がテーマの問題です。
筆算の結果を見て、A〜Eに当てはまる整数を推測します。
解答に必要な数字はAとBとEだけですが、結局は全ての整数を明らかにすることになりそうですね。
以下、この問題の詳しい解説になります。
長ったらしい説明はいらないよ、という方は一番下に略解をまとめてあるので、そちらまで読み飛ばしていただいても問題ありません。
それではスタート!
詳しい解説
筆算の結果を見て、何か違和感を感じませんか?
そうです、計算過程の「2段目」がないんです。
3桁×3桁の筆算であれば、普通は真ん中の段も3段になるはずですよね。
それが本問では2段しかありません。
どうしてかな?という疑問を持つところが、この問題のスタートラインです。
…別に出題ミスではありませんよ笑
普通は3段になるはずのところが2段しかないのは、2段目が全て0で省略されてしまった結果なんです。
「A×C」も、「D×C」も、「E×C」も、全てが0、ということです。
これは「C=0」だからに他なりませんね。
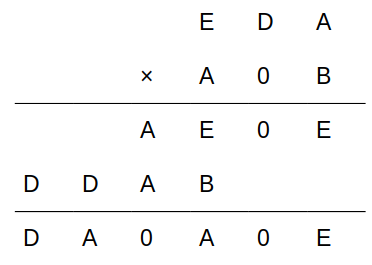
次に、A×Dの一の位がAである(=下から2段目の2桁目)ことに注目します。
結論からいうと、これより「D=1」が分かるのですが、理由は以下の通りです。
仮にD≠1とします。
このとき、A=1とすると、A×Dの一の位はDとなってしまうので不適です。
よってA≠1ですが、残りの整数(2〜4)のうちから異なる2つの整数を選ぶとしても、
(A×Dの一の位)=Aとなる組み合わせは存在しません。(実際に計算してみると分かります)
これにより、「D=1」であることが分かります。
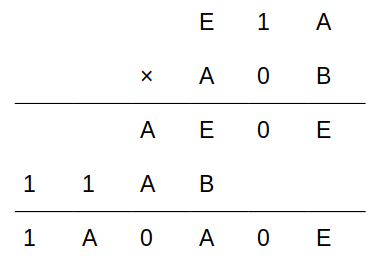
今度は、結果の5桁目がAであること、および(A+Aの一の位)=0、に着目します。
Aは2か3か4のいずれかですが、A+Aからの繰り上がりは0または1しかありません。
(最大の4+4でも繰り上がりは1)
A+Aの繰り上がりが0であるとすると、A=1となってしまいD=1に矛盾します。
これよりA+Aの繰り上がりは1で、A=1+1=2、とすれば辻褄が合います。
(2+2=4では繰り上がりは0ですが、そこに前の桁E+Bからの繰り上がりがあったと考えられます)
よって、「A=2」と決まります。
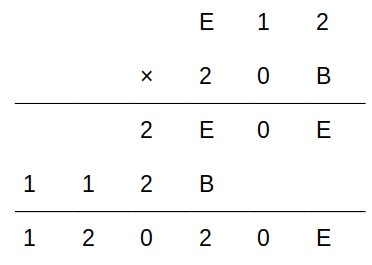
あとはBとEはそれぞれ3か4のいずれかですが、2×2=B(下から2段目の1桁目)なので「B=4」であり、残りは「E=3」と決まります。
これにより、以下のように筆算の数字が確定します。
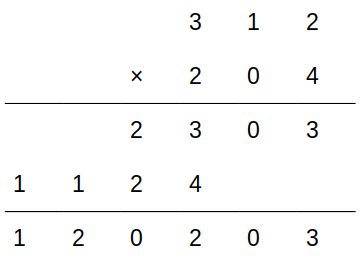
実際に計算してみると、ちゃんと矛盾がないことも確かめられます。
よって、A+B+E=2+4+3=9(10進法)→14(5進法)なので、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
n進法をテーマにした覆面算の問題でした。
n進法の考え方を知っていれば、あとは筆算から分かることを紐解いていくだけになります。
これまで数的処理の勉強をしてきた方なら、2進法や16進法あたりは見たことがあるでしょう。
2進法であれば2カウントごとに1つ繰り上がるし、16進法であれば16カウントごとに1つ繰り上がるのでしたね。
5進法であっても、それは同じです。
難しいことを覚える必要はありません。
5カウントごとに1つ繰り上がる、という規則さえ分かっていれば本問は解けてしまいます。
とはいえ、冒頭からはっきりと「5進法」というワードが出ているので、n進法がどうしても苦手だ、という方は本試験であればスルーするのもアリだと思います。
本番まで時間のある方はしっかりと勉強しておくことをおすすめしますが、そうでない方は問題を取捨選択する覚悟も必要となってきます。
教養試験は満点を取るテストではないので、完璧主義はかえってアダとなってしまいます。
このサイトで勉強するときも、見た瞬間に「捨てる問題なのか?解くべき問題なのか?」を見極める練習をすると良いでしょう。
問題を見て、瞬時に捨てる判断ができれば、その分他の問題に使える時間が増えることになるので、教養試験全体の得点がアップしますよ!
本番まで時間がない方は、「問題の見極め」もぜひ視野に入れてみてください。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
筆算の過程において、中段の2段目が省略されていることより、C=0
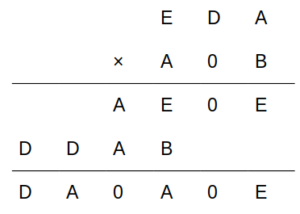
C=0を記入
次に、A×Dの一の位がAである(=下から2段目の2桁目)ことにおいて、D≠1と仮定する。
このとき、A=1とすると、A×Dの一の位はDとなってしまうので不適。
よってA≠1
しかし、残りの整数(2〜4)のうちからどの異なる2つの整数AとDを選んだとしても、
(A×Dの一の位)=Aとなる組み合わせは存在しない。
したがって、D=1
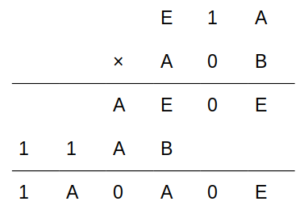
D=1を記入
ここで、結果の5桁目がAであること、および(A+Aの一の位)=0、に注目する。
Aは2か3か4のいずれかなので、A+Aからの繰り上がりは0または1である。
A+Aの繰り上がりが0であるとすると、A=1となりD=1に矛盾する。
よってA+Aの繰り上がりは1で、A=1+1=2
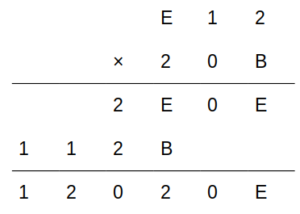
A=2を記入
下から2段目の1桁目の計算において、2×2=Bより、B=4
よって、残りはE=3
B=4とE=3を記入
以上より、A+B+E=2+4+3=9(10進法)→14(5進法)
よって、正解は4である。

コメント