こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、9つの立方体からなる立体をねじる問題でした。
空間図形の基礎的な解法を紹介しています。
ぜひ解いてみてください。
もう解いた方は、お疲れ様でした。
忘れないうちに、ぜひとも復習をしましょう。
復習では、類似の問題に活用することを念頭に置きながら解法を学んでみてください。
教材となる問題は、多くの場合は過去の試験で使われてしまったものです。
とすると、同様の問題が再び出題される確率は極めて低いので、個々の解法を丸暗記しても場当たり的にしかならないのです。
あくまで「似たような」問題に対応できるような勉強をすべきでしょう。
本サイトの「解法のポイント」は、似た傾向の問題にすぐ活用できる形に知識をまとめたものです。
忙しい場合はこれだけを見返すのもオススメです。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
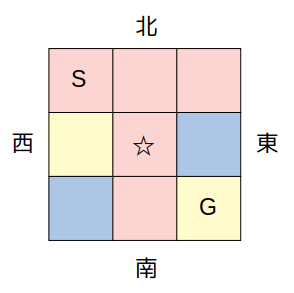
図のように、縦3マス×横3マスの計9マスを3色に色分けし、スタート地点Sとゴール地点Gを設定したシートがある。いま、このシート上を動く駒に計4つの指示を与え、SからGまで移動させるゲームを行う。駒に与える指示は、次のa〜eから無作為に選ばれる。
a:現在のマスが赤色のとき、南に1マス移動
b:現在のマスが赤色のとき、東に1マス移動
c:現在のマスが青色または黄色のとき、東に1マス移動
d:隣接する青色のマスに移動
e:隣接する黄色のマスに移動
このとき、Sから図の☆を経由してGにたどり着く確率はいくらか。ただし、「隣接する」とは、マス同士が4辺のいずれかで接している状態を表すものとし、一度選ばれた指示が再度実行されることはないものとする。
- \(\frac{3}{10}\)
- \(\frac{2}{5}\)
- \(\frac{5}{9}\)
- \(\frac{4}{7}\)
- \(\frac{2}{3}\)
4
駒の移動に関する確率の問題です。
指示の出し方は全部で\({}_5 P_4\)=120通りですが、ゴールにたどり着くルートだけ考えれば十分です。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
4回の指示(=移動)でゴールへ行くのは、最短ルートを進んだ場合です。
指示の出し方は、単純に計算すると全部で\({}_5 P_4\)=120通りあります。
しかし、これはあくまで単純計算で、この120通りには移動が成立しないパターンも含まれます。
例えば、Sは赤なので、1つ目の指示が「c」であるパターンは除外されます。
さらに、Sが隣り合うマスは赤と黄色のみなので、1つ目の指示が「d」となることもありません。
つまり、1つ目の指示としてあり得るのはa、b、eのいずれかです。
以降も同じように、移動先によって出せる指示は限定されてきます。
結局は一つ一つの変化を丁寧に追って、可能なパターンを列挙するしかないことに気づくでしょう。
分岐をたどるには樹形図が便利です。
本問で可能な指示のパターンを樹形図で書き出すと、次のようになります。
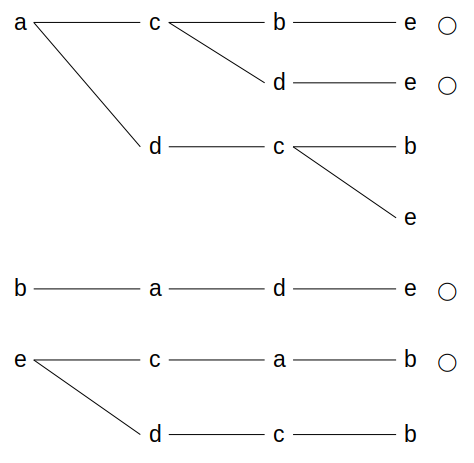
移動の過程で☆を経由するものには○を付けました。
指示が無作為に(=等しい確率で)選ばれるとすれば、確率の母数は図の7通りです。
このうち、☆を経由するルートは4通りなので、その確率は\(\frac{4}{7}\)に他なりません。
よって、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
盤上の駒が特定のマスを経由してゴールにたどり着く確率を考える問題でした。
ゴールにたどり着くパターンだけ考えればよいことに気づけば、全通りを列挙するという発想にも至ります。
ゴールまでの最短経路はせいぜい4通りしかない、というところからも類推できるかもしれません。
最初の指示がaかbかeのどれかしかない、という点にいち早く着目して、しらみ潰しの解き方に舵を切ってもらいたいところです。
手早く、かつ正確に駒の移動のし方を全て把握しましょう。
お手持ちの参考書にも載っているはずなので、難しかった方はこの機会に学び直してみましょう。
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
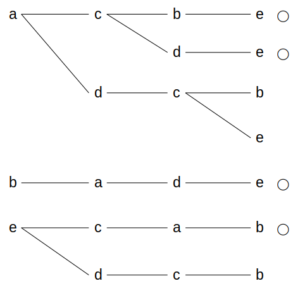
指示の出し方の全パターン
全7通りの移動方法のうち、☆を通過するパターン(=○印)は4通りである。
よって確率は\(\frac{4}{7}\)
したがって、4が正解である。

コメント