こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、団体注文の割引率を求める問題でしたね。
どんな解き方だったか忘れてしまったという方は、ぜひ一度戻って確認してみてください。
数的処理に限らず、一度解いた問題は時間を空けずに復習するのが定着のコツですよ!
大丈夫な方は、本日の問題に進みましょう。
本日の演習問題
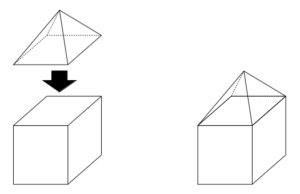
一辺の長さが1である立方体と、同じく一辺の長さが1の正方形を底面に持つ四角すいを、下図のように正方形をのりしろとして接着することを考える。いくつかの四角すいを用いることにより、一筆書きで全ての辺をなぞることが可能な立体ができる場合がある。そのような立体の形状が、少なくとも1つ存在するときに用いられる四角すいの数として、正しいものはどれか。
- 2個
- 6個
- 2個または4個
- 2個または6個
- 4個または6個
4
このサイトでは久しぶりの図形問題です。
テーマは一筆書きですが、平面ではなく立体図形なのがこの問題の大きな特徴ですね。
以下でこの問題を詳しく解説します。
長ったらしい説明が嫌な方は一番下に略解をまとめてあるので、そちらまで読み飛ばしていただいても問題ありません。
それではスタート!
詳しい解説
選択肢を見るに、四角すいが偶数個の場合だけ考えれば十分ですね。
選択肢をヒントとして利用しようという考え方は、以前の記事でも取り上げたことがあります。
まだ見てない方は、よかったらご覧ください↓
経費が最小となるミーティング会場|数的処理の穴場
一筆書きが可能な条件としては、以下の2つが知られています。
- 奇点が0個である(=偶点のみ)
- 奇点が2個だけある
これらのいずれかを満たす図形は、一筆書きが可能となります。
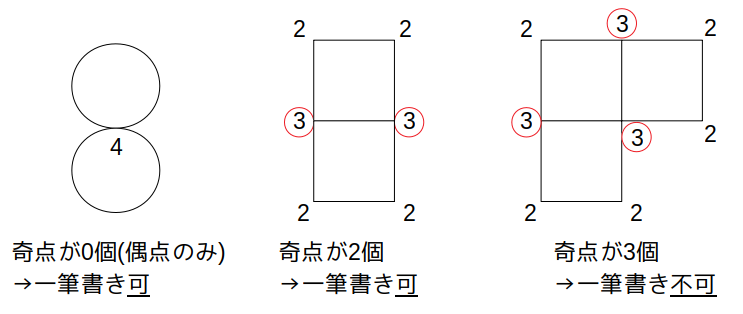
よって本問では、四角すいをくっつけてできる立体の各頂点の奇偶を調べるのが主な方針となります。
以下、四角すいを何個使うかによって、次の(i)〜(iii)の3通りに場合分けします。
- 四角すいを2個使う場合
- 四角すいを4個使う場合
- 四角すいを6個使う場合
(i)四角すいを2個使う場合
対称性より、四角すいのくっつけ方は次の2通りに限られます。
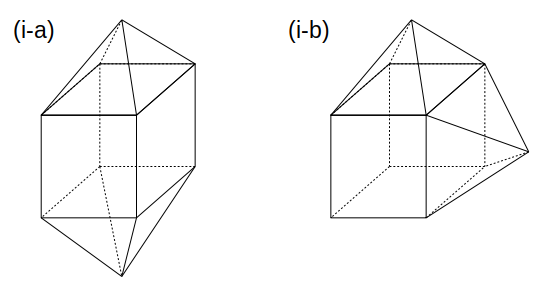
立体図で直接数えてもOKですが、説明の都合と今後のために、位相図を使った解き方を覚えましょう。
位相図の考え方は「補足」として末尾に説明を載せるので、苦手な方はそちらをご参考ください。
ここでは、実際に位相図を活用して問題を解いていきたいと思います。
まず、(i-a)および(i-b)の位相図を描くと、次図のようになります。
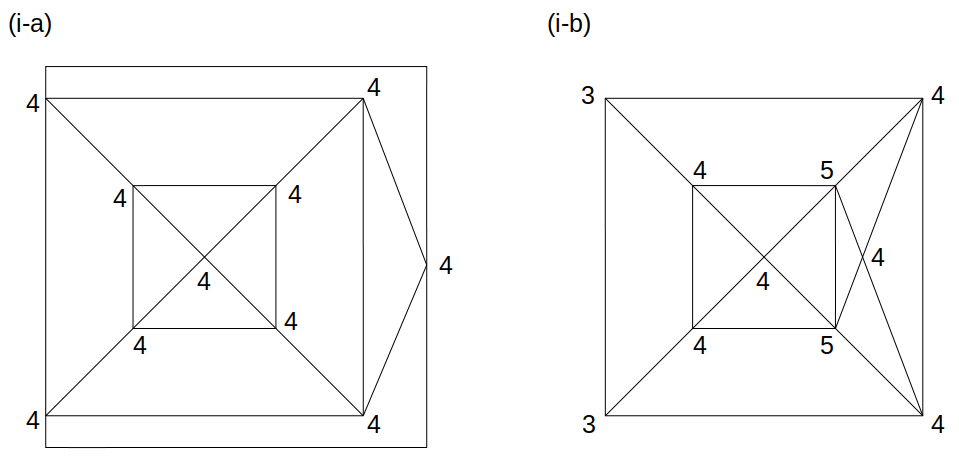
(i-a)では奇点が0個なので一筆書きが可能ですが、(i-b)では奇点が4個なので一筆書きは不可能です。
題意は「(一筆書きが可能な)立体の形状が、少なくとも1つ存在するときに用いられる四角すいの数」なので、このケースは一筆書きが可能、という結論になります。
(ii)四角すいを4個使う場合
対称性を考えると、四角すいのくっつけ方は以下の2通りに限られます。
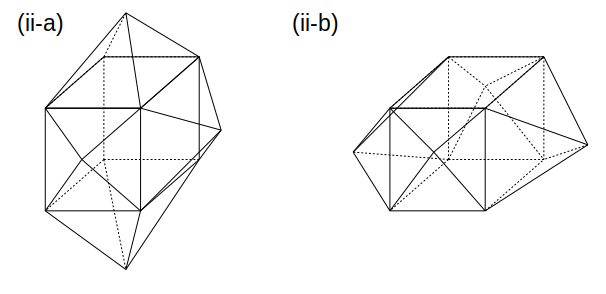
これらの位相図を描くと次のようになります。
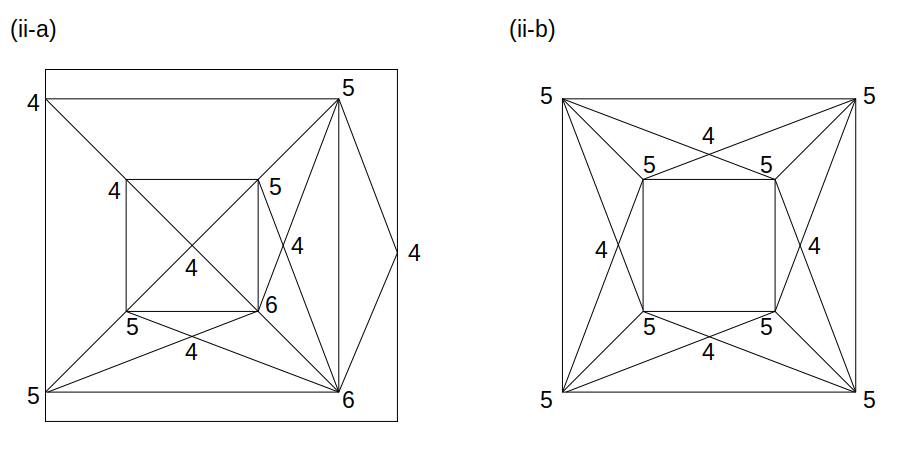
各頂点から出る経路数もこの図の通りで、奇点の数を数えると、(ii-a)は4個、(ii-b)は8個なのでいずれも一筆書きはできません。
よって、四角すいが4個の場合は一筆書きが不可能、となります。
(iii)四角すいを6個使う場合
これは立方体の全ての面に四角すいがくっついた場合になります。
立体図と位相図は次のようになります。
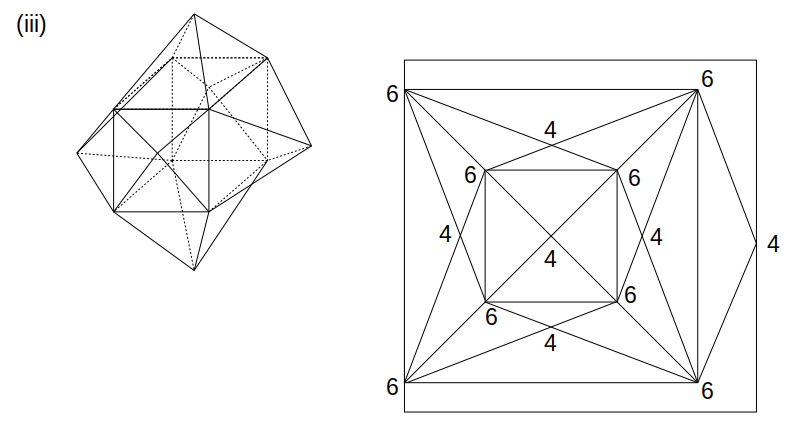
この図に示す通り、各頂点は全て偶点となっているので、一筆書きできます。
よって、四角すいが6個の場合は一筆書きが可能、となります。
以上から、一筆書きが可能なのは四角すいが6個の場合で、4が正解となります。
補足:位相図の考え方
位相図は簡単に言うと、真上から見た図を末広がりに引き伸ばしてできる図です。
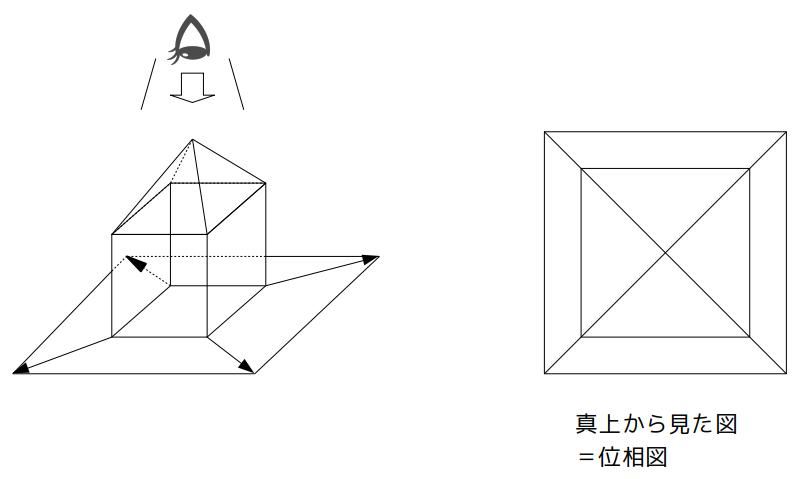
底面に近くなるほど大きくゆがんでしまってますが、頂点どうしのつながりは元の立体から保たれているので、奇点か偶点かを調べる目的ならこれでOKです。
(i-a)のように、下側にも四角すいがくっついているケースは少し複雑ですが、次図のように頂点を右に移動させてから、頂点同士のつながりを復活させるイメージです。
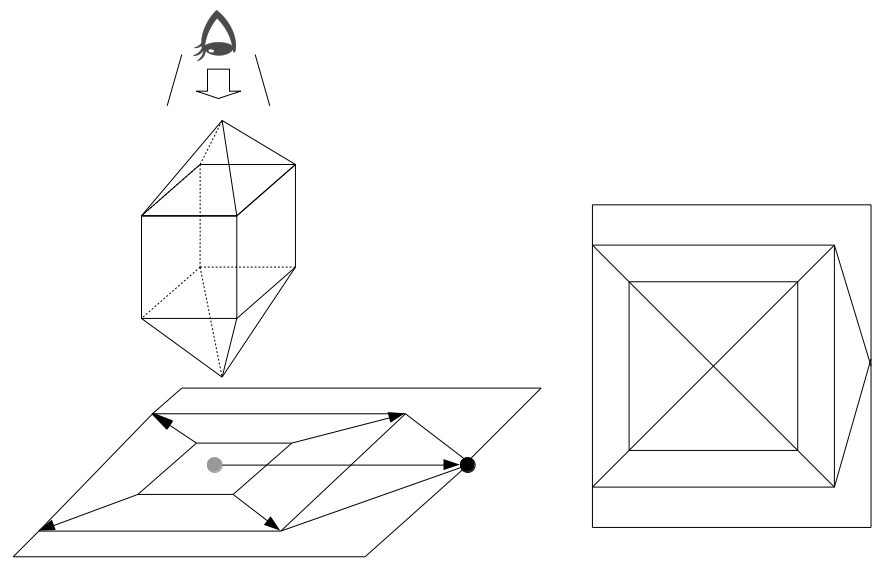
位相図を導入することで、立体図の頂点を結ぶ経路を平面的に議論することができるようになります。
おわりに
お疲れ様でした!
いかがだったでしょうか?
一筆書きの問題では、位相図を使って考えるのが基本的な解法です。
できあがった立体図をイメージできて、かつ正確な図が描ければ立体図のまま考えるのもアリですが、四角すいの数が多くなってくるとなかなか難しくなってきます。(私はムリでした……)
そんな方のために、今回は位相図を使った解説を紹介しました。
位相をテーマにした問題は国家総合職では時折出題されるので、この機会に位相図の書き方をマスターしてしまいましょう!
位相図のイメージは、立体を真上からプレスした様子を表した図、と捉えてもいいかもしれません。
前項の「補足」も活用しながら、自分なりの理解でいいので、立体図→位相図の変換をスムーズに行えるようになるまで練習しましょう。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
選択肢より、四角すいが偶数個の場合を調べれば十分であると分かる。
よって以下では、四角すいの個数で場合分けし、位相図を描いて奇点の数を調べる。
立体の対称性より、図形は次の2通りに限られる。
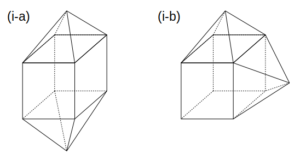
四角すいが2個の場合
これらを位相図にすると次図のようになる。
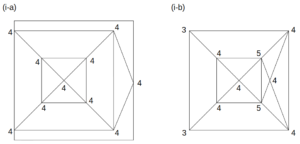
四角すいが2個の場合の位相図
この図に示す通り、(i-a)の立体は偶点のみで一筆書きが可能であるが、(i-b)の立体は奇点が4個で一筆書きが不可能であるから、このケースは「一筆書きが可能なケース」に該当する。
立体の対称性より、図形は次の2通りに限られる。
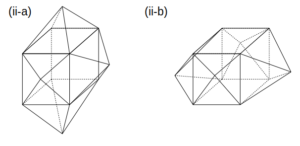
四角すいが4個の場合
これらを位相図にすると次図のようになる。
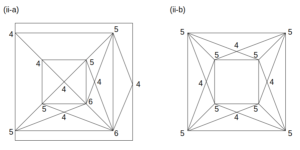
四角すいが4個の場合の位相図
この図に示す通り、奇点の数は(ii-a)の場合で4個、(ii-b)の場合8個であるから、ともに一筆書きは不可能で、このケースは不適。
(ii)四角すいを6個使う場合
立方体の全ての面に四角すいが付くから、立体図および位相図は次図のようになる。
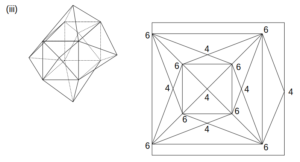
四角すいが6個の場合の立体図と位相図
この図に示す通り、各頂点は全て偶点なので、一筆書きが可能である。
以上から、正解は4である。

コメント
i-bは一筆書き不能と思いますがいかがでしょうか?
ご指摘ありがとうございます。
こちらで確認したところ、i-bの経路数のカウントにミスがありました…
おっしゃる通り、(i-a)が○でも(i-b)が×なので、(i)のケースは不適、ということになりますね。
最終的な解答を含めて修正したので、ご確認ください。
今後とも、本サイトをどうぞご贔屓に。
問題文の主旨は「一筆書きができる立体において、使用している四角錐の数はいくつか?」なので、四角錐2つも対象としてカウントすべきではないかと。
なので回答は3だと思います。
以下、問題文から抜粋
一筆書きで全ての辺をなぞることが可能な立体ができる場合がある。そのような立体ができるときに用いられる四角すいの数
ご意見ありがとうございます。
再度検討しましたが、問題文の表現が少し紛らわしいようでした。お詫びいたします。
おっしゃることは尤もで、
「(一筆書きで全ての辺をなぞることが可能な)立体ができるときに用いられる四角すいの数」
=「一筆書きができる形状が一つでもあれば○」
というのが正しい解釈でしたね。
これより、四角すいが2個のケースは○で、これに四角すい6個の場合が加わり、正解は4となります。
(3は「2個と4個」ですが、4個の場合は2パターンとも一筆書きが不可能なので、×です)
ご不明な点あればコメントください。
今後とも本サイトをどうぞよろしくお願いいたします。