こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
「バイオフィリア」といって、自然とのふれあいを求める本能が人間にはあるそうです。
自然に触れることでこの「バイオフィリア」が満たされると、睡眠の質が向上したりストレスが解消されるなどのメリットがあるそうですが、中でも集中力がアップするという情報は、このサイトで勉強される皆さんには耳よりなのではないでしょうか?
出かけるのが億劫でも、自然を感じられる画像や音声だけでも効果があるそうなので、ぜひ積極的に取り入れたいですね。

この記事を書きながら筆者は延々と自然の音を聞いてるよ
今回のテーマは「面積」です。
実は、面積の求め方は2通りしかありません。
以下の記事に詳しく書いているので、まだ見てない方はぜひ覗いてみてください。
演習問題:正六角形と面積
次図において、灰色で示される領域の面積はいくらか。ただし、正六角形ABCDEFの面積を1とする。また、点G、H、Iはそれぞれ辺BC、DE、FAの中点である。
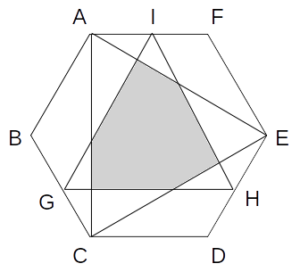
- \(\frac{1}{3}\)
- \(\frac{3}{7}\)
- \(\frac{3}{10}\)
- \(\frac{5}{16}\)
- \(\frac{5}{21}\)
4
正六角形を題材にした平面図形の問題です。
平面図形といえば補助線ですが、どんな線を引くかが一番の悩みどころでしょう。
以下で詳しく解説します。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
面積の求め方2通りをおさらいしましょう。
- 大きさが分かっている図形との相似比から求める方法
- 具体的に長さを求めて面積公式に当てはめる方法
本問は特に辺の長さは与えられていないので、2は使えそうにないですね。
加えて、「正六角形ABCDEFの面積を1とする」という表現から、面積比の問題である、という風にも解釈できます。
そこで、1の方法を使います。
正六角形ABCDEFにおいて、図のように対角線AD、BE、CFを引くと、これらは外接円の中心Oで交わり、6つの正三角形ができます。

正六角形の有名な性質で、中心角が6分割されることと外接円を使えば証明できるよ
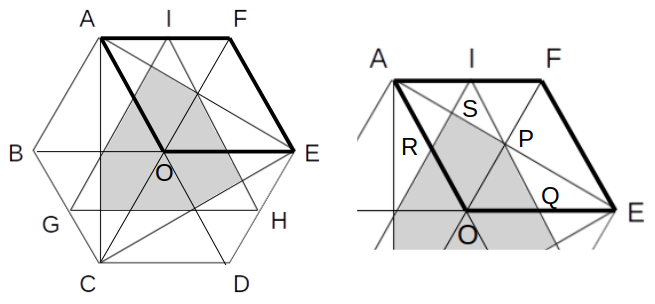
ここで、ひし形AFEOに注目すると、図形の対称性より、ひし形ABCOおよびCDEOは、灰色の部分を含めてAFEOをそれぞれ左右に120°回転させたものと一致します。
よって、灰色の領域全体の面積を求めるには、ひし形AFEO内の灰色の面積を3倍すればいいですね。
以下では、上の図(右)のように、交点をP、Q、R、Sとします。
△OPQと四角形OPSRに分けて順番に面積を求めましょう。
△OPQの面積
まず、△OPQに注目します。
△OEFの面積はすでに分かっている(6分割だから\(\frac{1}{6}\))ので、
△OPQ∽△OEFであることと、相似比が分かれば△OPQの面積が分かりますね。
これらのことを証明できないか、考えてみましょう。

PQ//FEっぽいね
実は、PQ//FEより△OPQ∽△OEFを示せます。
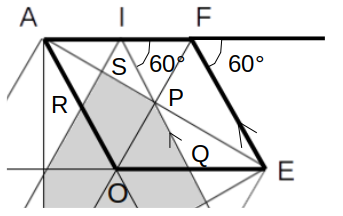
半直線AFを引くと、図のように正六角形の外角は60°です。
また、∠PIR=60°であり、対称性より∠PIF=∠AIRなので、∠PIF=\(\frac{180°-60°}{2}=60°\)
よって同位角が等しいので、PQ//FE
これにより、△OPQ∽△OEFが示されましたね。
あとは相似比ですが、これはもっと簡単です。
点Pはひし形の対角線の交点なので、OP=PFです。
これにより、△OPQ∽△OEFの相似比は1:2となります。

中学で習った懐かしの中点連結定理
面積比は1:4なので、△OPQ=\(\frac{1}{6}×\frac{1}{4}=\frac{1}{24}\)
これで、△OPQの面積が分かりました。
あとは四角形OPSRですね!
四角形OPSRの面積
四角形OPSRは、△OAPから△ARSを除いたもの、と考えるのがよさそうです。
△ARSの面積を求めるのには、やはり相似比を利用しましょう。
△ARS∽△AOPを示すのに、RS//OPではないかと当たりをつけます。
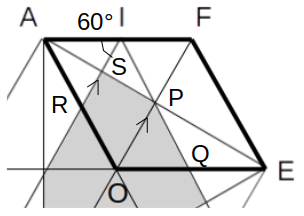
前項より、∠PIF=∠AIR=60°であることが分かってます。
さらに、△OAFは正三角形だったので、∠OFA=60°です。
よって、同位角が等しいことより、RS//OPが言えます。
ここで、点IはAFの中点なので、点RもAOの中点となります。
よって、△ARS∽△AOPの相似比は1:2です。
さらに、線分APは△OAFを二等分するので、△AOP=\(\frac{1}{6}×\frac{1}{2}=\frac{1}{12}\)
これより、△ARS=\(\frac{1}{12}×\frac{1}{4}=\frac{1}{48}\)
したがって、四角形OPSR=△AOP-△ARS=\(\frac{1}{16}\)
以上より、ひし形AFEO内の灰色の面積は、\(\frac{1}{24}+\frac{1}{16}=\frac{5}{48}\)
これより、灰色の部分全体の面積は、\(\frac{5}{48}×3=\frac{5}{16}\)
よって、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
面積の求め方は、公式か相似比かの2択です。
正六角形の内部にある、2つの正三角形の共通部分の面積を求める問題でした。
正六角形を6つの正三角形に分割したら、あとはひし形の内部にある領域の面積を2つのステップで求めます。
解説では厳密に証明しましたが、例えば「PQ//FE」とか「点RがAOの中点であること」などは、図を描いてそれっぽいな、と思ったら使ってしまってOKです。
正しければ選択肢のどれかにたどり着くはずなので、それを選んであとは他の問題に時間を使う方が賢明です。
数的処理は導出過程を見る試験ではないので、ある程度ざっくりしたやり方で素早く解答できる方が得点はアップします。
過去問レベルの演習をする段階になったら、得点に結びつけるための練習として、こうした抜け道を見つけることにも気を配ってほしいと思います。
国家総合職の教養試験はタイムマネジメントが明暗を分ける場合も大いにあるので、1問にかける時間が短くなれば、気持ち的にもかなり有利になります。
問題演習をするときは、自分なりのやり方で構わないので、より早く解答するテクニックを編み出してみてください!

楽をするための工夫は大事
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
正六角形ABCDEFにおいて、次図のように対角線AD、BE、CFを引くと、6つの正三角形に分割される。
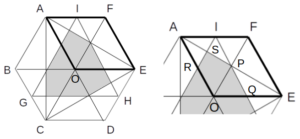
ひし形AFEO
ひし形AFEOに注目すると、対称性より、求める領域の面積はひし形AFEO内の灰色部分を3倍したものとして求めることができる。
さらに、この領域を△OPQと四角形OPSRに分割してそれぞれ面積を求める。
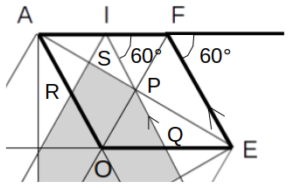
PQ//FEの証明
よって、△OPQ∽△OEF
また、Pはひし形の対角線の交点なので、相似比は1:2である。
これより、△OPQ:△OEF=1:4であるから
△OPQ=\(\frac{1}{6}×\frac{1}{4}=\frac{1}{24}\)
次に、次図の通り∠AIR=60°なので、RI//OF
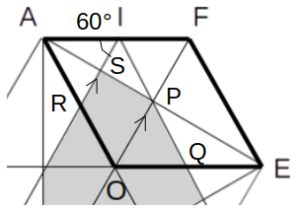
RS//OPの証明
よって、△OPQ∽△OEF
さらに、点IがAFの中点であることより、点RもAOの中点である。
よって、△ARS∽△AOPの相似比は1:2で、△ARS:△AOP=1:4
線分APは△OAFを二等分するので、△AOP=\(\frac{1}{6}×\frac{1}{2}=\frac{1}{12}\)
これより、△ARS=\(\frac{1}{12}×\frac{1}{4}=\frac{1}{48}\)
したがって、四角形OPSR=△AOP-△ARS=\(\frac{1}{16}\)
以上より、ひし形AFEO内の灰色の面積は、\(\frac{1}{24}+\frac{1}{16}=\frac{5}{48}\)
よって、灰色の部分全体の面積は、\(\frac{5}{48}×3=\frac{5}{16}\)
したがって、正解は4である。

コメント