こんにちは！
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【２】どこよりも詳しい解説
【３】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見！
ぜひ最後まで読んでいってください。
「解法のポイント」はないこともある、かもしれない
今回のテーマは……「展開図（空間図形）」
展開図って、形がいくつもあってややこしいですよね。
展開図のパターンを全部覚えるとかムリ！！！
とお困りのアナタに、とっておきの朗報。
展開図って、実は一つの形だけ覚えれば足りるんです。
なぜって、他のパターンは「面移動」で作り出せるから。
全パターンを覚える必要はない
例えば、立方体を思い出してみてください。
組み立てると、展開図の隣り合う辺は一体化しますよね。
このことを利用し、展開図の面を頂点まわりに回転させるのが面移動というテクニックです。
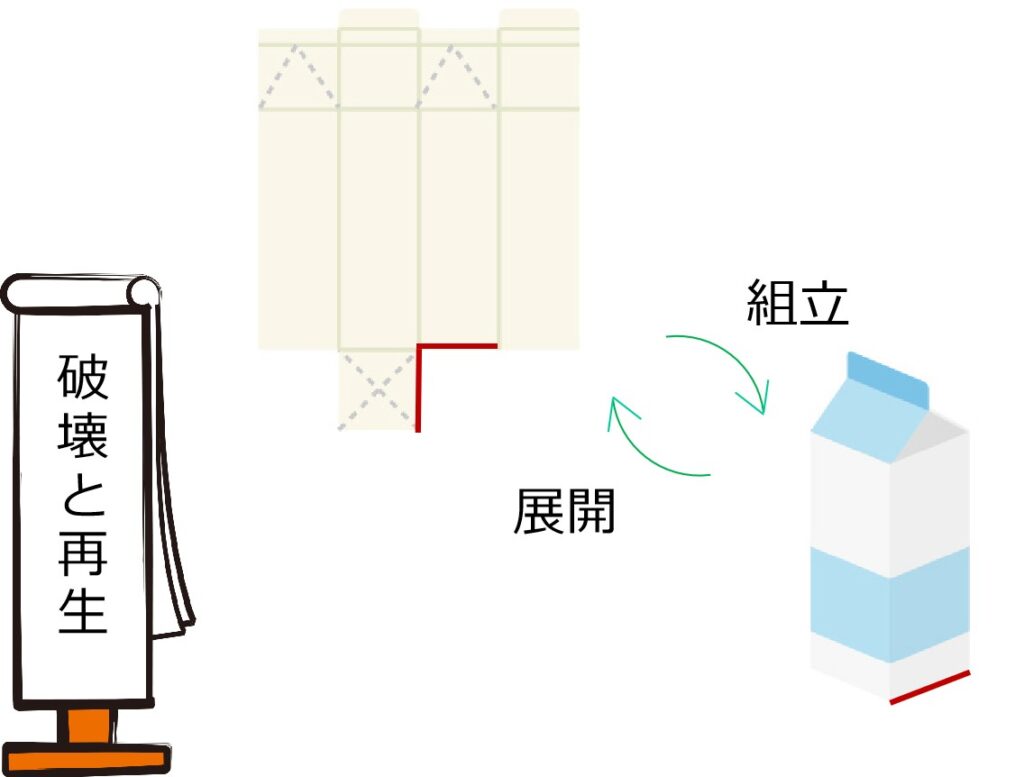
今回は、展開図の面移動を学べる問題を解説します。
いつものように、数的処理の過去問みたいな一問です。
演習問題：立方体の展開図とスクリーンに映る影
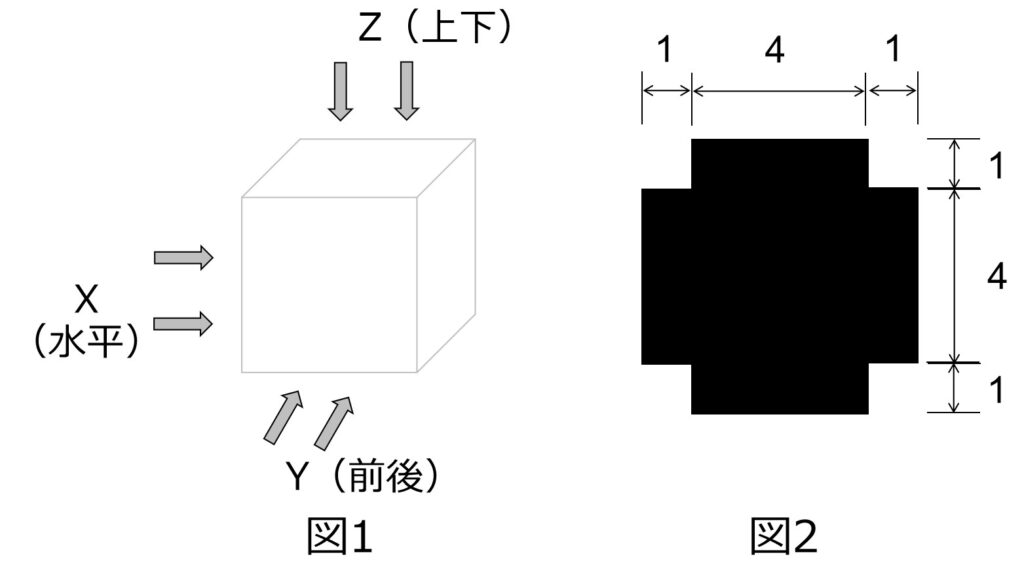
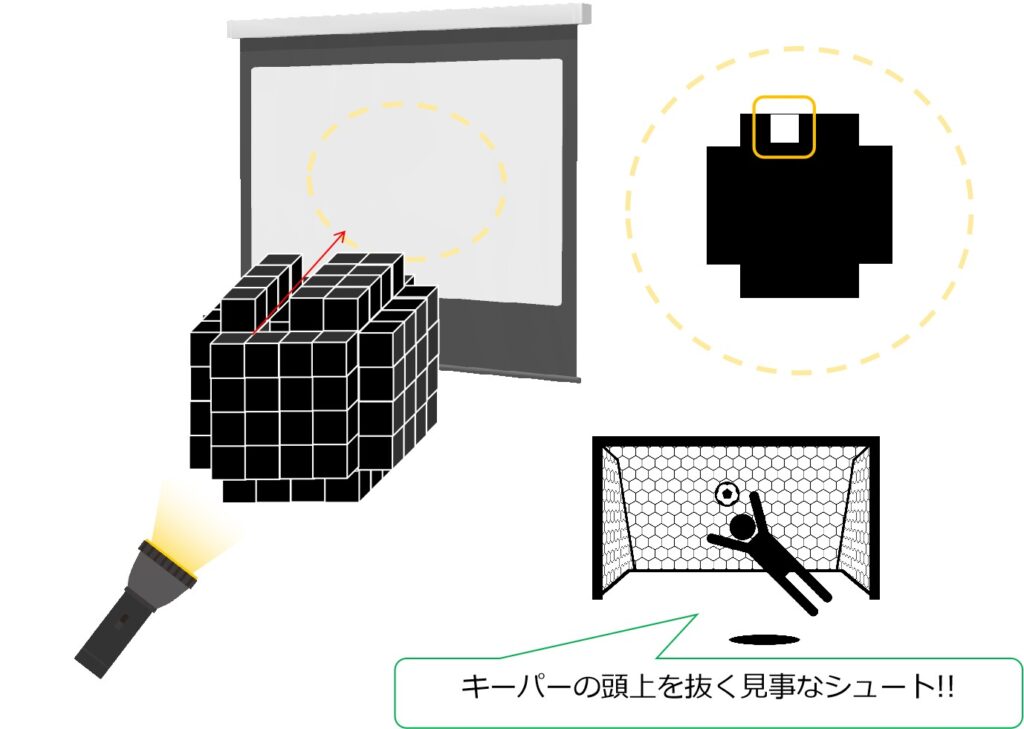
側面に1×1のマス目模様が描かれた、一辺の長さ4の透明な立方体Pがある。この立方体のマス目に、一辺の長さ1の黒色の立方体をいくつか貼り付けてできた立体をQとする。立体Qに、遠くから立方体の面に垂直な3方向（X,Y,Z）の光を当てたところ（図1）、対面のスクリーンに映る影はいずれも図2に示す形であった。図3より、立体QをPの辺に沿って切り開いた図として可能性のあるものを、図3から全て挙げたものとして正しいのは次のうちどれか。
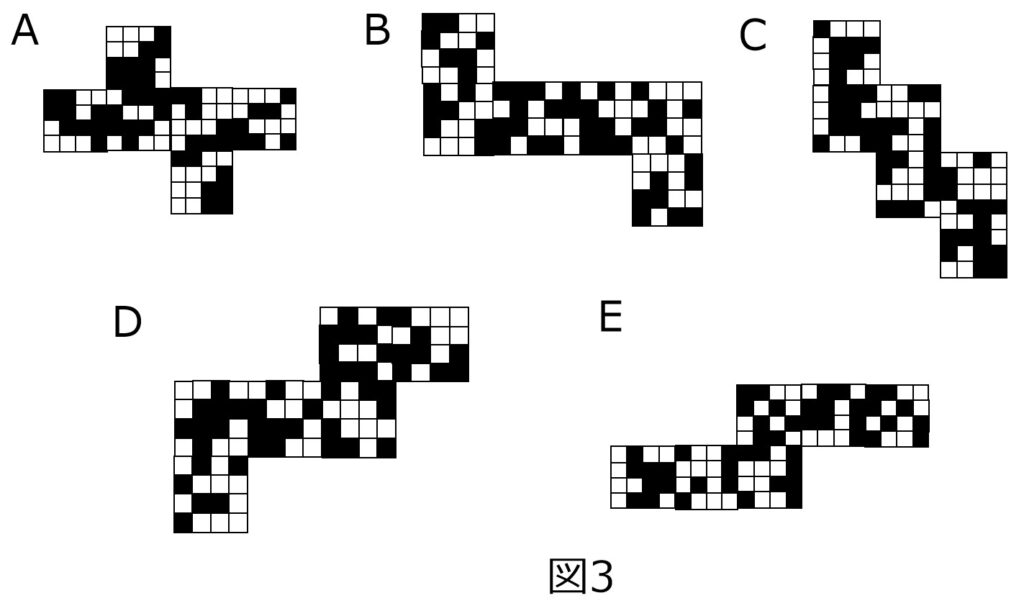
- AとC
- AとD
- CとD
- CとE
- AとDとE
２
影になるのはどんなとき？
↑これが分かれば、あとは展開図の問題。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者
おそすぎる自己紹介
それでは、解説スタート！
側面に1×1のマス目模様が描かれた、一辺の長さ4の透明な立方体Pがある。この立方体のマス目に、一辺の長さ1の黒色の立方体をいくつか貼り付けてできた立体をQとする。立体Qに、遠くから立方体の面に垂直な3方向（X,Y,Z）の光を当てたところ（図1）、対面のスクリーンに映る影はいずれも図2に示す形であった。図3より、立体QをPの辺に沿って切り開いた図として可能性のあるものを、図3から全て挙げたものとして正しいのは次のうちどれか。
- AとC
- AとD
- CとD
- CとE
- AとDとE
解説：展開図の面移動で立方体の対面を調べる
Q：スクリーンに影ができるには、何が必要でしょう？
→A：向かい合う面のいずれか一方にも黒ブロックがあること
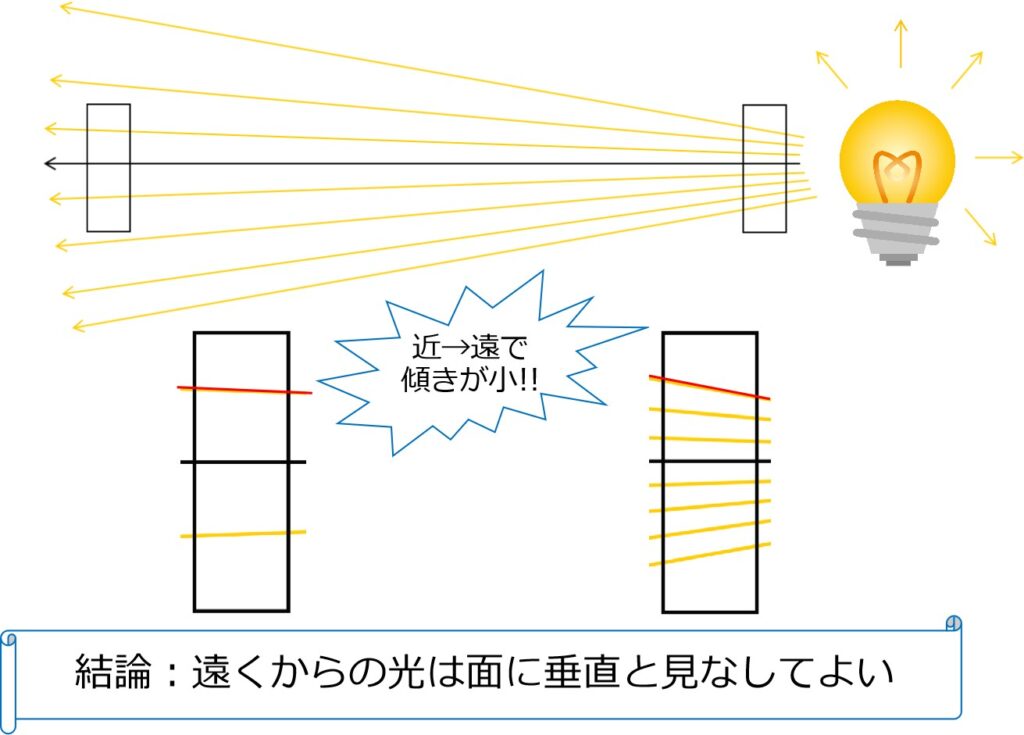
「遠くから」発せられた光は、立体Qの面に対しまっすぐ（＝垂直）に当たります。
まっすぐ進む光の進路上に「黒」があれば、その部分は影となります。
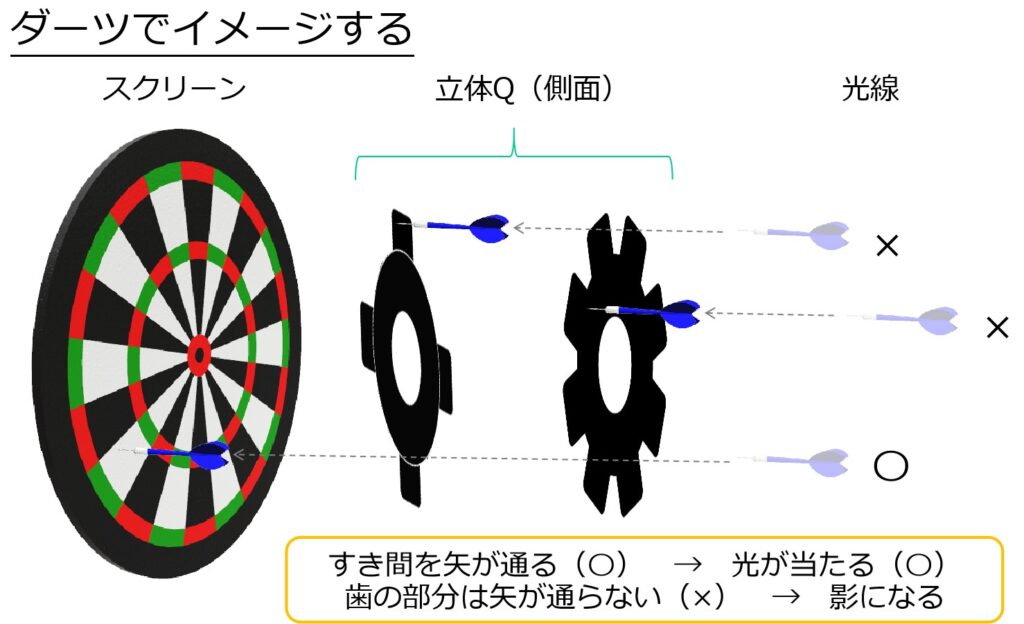
つまり、スクリーンに影ができるための条件は、
“向かい合う面のいずれか一方が黒であること”
この条件を踏まえて、AEの影の形を調べます。
遠くの光は平行？
本来なら、光源から出た光は、中心から遠ざかる向き（放射状）に広がります。
つまり、光の向きはバラバラのはず。
ですが！
光源が十分に離れた場所にある場合は、やって来る光線は互いに平行と見なすことができるんです。
理由：光源から遠ざかるほど光線1本1本の傾きが小
→傾き0（＝平行）でいーじゃん
展開図の面移動で向かい合う面が分かる
A～Eは、いずれも立方体の展開図。
展開図は、頂点を中心とした回転（面移動）による変形が可能です。
隣り合う辺は回転による面移動も有効
本問の目標は、向かい合う面の白黒を調べること。
向かい合う面のペアが分かりやすくなるように、展開図を面移動で変形させます。
（元の形のままで面のペアが分かるなら、もちろん変形はしなくてもOK）
もちろん、ちゃんと調べる方が確実だけど
今回は、立方体の展開図として一番ポピュラーな「十字架」を目指します。
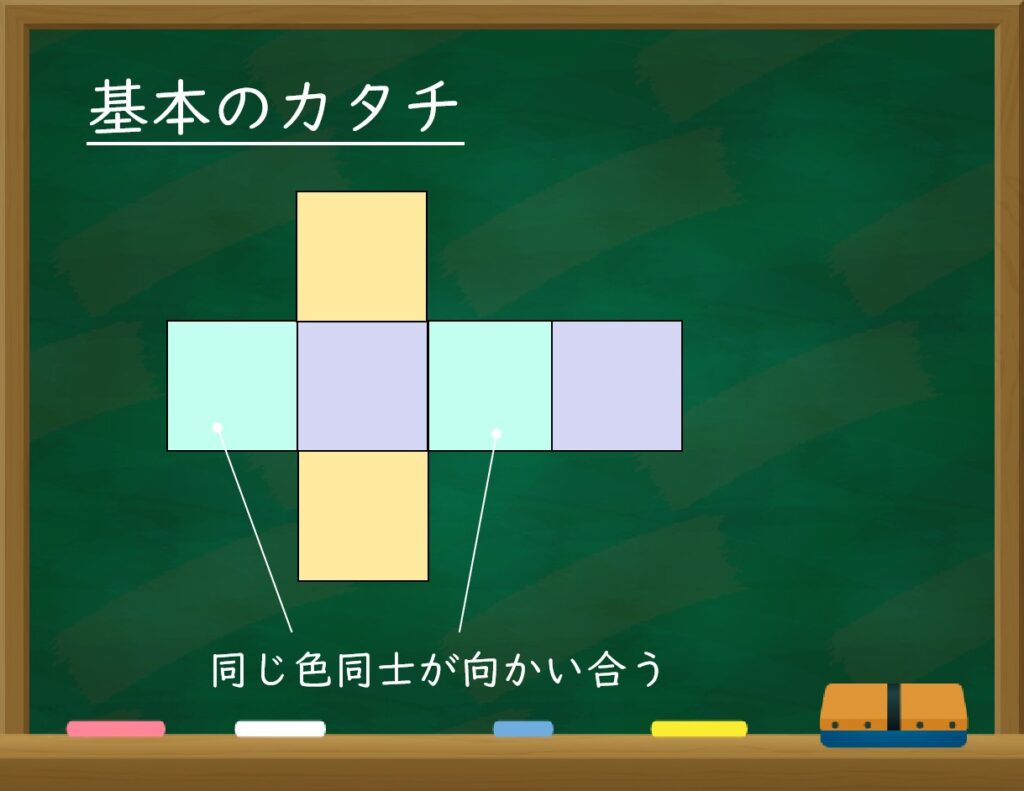
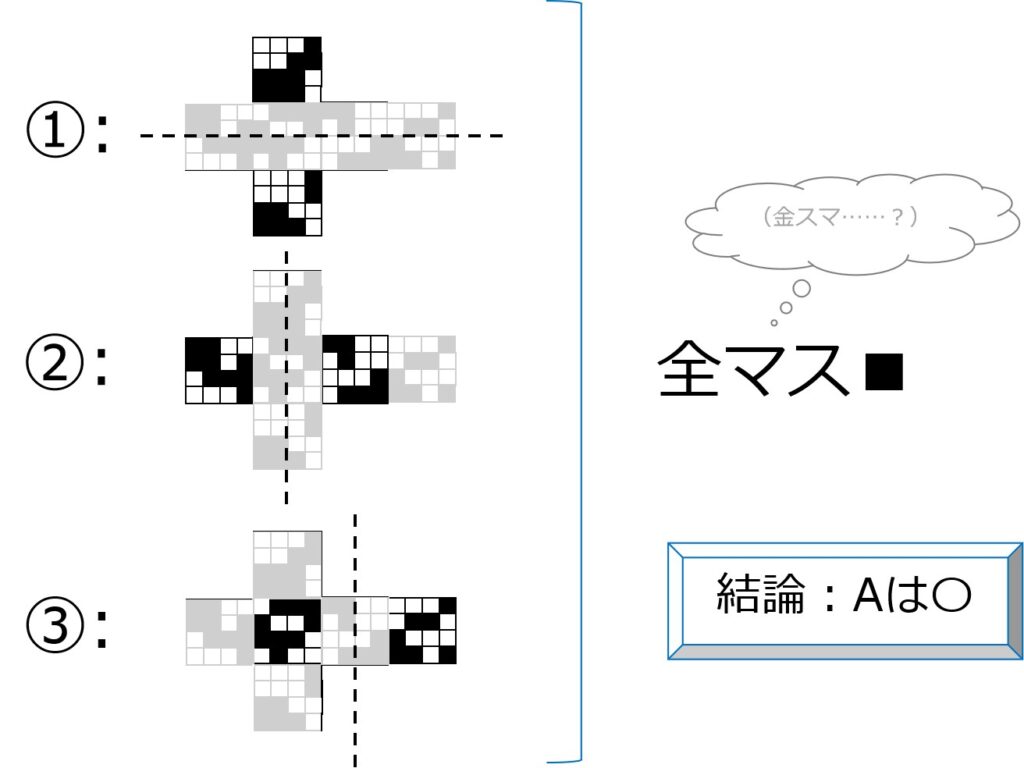
展開図A→◎：面移動で向かい合うマスを比較
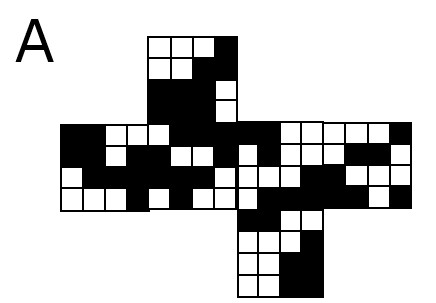
まずは面移動で「基本のカタチ」に変形したのち、向かい合う面を比較します。
Step1：「十字架」になるように面移動
一番下の段の正方形を左へ90°回転させれば「基本のカタチ」の形のできあがり。
カンタンですね
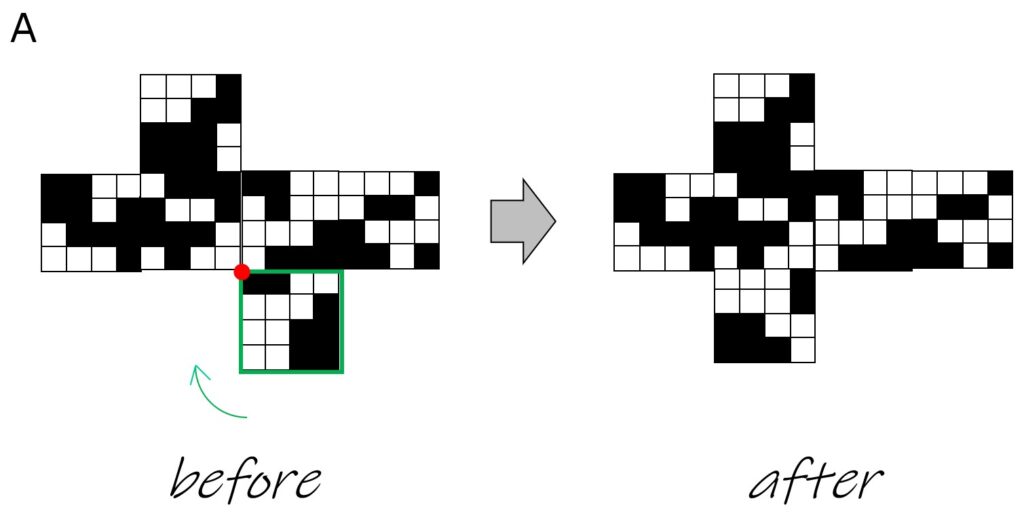
Step2：向かい合うマスの白黒を調べる
向かい合う面を見比べて、全てのマスが影となるかチェックします。
このとき、マスの対応にはご注意を。
影になる条件は、「展開図を組み立てたときに」向かい合う面の各マスが黒であること。
つまり、見比べるのは半分に折ったときに重なるマス同士でなければなりません。
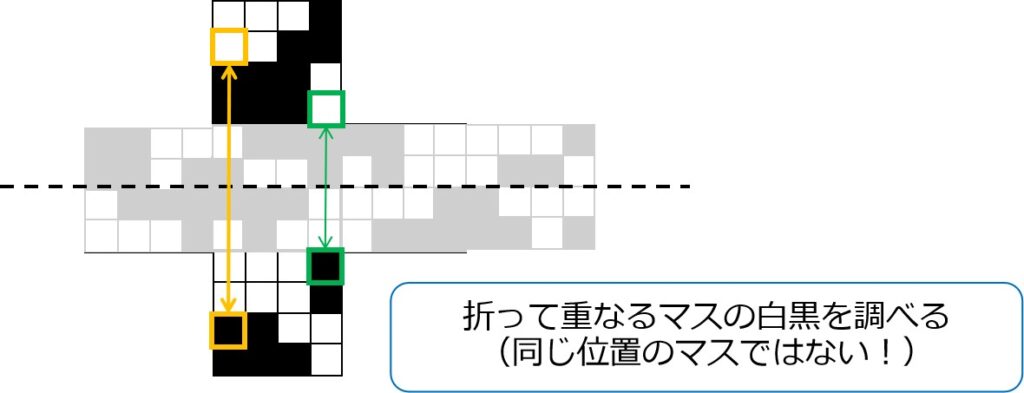
向かい合う面同士（線対称の位置）のマスを調べますと、全て影となることが分かります。
つまり、スクリーンに映る影は条件を満たします。
→Aは◎
1マスずつ、確実に見比べます
残りの展開図（B～F）も、同じようにチェックします。
展開図B→×：面移動を2回
はにわ形。
以下の面移動で、「基本のカタチ」になります。
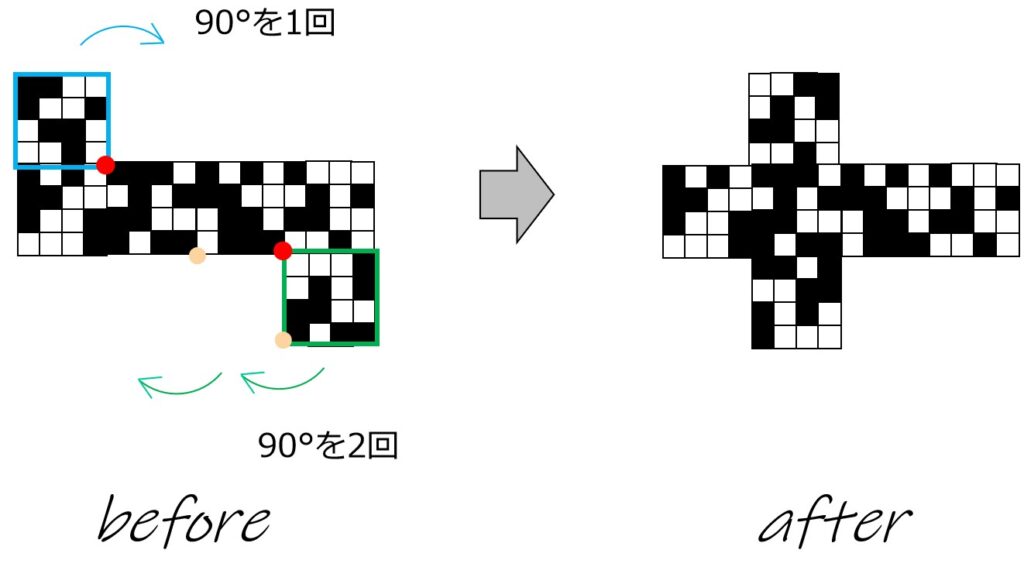
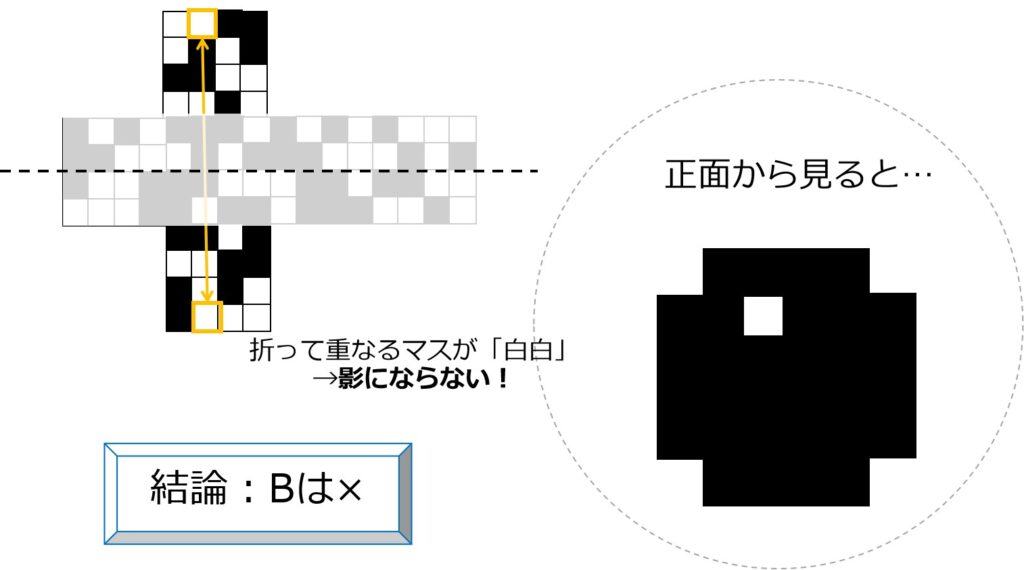
向かい合うマス同士を比較しますと……
上下の面において、影にならない箇所（赤枠）があります。
→Bは×
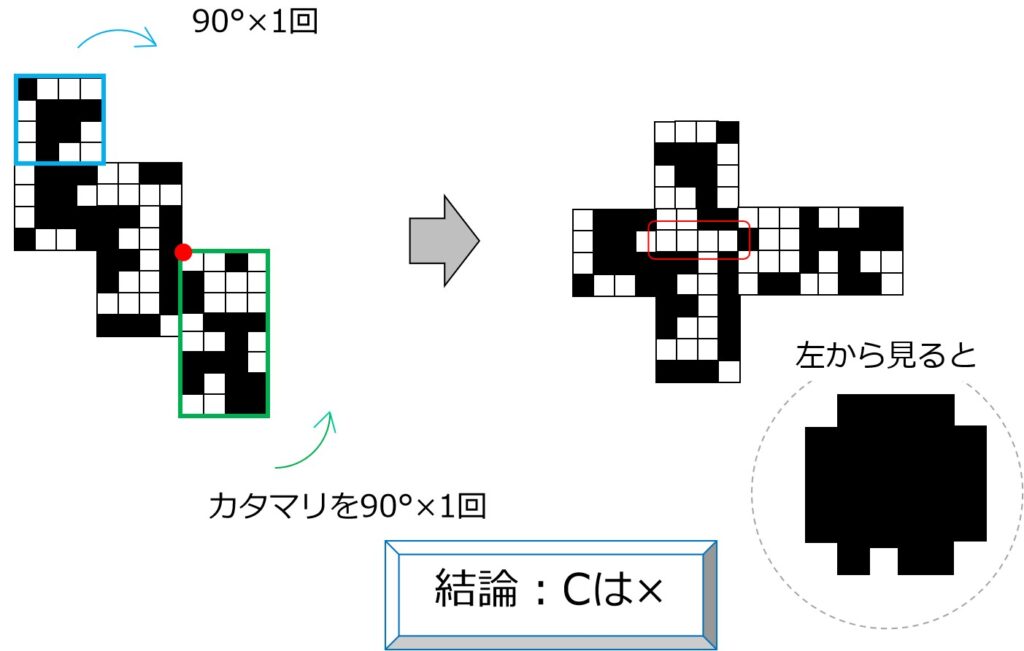
展開図C→×：カタマリの面移動
ネジネジ君と呼びましょう。
ここも、面移動で「基本のカタチ」に変形します。
向かい合うマスを見比べると、、、
図の赤枠は影になりません。
→Cは×
実をいうと、Cは面移動しなくとも候補から外せます。
与えられた影の形になるために、満たすべき条件がもう一つあるからです。
それは、縦横に白が4つ並ばないこと。
白が4つ並ぶ場所（上図赤枠）は光が通り抜けるので、影は「すきっ歯」のような形になります。
もとの展開図で「白4つ」に気づければ、Cは即除外できます。
キーパーがシュートほめてどうすんの
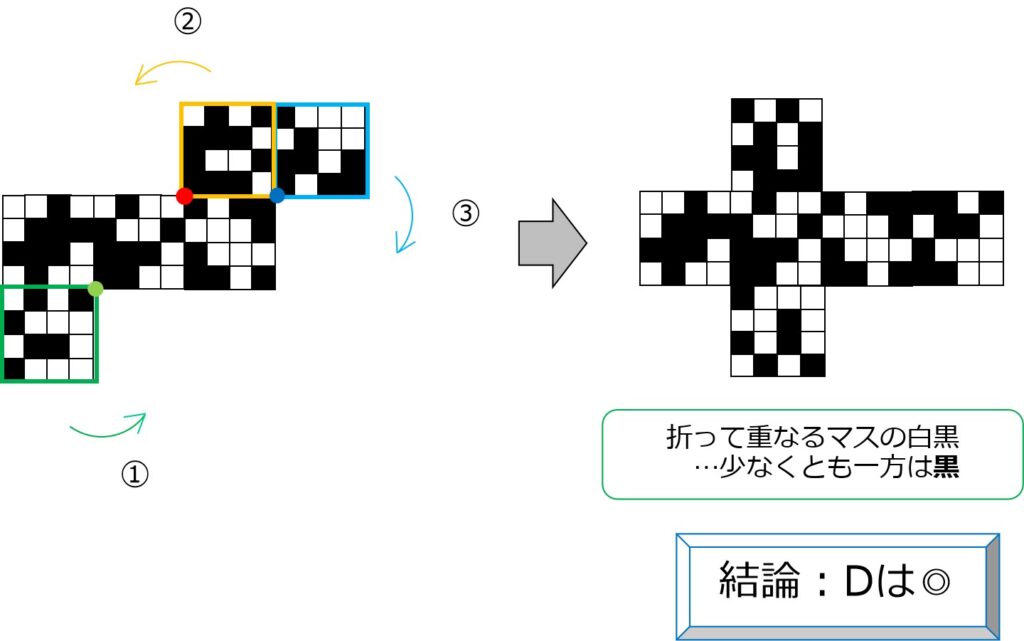
展開図D→◎：三々五々の面移動
お前マイクラにいたよな？
次の3ステップで、「基本のカタチ」に早変わり。
向かい合う面の、線対称なマスの白黒を調べます。
いずれも少なくとも一方に黒があり、かつ「白4つ」もありません。
→Dは◎
展開図E→×：面移動しても、しなくても
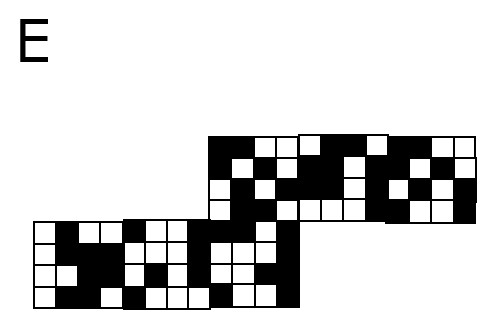
旧バイオ３に出てくる武器（マインスロアー）みたい。
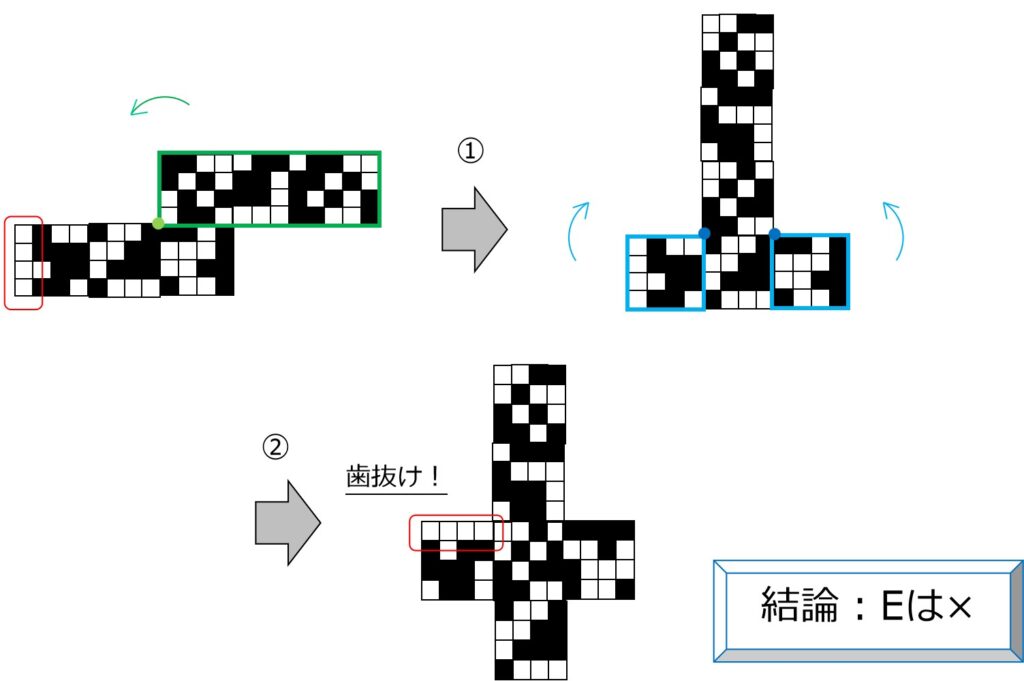
面移動：①カタマリ→②両脇の順に90°回転
白黒の条件はクリアしてますが、これはワナ。
図の赤枠は「白4つ」なので、影は歯抜けの形となります。
→Eは×
Cと同じく面移動なしに即断もできる
以上より、条件に合う展開図はAとD。
よって、２が正解です。
おわりに：立方体の展開図は「面移動」で作れる
お疲れ様でした！
立方体の展開図で厄介なのは、同じ立体でも形のパターンが複数ある、という点。
これは、切り開く辺の選び方の違いによるものです。
しかし、展開図の隣り合う辺は一体化する、という特徴を利用すれば、面の回転移動によって他のパターンをその場で作り出すことができます。
面移動があれば、展開図は覚える必要ナシ
過去にも展開図の問題を解説しています。
ゴールが見えると人は頑張れる。
全校集会は「以上をもちまして」からが本番なのよ
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！
この記事が参考になったら、ぜひシェアしてください！
Tweet次回もお楽しみに！
コメント