【国家一般職】同様に確からしいってなに？確率では同じものも区別しよう【玉の色が左右対称に並ぶ確率】

こんにちは！
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。

公務員試験を受ける方は必見！
ぜひ最後まで読んでいってください。

今回のテーマは……「同じものを含む確率（＆場合の数）」

「確率」といえば、数的処理では言わずと知れた頻出分野。
その中でも、今回は特に「同じものを含む確率」に焦点を当てて解説します。

ここ、つまずく方が非常に多いんです。
ありがちなのが、確率で同じものを区別する/しないの違いがよく分からない、という悩み。

ズバリお答えしましょう。

「区別したほうが確実」

です。
どういうことか？

今回は、確率の問題で同じものを区別する/しないの考え方を、ていねいに解説します。
後半では、過去問に似せた演習問題を解きながら、その使い方を学びます。

講義：確率で同じものは区別する？しない？

もう一度言います。
確率の問題では、同じものも

「区別したほうが確実」

です。

少し付け加えると、区別しないで数えられる問題もあります。
その場合、同じものの個数が一致している、という条件を満たしている必要があります。

それは、確率の定義には次のような「お約束」があるからです。

お約束：カウントする一つ一つのパターンの起こりやすさが同じであること

これが、「同様に確からしい」というやつです。
確率の場合、同じものを区別しないと、このお約束が崩れるケースがあります。

簡単な例を挙げて説明します。

例１：同じものを区別しないと間違えるパターン

まずはセオリー通り、同じものを区別して考えてみます。
白玉３つを、白A＆白B＆白Cと表します。

すると、玉の取り出し方は全部で４通り。
このうち、白玉であるケースは、A or B or Cのいずれを取るか、で３通り。

よって、確率は\(\frac{3}{4}\)→正解

では、同じものを区別しないとどうなるでしょう？

取り出し方は、黒か白か、の２通り。
白、という１通りが起こる確率は、\(\frac{1}{2}\)→×

この結果が間違いだ、というのは感覚的にも分かりますよね。
一体、なぜ間違えたのか？

間違いの原因は、同じものの個数が一致していないからです。
次の図を見てください。

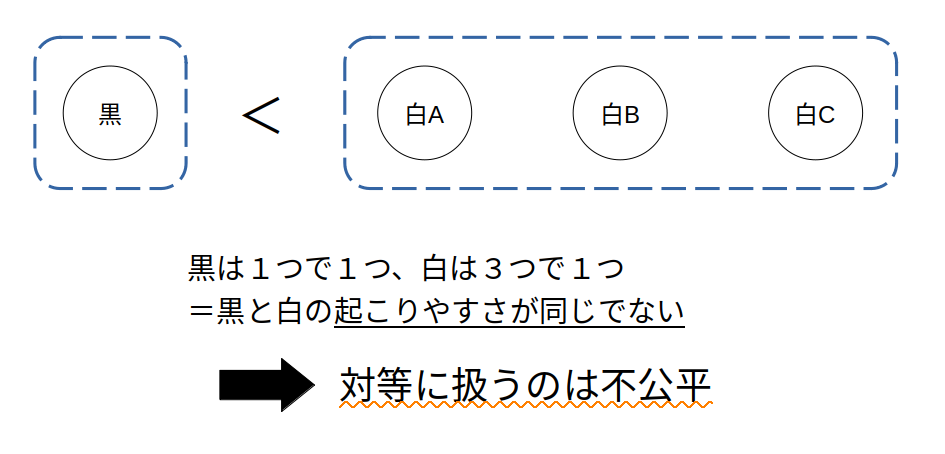
この場合、白３つをひと括りにして、黒１つと対等に扱っている点に問題があります。
だから、黒と白があたかも等確率であるかのように錯覚したわけです。

逆にいえば、黒と白が同じ個数なら、区別せず対等に扱えるということ。
次の例を見てください。

例２：区別しないでも解けるパターン

まずは区別する解き方から。
黒玉２つを黒A＆黒B、白玉２つを白A＆白Bと区別します。

玉の取り出し方は、全部で４通り。
このうち、白玉であるケースは、A or Bの２通り。
→確率\(\frac{2}{4}=\frac{1}{2}\)

本題はここから。
同じものを区別しないとどうでしょう。

玉の取り出し方は、区別しなければ、単に黒なのか白なのかだけ。
→全部で２通り
そして、白であるケースは１通り。

すると、確率は\(\frac{1}{2}\)

区別しないで数えても、正解を得ることができました。
これは、黒玉と白玉がともに２つだったからです。

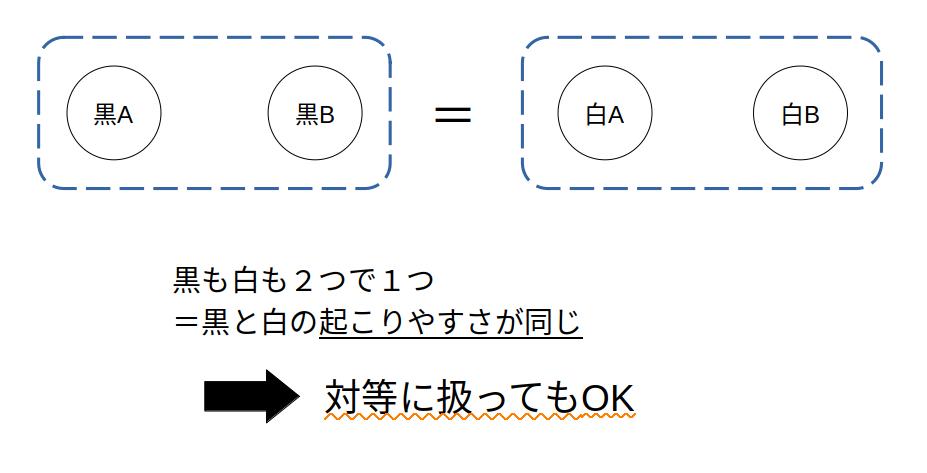
黒を取り出すことと、白を取り出すことの起こりやすさが同じであったため、対等に扱うことができたわけです。
これが「同様に確からしい」の考え方です。

結論：確率では同じものも区別すべし

このように、確率で同じものを区別しない解き方が使える場面はかなり限られます。
その点、同じものを区別する解き方は、幅広く使えるため実用性に優れています。

そんなわけで、確率の問題では同じものは「区別した方が確実」です。

以上、確率で同じものを区別する/しないの考え方の解説でした。

ここからは、過去問をもとに作ったオリジナルの演習問題を解きながら、「解法のポイント」の使い方を学んでいきます。

演習問題：玉の色が左右対称に並ぶ確率

袋から取り出した色の並びの問題。
左右対称となるのはどんな場合か、考えましょう。

以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。

おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

それでは、解説スタート！

問題文を見る

解説：追加の色で場合分けした確率を足す

確率の問題には、いくつかのアプローチがあります。
本サイトで以前紹介した、「解法のポイント」を思い出します。

まず、定義から求めるか、あるいは確率から確率を求めるか、ですが……
本問は前者のアプローチが良さそうです。

さらに、本問は【２】の解き方が有効ではないか、と予想できます。
「一列に並べる」と明言されてますし、８＋１個の並びを書き出すのは無理がありますからね。

追加した玉の色で場合分け

順列で数えるとすると、次に問題となるのは「追加した玉が何色なのか？」です。
色の内訳が決まらないことには、順列の計算ができません。

「色の並びが中央の玉の両側で左右対称となる」場合について、もう少し掘り下げてみます。

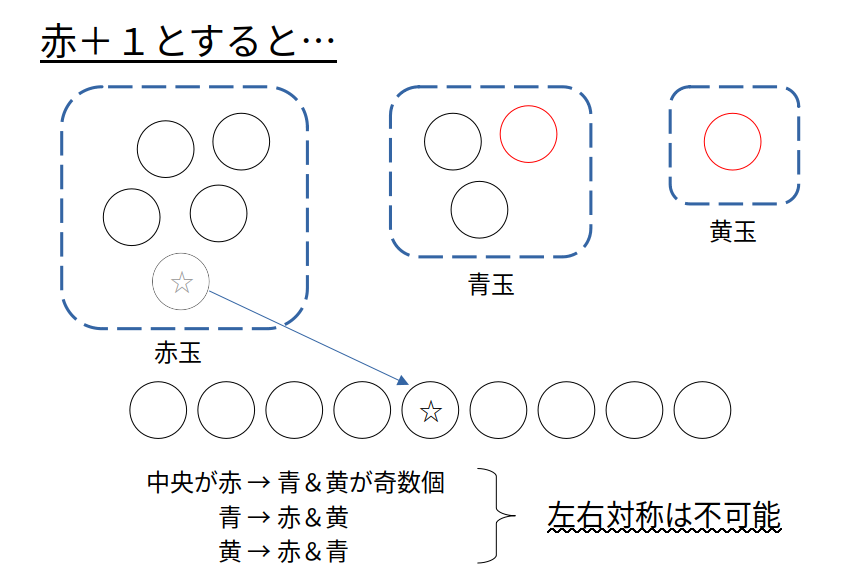
前提となるのは、両側の色の数が等しいこと。
つまり、中央の１つを除いた残りの数は、各色とも偶数でなければなりません。

このことから、始めに追加した色は青か黄のいずれかになります。
赤を追加した場合、中央を除いた８つの色の内訳に必ず奇数が含まれてしまうからです。

ここからは、追加した色が（i）青の場合と（ii）黄の場合に分けて、左右対称となる確率を考えます。

（i）青の場合：区別するなら選び方もカウントする

まず、９つの色の並び方は、全部で\(9!\)通り。

この場合の色の内訳は、赤４、青４、黄１です。
左右対称の条件を思い出すと、中央の１つは黄玉とするしかありません。

黄１を中央に固定したら、残った赤４と青４を左右均等に振り分けます。
左と右、それぞれに赤２と青２が並びます。

左右対称、ということは、左側の並びが決まれば右側も決まります。
つまり、左側の赤２＆青２の並びだけを考えればOKです。
ただし、同じ色の玉を区別するときは、４つのうちのどの２つを左側に持ってくるか、もカウントします。

赤（or 青）２つの選び方は、\({}_4 \mathrm{C}_2=6\)通り。
選び方一つ一つに対し、赤２＆青２の並べ方は\(4!\)通り。

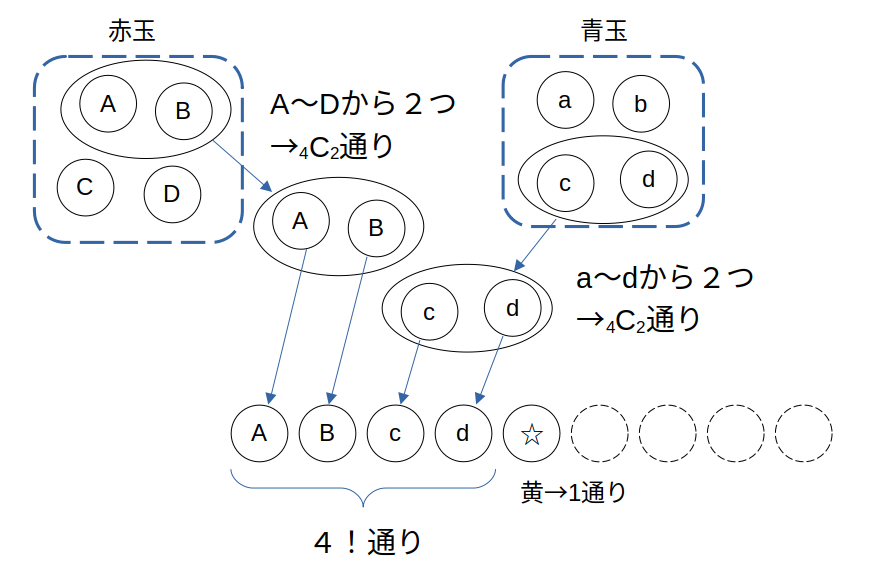
すなわち、左右対称の並び方は\(6×6×4!\)通り。

よって、（i）の場合の確率は\(\frac{6×6×4!}{9!}\)

（ii）黄の場合：中央の玉の選び方も忘れずに

９つの色の並び方は、全部で\(9!\)通り。

この場合の色の内訳は、赤４＆青３＆黄２です。
左右対称の条件より、中央の１つは青玉に決まります。

青３つを区別すると、どれが中央になるか、が３通り。

すると、左右それぞれに赤２＆青１＆黄１が割り振られます。
同じく、片側の並びが決まればもう片側も一つに決まるので、片側の順列だけ数えればOK。

赤２つの選び方は、\({}_4 \mathrm{C}_2=6\)通り。
かつ、青（or 黄）１つの選び方は、\({}_2 \mathrm{C}_1=2\)通り。
選び方一つ一つに対し、赤２＆青１＆黄１の並べ方は\(4!\)通り。

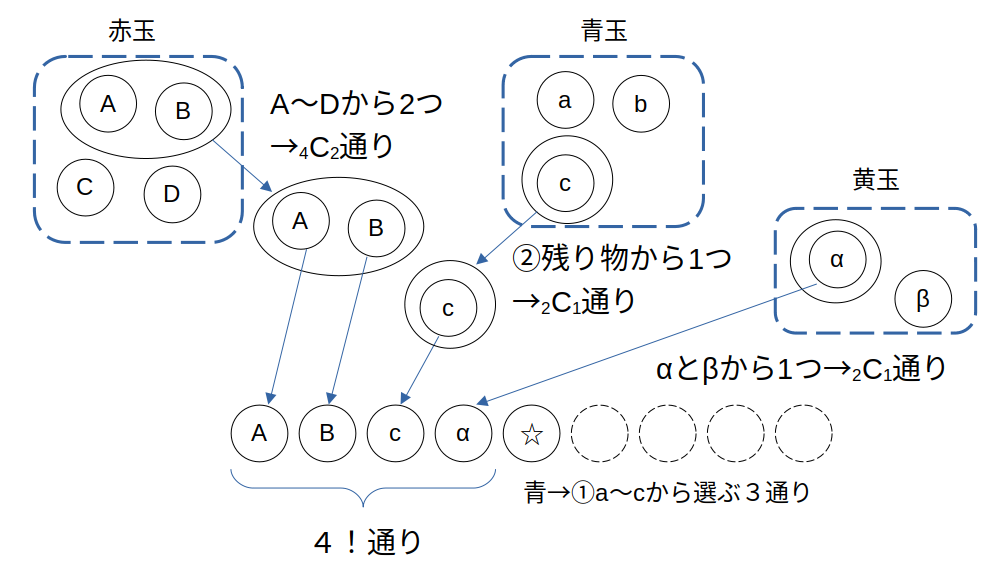
これより、左右対称の並び方は\(3×6×2×2×4!\)通り

よって、（ii）の場合の確率は\(\frac{3×6×2×2×4!}{9!}\)

以上、（i）と（ii）は同時に起こらない（＝互いに排反である）ので、足し合わせます。
左右対称に並ぶ確率は、

\[
\frac{6×6×4!+3×6×2×2×4!}{9!}=\frac{1}{140}
\]

よって、１が正解です。

おわりに：確率は「同じものも区別する」が基本

お疲れ様でした！

確率を考えるときは、同じものも「区別した方が確実」です。
区別しないで数えることのメリットは、計算がラクになること。
それも、区別する/しないの判断をする手間を考えれば些細なものです。
であれば、同じものも区別して数えた方がシンプルです。

今回は、９つの玉の色の並びが左右対称となる確率を求める問題でした。
左右対称となる条件より、追加の色は２つに絞れます。
追加の色で場合分けしたら、片側の並び方が何通りあるかを数えます。
「どれを片側に持ってくるか」の選び方をカウントするのを忘れずに。

確率の「解法のポイント」について、詳しく知りたい方は以下から。

最後までお読みいただきありがとうございました。

本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！

この記事が参考になったら、ぜひシェアしてください！

Tweet

次回もお楽しみに！

略解