こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
空からアクセス数降ってこないかなぁ。
前回は、子供会に参加した人の発言をもとにお菓子の個数を推測する問題をやりましたね。
問題を解くためのポイントはなんだったか、思い出せますか?
復習は完全に忘れてからするより、なんとなく覚えてる、くらいのタイミングでするのが最適です。
忘れてから見返すより短時間でできますし、思い出すだけなら空中でもできるのでおすすめです!
思い出す習慣を身につけて、効率的に学習を進めましょう。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
柔らかい素材でできた透明な立方体に対し、次の操作を順に行った。
- 頂点を3つ選ぶ。
- 選んだ3頂点を通る平面で切断する。
- 切断によりできた2つの立体のうち、体積の大きい方を残す。
- ウで残した立体において、切断により新たに生じた面のみを黒く塗りつぶす。
次に、できた立体に対し、再度ア〜エの操作を行った。その結果生じた立体に、正面および側面から垂直光を当てたところ、反対側に置いたスクリーンには次図に示す影が表れた。このとき、できた立体の頂点の数として正しいのはどれか。ただし、透明な面は光を透過し全く影を生じないものとする。
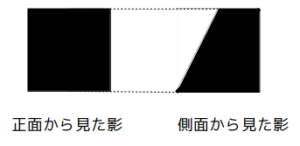
- 5個
- 6個
- 7個
- 8個
- 9個
2
立体図形の問題です。
正面から、あるいは真横から見るとどんな形をしているのか想像する空間把握力が必要です。
以下で詳しく解説します。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
まず1回目の切断について考えてみましょう。
立方体の頂点を3つ選んで切断する方法は、図形の対称性から、結局は次図の2通りしかありません。
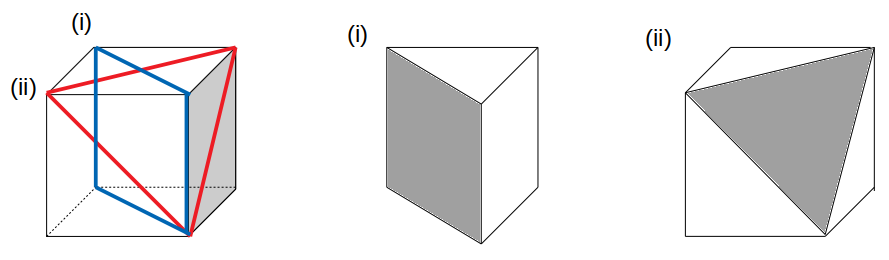
ここからは(i)と(ii)、それぞれ2回目の切断はどのようになるかを考えていきます。
(i)の場合
この場合、2回目の切断は次図に示すように、(i-a)と(i-b)の2パターンあります。
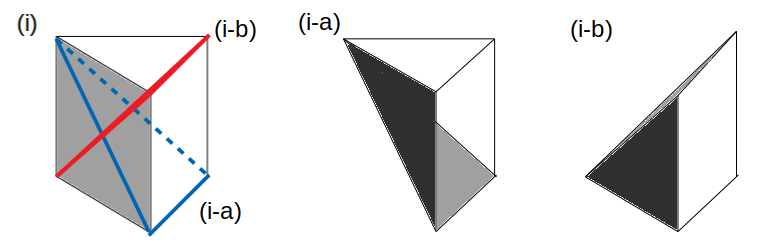
(i-a)と(i-b)、それぞれ正面と側面からの光によってできる影は次のようになります。
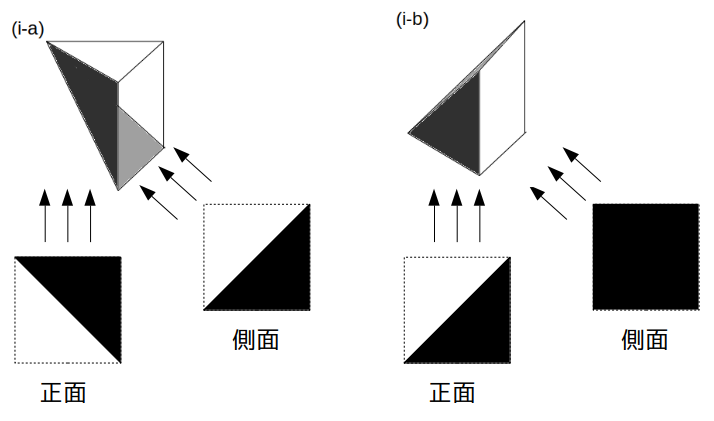
いずれも与えられた図とは異なっていますね。
そこで、今度は(ii)のケースを検討してみましょう。
(ii)の場合
この場合は2回目の切断のし方が何通りかあります。
全てを列挙するのも方法の一つですが、少々手間なので、ここは理屈で絞り込んでみたいと思います。
まず、1回目の切断でできた立体について、正面および側面から見た様子を考えると次図(左)のようになります。
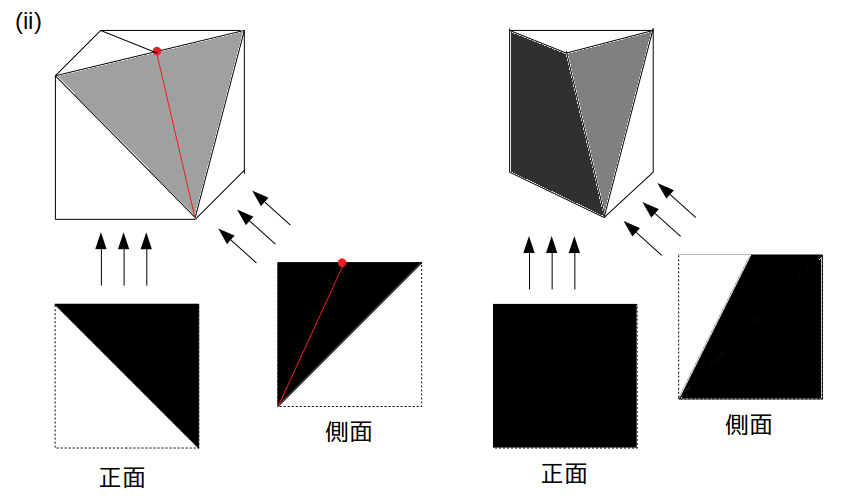
側面の図を問題と見比べると、赤線より左側の部分が欠けてなくなっていますね。
これは2回目の切断による変化なので、赤線は2回目の切断の切り口を側面から見た様子であることが分かります。
図の赤い点は中点であることに注意しつつ、切り口の赤線をもとの立体図に書き込むと上図(左)のようになります。
2回目の切断は、赤線で示される線を含み、かつ灰色の面に対し垂直な平面に沿って行われると考えれば、切断により生じる立体は上図(右)のようになります。
これを正面から見ると、問題で与えられた図と同じ黒塗りの正方形となるので、これが問題の立体であったと分かります。
頂点の数を数えると6個なので、2が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
立体の切断にともなう見え方の変化を追う問題でした。
前半は立体の形が比較的単純なのもあり、全パターンを網羅する解き方で進めています。
対して後半は、現状(1回目の切断)と終着点を見比べて、論理的考察により求める立体の形を明らかにしています。
このように、状況に応じて違った解き方を使う臨機応変さも時には必要です。
通常、書き出すなら書き出すやり方に固執しがちなところですが、解き進めてその先の分岐があまりにも多すぎる場合などは、切り替えて論理的に答えを導けないかどうか考えてみるのも一つの手段になります。
そうした思考法は数的処理全般に通用するものですが、本問ではそれ以前に立体図をイメージして描く力が必要でしたね。
特に、イメージできても正しい図が描けないと、考察を進めるのは困難でしょう。
(私は絵を描くのが苦手で、せっかくイメージしても図として表現できないので詰まってしまう、ということも多々ありました汗)
対策としては、解答の図をマネて描いてみる、というやり方もあります。
国家総合職の数的処理で出題されるのは、ほとんどが正多面体(特に正四面体と立方体)なので、最低でもそれらの図は展開図も含めて描けるように練習しておくとよいでしょう。
私は正八面体が描けなかったので何度も練習してました。
空間図形に苦手意識のある方は、正多面体をマネて描く練習から始めてみてはどうでしょう?
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
次回もお楽しみに!
略解
まず1回目の切断について、図形の対称性から、切り方は次の2通りに限られる。

1回目の切断
2回目の切断は、次図に示すように、(i-a)と(i-b)の2パターンが考えられる。
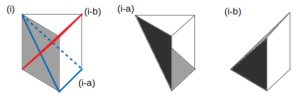
2回目の切断(i)
正面および側面から当てた光による影の見え方は、それぞれ次図の通りである。
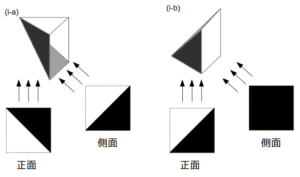
(i-a)と(i-b)の見え方
いずれも問題で与えられた見え方と一致しないので、(i)は不適。
(ii)の場合
まず、1回目の切断でできた図の影の見え方は次図(左)のようになる。
これに対し、1回目の切断の側面図における赤線の左側が欠損するような切断を考えると、赤線を含み灰色の面に垂直な平面による切断が適切であると分かり、できた立体は次図(右)のようになる。
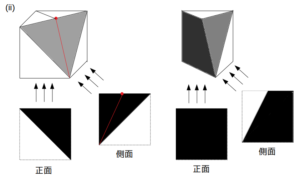
2回目の切断(ii)と見え方
この図に示すように、正面および側面から当てた光による影は問題に与えられたものと一致する。
この立体の頂点の数を数えると、6個である。
したがって、正解は2である。

コメント
はじめまして。
いつも楽しく勉強させて頂いています。
解説の(ii)の、側面から見た影ですが、
この影は1回目の切断面のみを投影されたものではないでしょうか?
2回目の切断面は台形ですが、側面からの投影でも台形になると思います。
つまり、側面から見た影の、右下半分の直角三角形部分も、
黒く塗りつぶされる範囲になるのではないでしょうか。
または、黒く塗りつぶした面に後ろから光を当てた場合、
光を透過し全く影を生じない、という条件が必要ではないでしょうか。
コメントありがとうございます。
ご指摘の通り、(ii)で切断後の側面の影は台形となります。
対応して問題の図を修正し、辻褄が合うようにいたしました。
解答のプロセスに大きな変更はありません。
いつも見ていただきありがとうございます!
最近は投稿のペースが落ちてますが、がんばって更新してますので引き続きご活用いただけると嬉しいです。
また何かあれば遠慮なくコメントください。