こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
前回は、会議の座席レイアウトを決める問題でした。
典型的な位置関係の問題です。
ある程度勉強されている方はもちろん、参考書を終えたばかりの方にも、力試しにうってつけの内容になっています。
解いてきた方は、お疲れ様でした。
せっかく苦労して問題を解いたんですから、本番で活用できるように復習をやりましょう。
何回か手を動かして解き直してみると、新たな発見が得られるのでおすすめです。
インプットonlyでは、得られる学びにも限界があります。
きちんとアウトプットすることで、記憶に定着しやすいだけでなく、解法の使い方もマスターできます。
解いたことある問題を確実に習得して、足元を固めましょう!
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
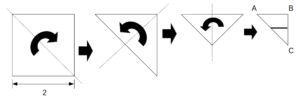
図のように、1辺の長さが2の正方形の紙を3回折ってできる三角形ABCにおいて、2つの辺AC、BCの中点を結んだ太線を切り取り線として切断した。切断後の紙を展開して得られる図形のうち、面積が最小のものを直線上に置いて滑ることなく1回転させたとき、その図形が通過する領域の面積はいくらか。
ただし、通過する領域に重複する部分がある場合は、これらを別個の図形と見なしたときの面積を求めることとする。例えば、通過する領域が図のような共通部分を持つ二つの円であった場合、求める面積は\(S\)と\(T\)の和である。
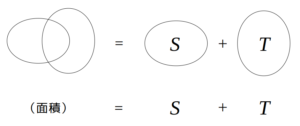
- \(2\pi +1\)
- \(2(\pi +2)\)
- \(3\pi +2\)
- \(3(\pi +2)\)
- \(4\pi +1\)
2
折り紙と通過領域の複合問題です。
回転させる図形がどんなものかをつかむのが第一歩です。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
折り紙のように図形を折りたたむ問題では、どんな 規則多くは線対称 に従って折りたたんだのかに注意しながら、各ステップを逆にたどって展開しましょう。
線対称の軸に注意
本問では、3回とも真っ二つ(=線対称)に折っているので、どこが対称軸か、ということに注意しつつ、次図のように1ステップずつ順に展開していきましょう。
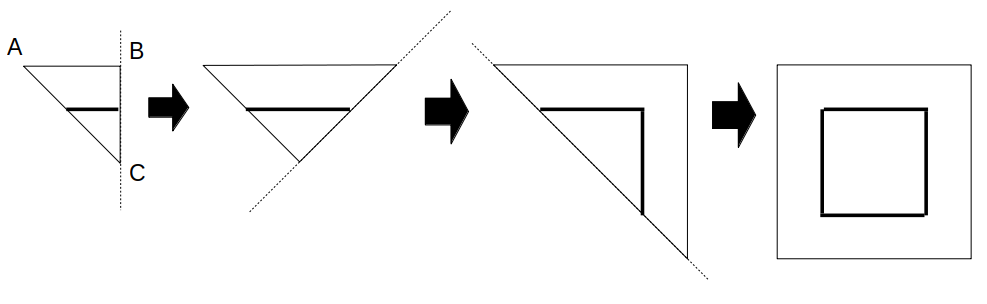
展開した結果を見ると、面積が最小の図形は太線の正方形です。
これを直線上で転がすわけですが、先にこの正方形のサイズ(=辺の長さ)を求めておきましょう。
太線の正方形の1辺の長さを\(x\)とおきます。
すると、△ABCにおける切り取り線(太線)の長さは\(\frac{1}{2}x\)と表せます。
一方、紙の正方形の1辺は2なので、線分ABの長さは1です。
△ABCに中点連結定理を用いると、\(\frac{1}{2}x×2=x=1\)
よって、太線は1辺の長さが1の正方形であったと分かります。
あとは、これを直線上で転がせばOKです。
国家総合職といえば、「対応関係」
なんとほぼ毎年(!)、出題されています
対策はバッチリですか?
不安なあなたに、おすすめの一問があります↓
\\\【7つの部屋の割り当て】///
この問題、条件を整理するだけで8割方解けてしまうんです。
対応関係では必須の、条件を整理して可視化するスキルを磨いてみませんか?
Twitterもよろしくね!↓
試しに\(\frac{1}{4}\)回転させてみると、通過領域は次図のようになります。
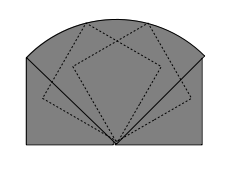
この図からも分かるように、\(\frac{1}{4}\)回転させたときの通過領域は、扇形と直角三角形2つに分割できます。
まず扇形については、半径は\(\sqrt{2}\)、中心角は90°なので、面積は
\(\pi(\sqrt{2})^2×\frac{1}{4}=\frac{\pi}{2}\)
また、2つの直角三角形は、底辺および高さがともに1なので、面積は
\(1^2×\frac{1}{2}×2=1\)
合計すると、\(\frac{\pi}{2}+1\)となります。
回転によって得られる通過領域は、この図形の繰り返しによって表現されます。
1回転させた場合は、次図(上)のように重複する部分が生じますが、これを\(S\)と\(T\)のように分することで、次図(下)を得ます。
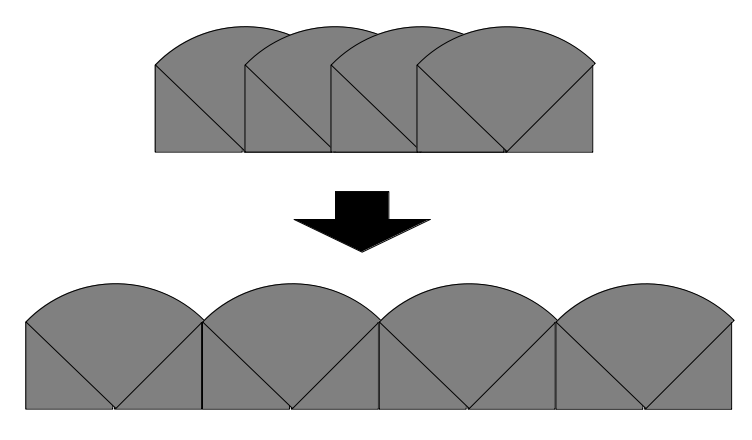
これより、求める面積は、\((\frac{\pi}{2}+1)×4=2(\pi +2)\)
よって、2が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
回転する正方形の通過領域を考える問題でした。
図形を折りたたむ問題では、対称軸に注意しつつ1ステップずつ展開しましょう。
本番では展開する過程も含めて手書きしないといけませんが、焦らず丁寧に向き合いましょう。
思考の過程を記録として残しておけば、後で見直しにも役立ちますから、無駄にはなりません。
最小の図形が何であるかさえ突き止めれば、あとは1回転させるだけです。
通過領域をイメージするときは、回転の中心と、その中心から最も遠い点が描く軌跡を追いましょう。
折り紙の問題はそれほど多くありませんが、1回転したときの軌跡を考える問題は時折見かけるテーマです。
参考書でも数的処理の一分野として掲載があると思いますので、中級レベルまでの問題は対策しておきましょう。
脳内で回転をイメージする力は、空間把握力にも通じる部分があるので、空間図形の対策も兼ねて練習してみてください。
最後に、本サイトで過去に扱った軌跡の問題を載せるので、ぜひチャレンジしてみてください!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
切り取り線も含めて折りたたんだ図形を展開すると次のようになる。
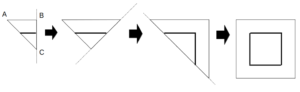
折り紙の展開
太線の正方形の1辺の長さを\(x\)とおくと、△ABCにおける切り取り線(太線)の長さは\(\frac{1}{2}x\)
また、紙の正方形の1辺は2であるから、線分ABの長さは1
△ABCに中点連結定理を用いると、\(\frac{1}{2}x×2=x=1\)
よって、太線は1辺の長さが1の正方形である。
これを直線上で\(\frac{1}{4}\)回転させると、通過領域は次のようである。

回転による通過領域
扇形について、半径は\(\sqrt{2}\)、中心角は90°なので、面積は
\(\pi(\sqrt{2})^2×\frac{1}{4}=\frac{\pi}{2}\)
また、2つの直角三角形は、底辺および高さがともに1なので、面積は
\(1^2×\frac{1}{2}×2=1\)
合計すると、\(\frac{\pi}{2}+1\)
題意の通過領域は、次図のように、\(\frac{1}{4}\)回転した図形を4つ並べたものなので、面積は
\((\frac{\pi}{2}+1)×4=2(\pi +2)\)
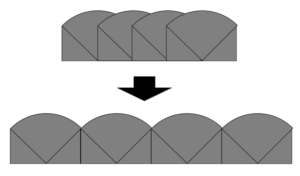
1回転の通過領域
したがって、2が正解である。

コメント