こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
ギリギリで年内最後の更新になるかもしれない今回。
年が明けたら、直前期で本サイトの需要が高まることを期待して。
- 展開図に必須のテクニック「面移動」が身につく
- 過去問の類題を例に、本番で役立つ「解法のポイント」の使い方を学べる
- どこよりも詳しい演習問題の解説で、本試験レベルの問題を完全理解
→数的処理の「あと一点」が実現!
数的処理の対策で、「空間図形」をおろそかにしてはいけません。
なぜなら……
- 例年1〜2問、1問はほぼ固定で出題がある
- 捨て問にする人が多いため、差が付きやすい
そんな空間図形で多いのが、「展開図」にまつわる問題です。
組み立てたり切り開いたり、という操作を頭の中で正確にできればいいですが、なかなか難しいものです。

筆者は絵心ないから苦労してた(←絵心関係ある?)
しかし、苦手なあなたももう大丈夫。
展開図は平面のまま考えることができます。
この記事では、公務員試験の数的処理で出題される展開図の問題を解くためのコツである「解法のポイント」を紹介します。
それから過去問の類題を一緒に解いて理解してもらうことで、本番で使える解法を身につけていってもらいます!
講義:展開図は面移動で解く
展開図の問題を攻略するカギは、「展開図を自在に変形させること」です。
隣り合う辺は回転による面移動も有効
展開図は、切り開く辺の選び方によっていくつか形のパターンが存在します。
例えば立方体なら、次のような11通りの展開図が考えられます。


11種類も覚えられないって
もちろん全て暗記するのが一番手っ取り早いですが、その必要はありません。
どれか一つだけ覚えてればOKです。
一つ知ってれば、残りは「面移動」で導き出せるので。
上で出た立方体の展開図であれば、次のような面の「回転」によって別のパターンを順次作り出すことができます。
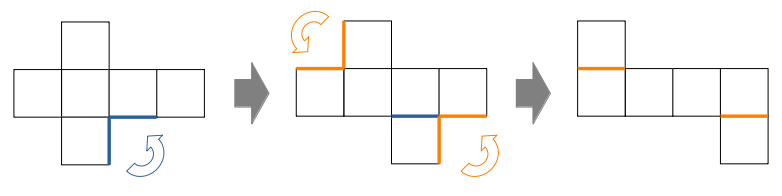
この「面移動」において、各面の隣り合う辺に注目です。
展開図で隣り合う2辺は、立体を組み立てたときに重なるので、任意にくっつけたり切り離したりできます。
つまり、展開図は面の「回転移動」によって変形させることが可能です。
これは立方体に限った話ではなく、相手が正四面体だろうが、正二十面体だろうが同じです。
展開図に関する問題は、面の移動による変形を求められるケースがほとんどです。
でも、回転移動が可能であることを知ってれば、もとの立体を想像せずとも機械的に別の展開図を描けます。
(問)
(答)
立方体の展開図の問題 | 中学受験準備のための学習ドリル
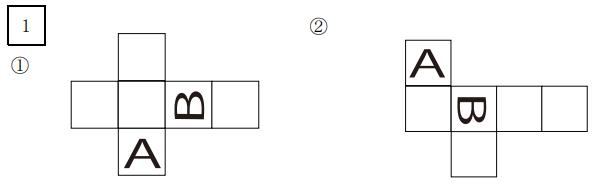
この例題では、組み立てたときに「A」の右隣に来る面はどれか、が分かればOKです。
次のように、「A」の右隣に空白の面が来るように面移動を行うと、「B」の位置と向きが分かります。
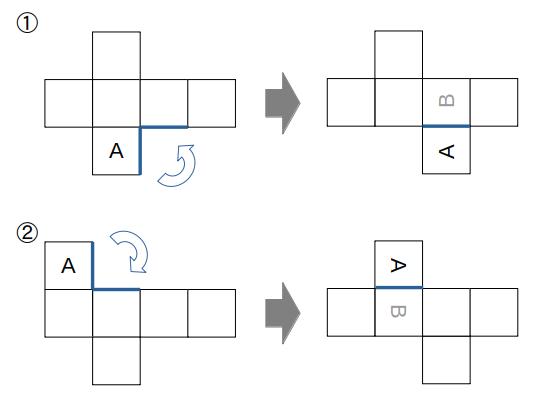
演習問題:模様付き立方体の展開図
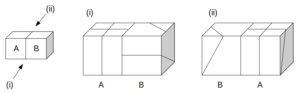
図のように、模様の付いた2つの立方体が、一つの面で接した状態で置かれている。この立体を(i)および(ii)の方向から見た様子は同図の通りである。ただし、接した面に描かれた模様は2つの立方体で一致しており、底面には模様がない。このとき、AおよびBの展開図の組み合わせとして正しいのは次のうちどれか。
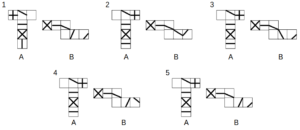
2
立方体の展開図の問題です。
空間把握能力と展開図の基本的な扱い方を知っているか、が問われています。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説
正解の展開図を描く
まずすべきことは、AとBの正解にあたる展開図を描いてみることです。
表裏から見た様子が与えられているので、これらをヒントにAとBの展開図を作成します。

ここは多少の空間把握力が必要
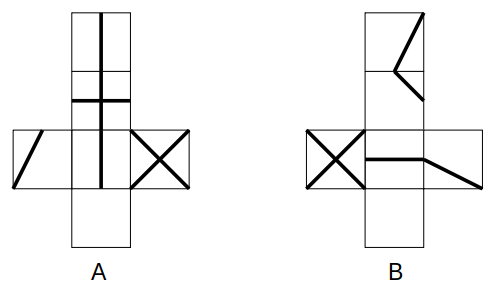
なお、与えられた選択肢より、接触した面の模様は×印であると分かります。
この展開図が選択肢のどれに一致するのかを調べます。
ただし、この形のままでは比べられないので、展開図を別の形に書き換える必要があります。
ここで、講義の「解法のポイント」を思い出してください。
組み立てたときに一致する辺(=隣り合う辺同士)であれば、くっつけたり切り離したりできるんでしたね。
隣り合う辺は回転による面移動も有効
このテクニックを利用して、選択肢の形になるように正解の展開図を変形させます。
Aの展開図:基準となる模様の並びを決めて面移動
次図のように、Aの展開図を時計回りに90°回転させ、赤枠に示す模様の並びに注目です。
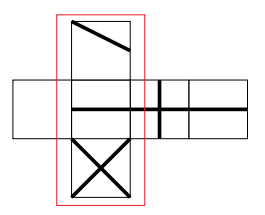
選択肢をよく見ると、5択のいずれにもこの赤枠の模様の並びが表れてます。
このことを利用し、以降は赤枠の並びを基準に考えましょう。
つまり、赤枠の並びはそのままに、残り3面を移動させることで、選択肢にあるT字型の展開図に書き換えるのです。
前述の通り、もとの立方体を組み上げたときに一致する辺に注目し、面を移動します。
まず、中心にある4面の並びを作りましょう。
上図で一番右の面(=横一直線の模様)を移動させます。
基準となる「赤枠の並び」を崩さないように、×印の下に移しましょう。
次図に示す赤線の二辺が一致するので、ここにくっつけます。
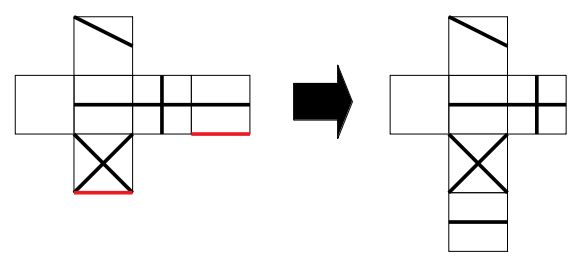
次に両脇の2面(十字と白の面)ですが、選択肢を見ると多少の違いはあれど、どれも一番上の斜め線の横に付いているので、ここに移動させましょう。
この場合はもっと簡単で、隣り合う2辺が一致する辺になります。(赤線同士と青線同士)
移動させると次図のような展開図ができます。

90度回転で色を付けた辺を一致させる
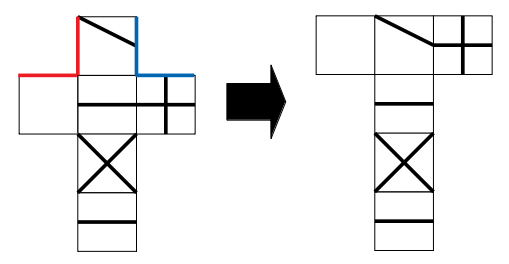
これでAの展開図は完成です。
選択肢と見比べると、1が候補から外れますね。
同じように、Bの展開図も調べましょう。
Bの展開図:一致する辺の見極めが重要
Bについては、次図に示す赤枠の模様の並びに注目します。
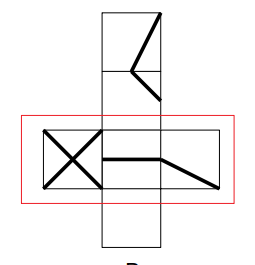
選択肢を見ると、いずれにもこの3つの模様の並びが含まれていることが分かります。
このことより、以下ではAのときと同様、赤枠で示す3面の並びを基準に展開図を書き換えます。
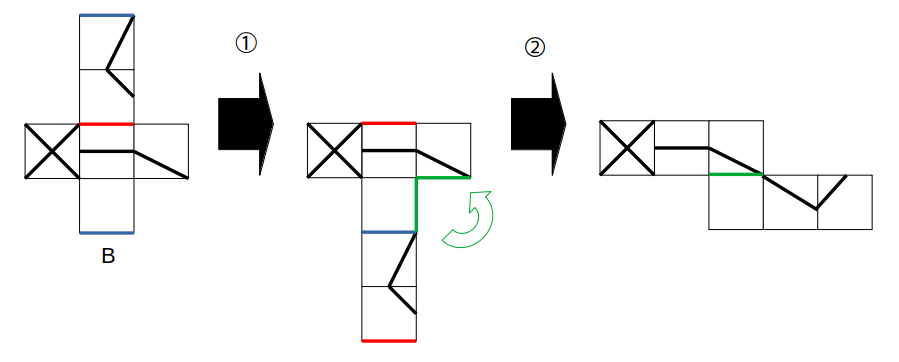
まず、選択肢の展開図に則り、一番下にある白い面を右へ一つ隣に移動します。
次図に示す赤線が一致するので、次のように面を移動させることができます。
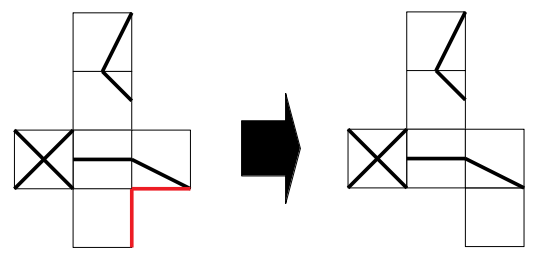
次に、一番上の斜め線の面を移動させます。
組み立てた立方体をイメージすると、次図における赤線が一致する辺なので、次のように白い面の右隣にくっつけます。
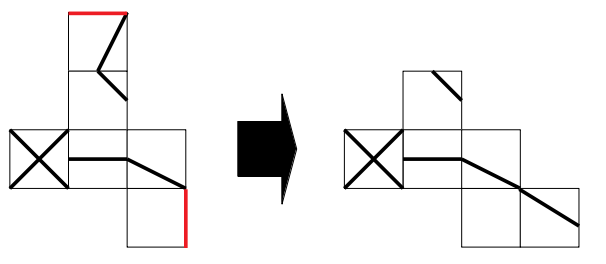
あとは一番上の短い斜線模様の面ですが、組み立てると次図の赤線が一致するので、次のように移動させることができます。
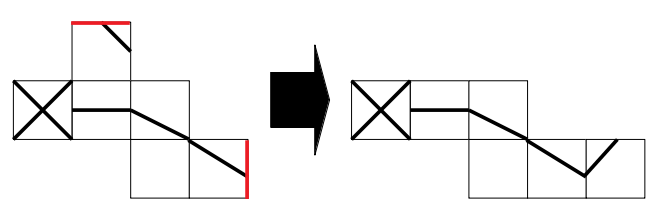
これで、Bの展開図も完成です。
選択肢を見ると、作成したBの展開図と一致するのは2しかありません。
よって、2が正解です。
おわりに:展開図のコツは面移動
お疲れ様でした!
いかがだったでしょうか?
展開図は一致する辺を見つけて面移動させるのが基本です。
2つの視点を表した図から展開図を作成する問題でした。
頭の中で組み立てのしやすい展開図(本問では十字型にしてます)を書いたら、もとの立体を想像しながら面移動し、選択肢に与えられた展開図の形に変形しましょう。
選択肢をよくよく見ると、Aの展開図は「1」と「それ以外」の2通りしかないのに対し、Bは1〜5の全てが異なっています。
このことからBの展開図だけ調べれば解答できる、という点に気づければ、手順がかなり少なくなります。
いつも抜け道が見つかるとは限りませんが、日頃から解答時間を短縮する方法はないか、検討してみるのは良いことです。
数的処理は時間勝負なので、自分がやりやすく、少しでも短時間で解答できる方法があれば積極的に取り入れるべきです。
国家総合職では、毎年1〜2問は空間図形分野からの出題があります。
頭の中で展開図を組み立てたり、立体を回転させたりする能力(=空間把握力)を養いましょう。
「空間把握力はセンス」と言われがちですが、努力でカバーできる部分もあります。
正四面体や立方体、正八面体くらいまでは脳内で展開したり回したりできるようになっておきたいものです。
あとは、立体や展開図を手書きできるようにするのも意外に重要です。
本番では自分で図を描いて考える必要がありますからね。

筆者は正四面体とか四角すいとか、手書きできるように練習してたよ
最後までお読みいただきありがとうございました!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
AとB展開図はそれぞれ次のようになる。
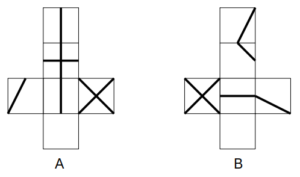
AとBの展開図
これをもとに、選択肢に与えられた形の展開図を作成する。
まずAについて、上図の展開図を時計回りに90°回転させる。
すると、次図の赤線で示す2辺は組み立てたときに一致するから、次のように面を移動させることが可能である。
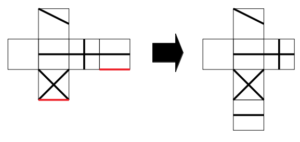
4面の並びを作る
さらに、次図の赤線と青線も一致するから、次のように両端の2面を移動させることが可能である。
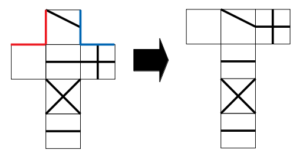
T字型の展開図を作る
次にBについて考える。
最初の展開図において、次図に示す赤線が一致することから、次のように白い面を移動できる。
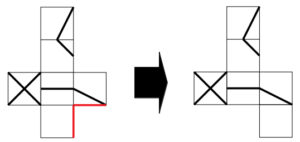
白い面を右へ一つ隣に移動
さらに、次図に赤線で示す2辺も一致することから、次のように面を移動する。
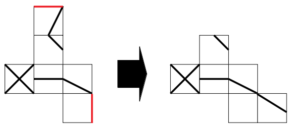
一番上の面を白い面の右隣に移動
また、次図の赤線も一致するから、次のように面を移動する。
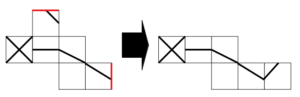
一番上の面を右端に移動
以上、出来上がったAとBの展開図をもとに選択肢を検討すると、正しいのは2しかない。
よって、正解は4である。



コメント