こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
カフェインを摂りすぎると疲れやすくなるんだそうです。
私は飲むとやる気がアップするので、特に記事を書くときはついつい手が伸びてしまいます。
こういうのって結局は元気を前借りしているようなものなので、飲みすぎるとあとでどっと疲れが押し寄せてくるんですよね。
何事もほどほどが肝心なようです。
前回は、日直と週番の担当者を決める問題をやりましたね。
国家総合職ではおなじみ、対応関係の問題なので、解いてない方はぜひ挑戦してみてください。
もう解いた方は、今一度、解法の手順を思い出してみましょう。
自分がつまずいた箇所とか、新しく知った解き方などは特に重要です。
思い出せない方は、復習のサイクルを早めてみてください。
完全に忘れてしまう前に思い出すのが復習のコツですよ。
数的処理に限らず、新しく問題を解いたら、ちょっとしたスキマ時間に解き方を思い出すようにすると、短時間で知識が定着しやすくなるのでおすすめです。
復習がバッチリな方は、本日の問題へ参りましょう!
本日の演習問題
ある旅行会社の社員15人が、1人ずつ5つの観光地A〜Eを訪れ、それぞれに1〜5点の異なる点数を付けて評価した。社員1人が評価を決定するたび、観光地ごとに合計点を算出し、合計点による順位付けを行った。合計点と順位について、次のことが分かっているとき、確実にいえるのはどれか。
- 13人目の社員までの評価の合計点について、Aが40点、Bが38点、Cが35点であり、同率の(合計点が一致した)観光地はなかった。またこのとき、1位と2位の合計点の点差は2点以上で、1位と5位の合計点の点差は10点未満であった。
- 14人目までの社員の評価を集計すると、同率の観光地がCを含めて3つあった。
- 14人目の社員と15人目の社員は、DとEに対しそれぞれ同じ点数を付けた。
- 15人目までの社員の評価を集計し、最終得点を求めたところ、同率の観光地が2つあった。
- Aの最終得点は45点であった。
- Bの最終得点は41点であった。
- Eの最終得点は40点であった。
- 最終得点が同率の観光地の一方はAであった。
- 15人目の社員によるCの評価は2点であった。
4
観光地の5段階評価を集計して、合計得点と順位の変動を追跡する問題です。
13人目までの合計点を考えることから始めましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
解説
13人目までの各観光地の合計点から考えましょう。
A〜Eに1〜5の点数を与えるので、持ち点は1人あたり15点です。
すると、13人目まででは15×13=195なので、195点をA〜Eに割り振ることになります。
13人目までの合計点は、Aは40点、Bは38点、Cは35点なので、DとEの合計点を合わせたものは195-(40+38+35)=82点です。
これを単純に二等分すると41点ですが、条件「同率の(合計点が一致した)観光地はなかった」より、これはあり得ません。
ここから、合計が82となる2つの整数の組み合わせは、片方から1取ってもう一方に加える、を繰り返すことで以下のように得られます。
| 41 | 42 | 43 | 44 | 45 |
| 41 | 40 | 39 | 38 | 37 |
| × | × |
条件「1位と5位の合計点の点差は10点未満」を考慮すると、Cが35点なので、(45, 37)以降の組み合わせは考えなくてよいですね。
よって、DとEの合計点の組み合わせは
(42, 40)、(43, 39)、(44, 38)
のいずれかとなります。
さらに、「Aが40点、Bが38点、Cが35点」であることと、「同率の(合計点が一致した)観光地はなかった」を考慮すると、(42, 40)と(44, 38)が消え、DとEの合計点の組み合わせは(43, 39)に決まります。
ただし、DとEのどちらが43点(または39点)であったのか、というのはまだ確定しません。
| 41 | 42 | 43 | 44 | 45 |
| 41 | 40 | 39 | 38 | 37 |
| × | × | ○ | × | × |
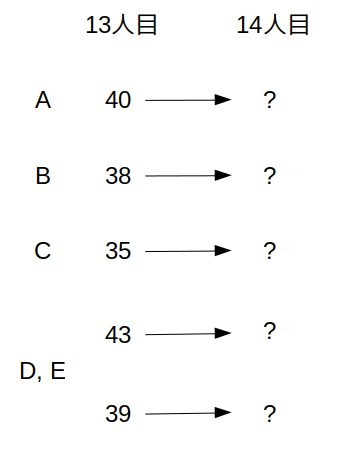
次に、条件「14人目までの社員の評価を集計すると、同率の観光地がCを含めて3つあった」について考えます。
Cは13人目の時点では35点なので、14人目の評価を加えた合計点は36〜40点の間になります。
このうち、36点 or 37点 or 38点 or 39点では、3人が同率となるのは不可能です。
よって、Cを含む3人が同率で40点の場合を考えることになります。
同率となる3人は、CとBと39点の観光地(D or E)になります。
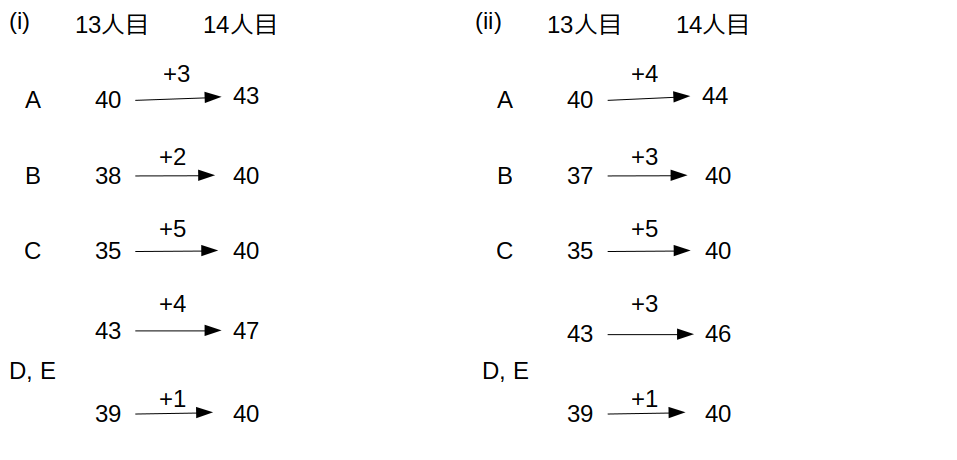
14人目によってAに与えられる得点が、(i)3点のときと(ii)4点のときで分かれます。
これら2パターンについて、条件「14人目の社員と15人目の社員は、DとEに対しそれぞれ同じ点数を付けた」を適用してみます。
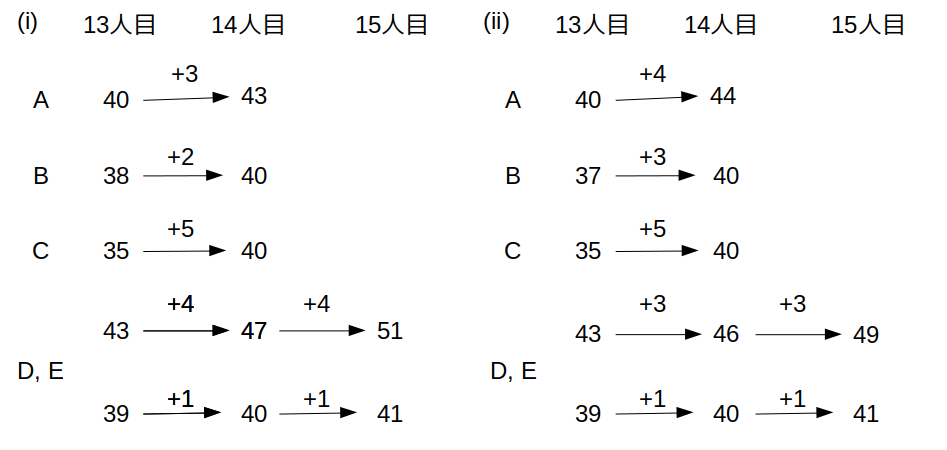
ここで、条件「15人目までの社員の評価を集計し、最終得点を求めたところ、同率の観光地が2つあった」を考えてみます。

「同率の観光地」ってどこよ?
A〜Cに、「+2」 or 「+3」 or 「+5」のいずれかを使って同じ数字を作れるでしょうか?
結論。
「A+2=(B or C)+5=45」
とすることができます。
(i-a)B+5の場合と、(i-b)C+5の場合の2パターンが条件を満たします。
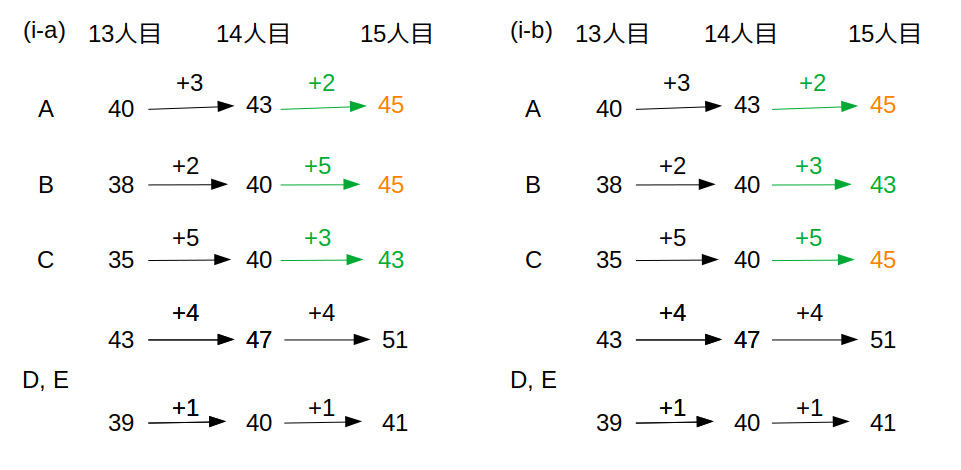
次に、(ii)の場合。
この場合に条件を満たすのは、、次の2パターン。
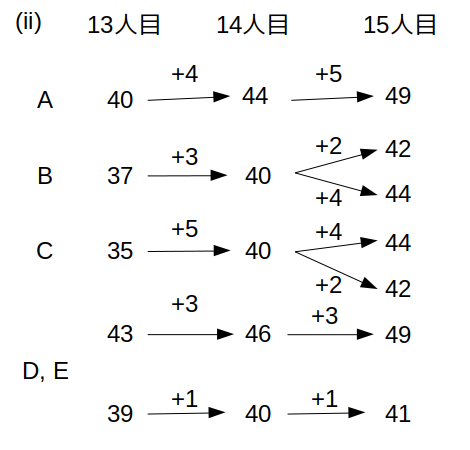
与えられた条件で確定するのはここまで。
(BCとDE、それぞれの対応は確定しない)
以上より、4が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
観光地の評価を推測する問題でした
しかし、フタを空けてみれば、途中経路を含み最終的な合計点が確定したのはAだけでした。
BとCは15人目の評価が2通りのままでしたし、DとEに至っては後半で確定するのかと思いきや、結局最後まで決まらずでしたね。
このように、最終的な結論が一通りに決まらない問題というのは、特に国家総合職ではかなり多く見られます。
その場合は、あり得る結果が2通り(あるいはそれ以上)ある中で、「確実に正しい記述」を選ぶことになります。
本問であれば、BとC、あるいはDとEの得点は確定しないので、これらに関する選択肢は全て×となります。
くれぐれも、一通りに決まらないからといって、途中でミスをしたのだと早合点しないようにしましょう。
2パターンくらいなら、最後まで残るのは国家総合職の判断推理では割とあるあるです。
2パターンくらいまで絞れて、かつ正解と思われる選択肢が選べるのであれば、きちんとできている可能性が高いので、あとは別の問題に時間を使う方が賢明です。
論理的に思考した結果であれば、あとは自分を信じましょう!
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
社員の持ち点は1人あたり15点であるから、13人目まででは15×13=195
この195点を、A〜Eに割り振ることになる。
13人目までのDとEの合計点を合わせたものは195-(40+39+35)=82点
合計が82であるような2つの整数の選び方は、次のようなものがある。
| 41 | 42 | 43 | 44 | 45 |
| 41 | 40 | 39 | 38 | 37 |
| × | × | ○ | × | × |
このうち、条件「同率の(合計点が一致した)観光地はなかった」および「1位と5位の合計点の点差は10点未満」より、組み合わせ(41, 41)、(42, 40)、(44, 38)、(45, 37)が消え、DとEの合計点の組み合わせは(43, 39)に決まる。
ただし、DとEのどちらが43点(または39点)であったか、というのは確定しない。
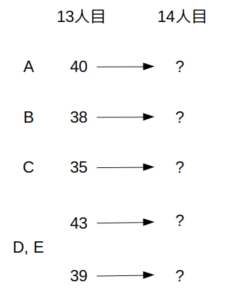
13人目までの合計点
次に、条件「14人目までの社員の評価を集計すると、同率の観光地がCを含めて3つあった」について、Cは13人目の時点では35点であるから、14人目の評価を加えた合計点は36〜40点の間となる。
このうち、36点または37点または38点または39点では、3人が同率となるのは不可能なので、Cを含む3人が同率で40点であったと分かる。
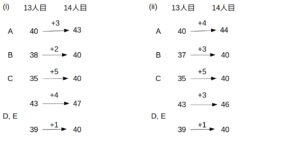
14人目までの合計点
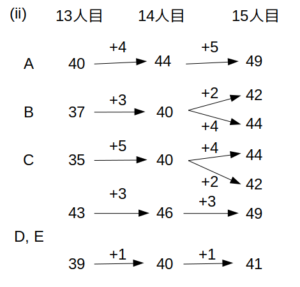
図は、14人目によってAに与えられた点が(i)3点の場合と(ii)4点の場合について、合計点の変化を書き出したものである。
これら2パターンについて、条件「14人目の社員と15人目の社員は、DとEに対しそれぞれ同じ点数を付けた」を適用すると次のようになる。
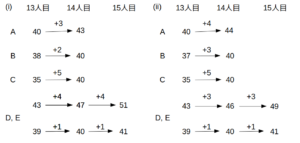
DとEに加点
条件「15人目までの社員の評価を集計し、最終得点を求めたところ、同率の観光地が2つあった」について。
「A+2=(B or C)+5=45」であれば条件を満たす。

(i-a)B+5または(i-b)C+5が条件を満たす
また(ii)は、15人目によるAの評価が5点であれば条件を満たす。
A〜Eの評価の合計点
以上より、確実に正しいといえるのは、4の「最終得点が同率の観光地の一方はAであった。」である。
したがって、正解は4である。

コメント
195-(40+39+35) の計算結果は82ではなく81なので考察の最初の前提が間違っています
私がこの問題について考えたABCDEの得点の組み合わせは
(49,41,44,42,49)
(49,44,41,42,49)
(45,44,45,42,49)
(45,45,44,42,49)
(48,41,45,43,48)
(48,45,41,43,48)
(45,44,45,43,48)
(45,45,44,43,48)
の8通りになりました。
コメントありがとうございます。
ご指摘の通り、195-(40+39+35)=81でしたので、前提条件を変えてBの得点を39点→38点としました。
これに伴い、選択肢1の文言および解説の内容にも若干の変更がありましたので、あわせてご確認ください。
また何かあればお気軽にコメントください!
コメント失礼します。
場合分け(ⅰ)について質問させていただきたいです。
>ここで、条件「15人目までの社員の評価を集計し、最終得点を求めたところ、同率の観光地が2つあった」を考えてみます。
まず認識すべきなのは、14人目の時点で同率だった3人は、15人目の評価によって必ず異なる合計点になる、ということです(社員はA〜Eにそれぞれ異なる点数を付けるから)。
つまり、15人目までの集計で同率となった2つの観光地とは、Aと「13人目までの合計点が43点だった観光地」、ということになります。
とありますが、場合分け(ⅰ)について、
15人目がAに2点、BまたはCに5点をつけると、条件「15人目までの社員の評価を集計し、最終得点を求めたところ、同率の観光地が2つあった。」を満たすのではないでしょうか。(AとB or Cが45点で同率)
もし、この指摘が正しいならば、選択肢「1.Aの最終得点は49点であった。」が確実に言えなくなります。
私が条件を見落としている可能性もあるのですが、ご確認いただけますと幸いです。
ご確認ありがとうございます
がんばってますね
Aと(BかC)が一致するパターンを見落としていたようです。
確かに、これだとAは1つに決まりませんね。
選択肢を変えて、なかったことにしときました。
引き続き、当サイトをご活用ください。