コンビニおにぎりと対応関係

こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます！
本ブログ、「数的処理の穴場」を運営しておりますモクセイと申します。

前回は、確率の小問を集めた複合的な問題を解きましたね。
数的処理に限らず、ふとした瞬間に勉強した内容を思い出すのは有効ですよ！
人間の脳は使わない記憶から忘れていくようにできているので、日常の中で思い出す機会があると定着しやすくなるんです。
昨日の晩ご飯が何だったかすぐに忘れてしまうのも、思い出す機会がないからですよね。
前置きもそこそこに、今日の問題に移りましょう！

演習問題：コンビニおにぎりと対応関係

「誰が」「何のおにぎりを」「どこで」買ったのかを明らかにする必要があります。
以前の記事で似た問題を扱ったときは、条件を整理しながら表を作成しましたね。
今回も、対応関係の問題として表を作っていく方針が良いでしょう。
以下、この問題を詳しく解説していきますが、回りくどいのが苦手な方は一番下の略解だけ読むのもアリです。

それではスタート！

詳しい解説

前提条件として、
「（各店舗は）4種類のおにぎりを1個ずつ販売し、買えるおにぎりの個数を1人1個までとしている」
および
「4人は4つの店舗をはしごして異なる味を一つずつ、それぞれ計4つのおにぎりを購入する」
とあります。
これらのことから、誰かのおにぎりが1つ定まるごとに、以下の2点の事実が明らかになります。

• 他の人が同じお店で同じおにぎりを買うことはない
• その人が同じお店で他のおにぎりを買うことはない

例えば、Aが「東」で梅おにぎりを買ったことが分かれば、他の人が「東」で梅おにぎりを買った可能性が消えるし、Aが「東」で梅以外のおにぎりを買った可能性もなくなります。
以下のような表を作ると、○を付けた上下左右の一列全てに×が付けられます。

	東
	梅	しゃけ	昆布	おかか
A	○	×	×	×
B	×
C	×
D	×

○1つに対して×が6個も付く、というのはかなりオイシイ。
これを利用しましょう。
以下、次のような表を用意し○×を記入していきます。

	東				西				南				北
	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか
A
B
C
D

まず、
条件ア「Dは「東」シールの付いた梅おにぎりを買った」
および、条件ウ「「北」シールの付いた昆布おにぎりを買ったのはBではない。」をそのまま記入します。

	東				西				南				北
	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか
A	×
B	×														×
C	×
D	○	×	×	×	×				×				×

アより、A〜Cは東で梅おにぎりを買うことはなく、かつD自身も東では他のおにぎりは買わないので、東の縦横一列に×が入ります。
加えて、Dは他のお店で梅おにぎりは買わないので、西南北の梅にも×が入ります。

次に、条件エ「Cが買った梅おにぎりに付いていたシールと、Aが買ったおかかおにぎりに付いていたシールは同じだった」を考えます。
Cは東では梅おにぎりを買っていないので、「Aが買ったおかかおにぎりに付いていたシール」は東以外の何か、となります。
これより、Aの東のおかかおにぎりは×。

同じように、条件オ「Dが買ったしゃけおにぎりに付いていたシールと、Cが買ったおかかおにぎりに付いていたシールは同じだった」について、Cも東シールのおかかおにぎりを買っていないことが分かります。（Dは東のしゃけは×）

	東				西				南				北
	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか
A	×			×
B	×														×
C	×			×
D	○	×	×	×	×				×				×

すると、消去法により東でおかかおにぎりを買ったのはB、ということになります。
→B東の残り２つ＆他のおかかは×

	東				西				南				北
	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか
A	×			×
B	×	×	×	○				×				×			×	×
C	×			×
D	○	×	×	×	×				×				×

条件イによれば、「東で昆布おにぎりを、西でしゃけおにぎりを買った者」がいるが、それはCではない、とのこと。
ここまでの表によれば、C東はしゃけ or 昆布。
→C東は（昆布ではない方の）しゃけに決まります。
ついでに「東で昆布おにぎりを、西でしゃけおにぎりを買った者」はAだったと決まります。

ここまでの表は以下。

	東				西				南				北
	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか	梅	しゃけ	昆布	おかか
A	×	×	○	×	×	○	×	×		×	×			×	×
B	×	×	×	○	(i)	×		×				×			×	×
C	×	○	×	×	(ii)	×				×				×
D	○	×	×	×	×	×			×				×

ここからは西で梅を買ったのが(i)Bなのか、(ii)Cなのかで場合分けして考えます。

(i)西の梅がBの場合
Bの他店の梅は×（→西の梅の列はB以外×）
すると、Bの北はしゃけしかありません（→縦一列は×）

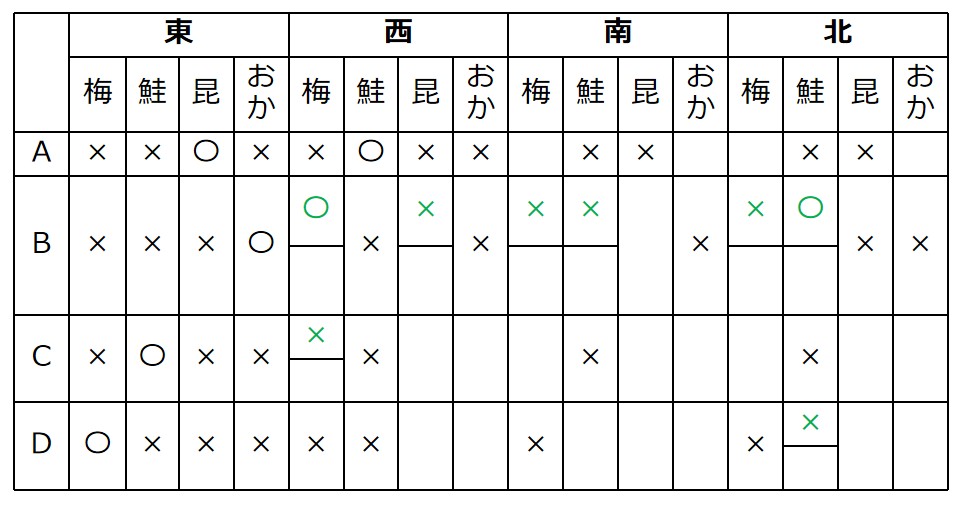
Bの南も、消去法で昆布が〇になります（→南の昆布の列はB以外×）

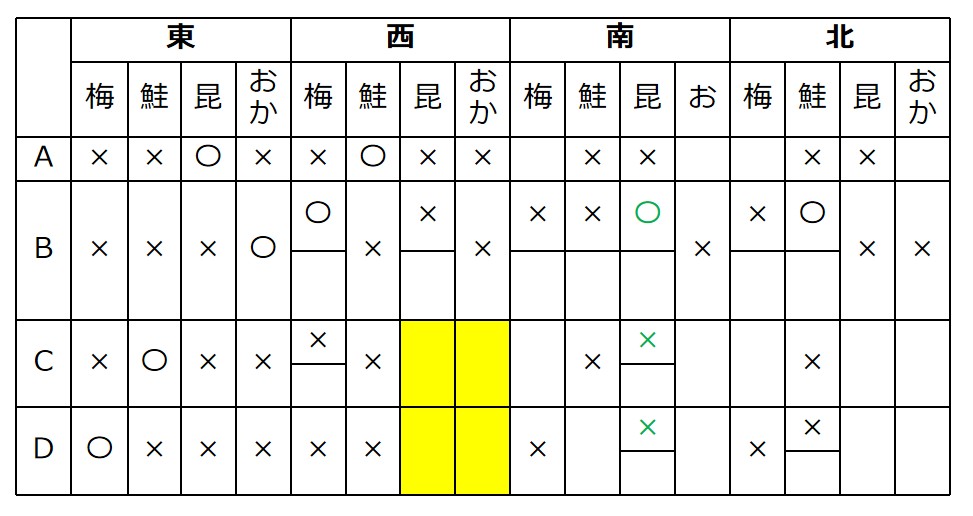
次に、西のCとD（黄色いエリア）について。
Cは昆布またはおかかですが、条件オ「Dしゃけ＝Cおかか」を満たすには、C＝昆布とするしかなく、D＝おかかに決まります。
（C＝おかか、としてしまうとD＝昆布がオに反する ）

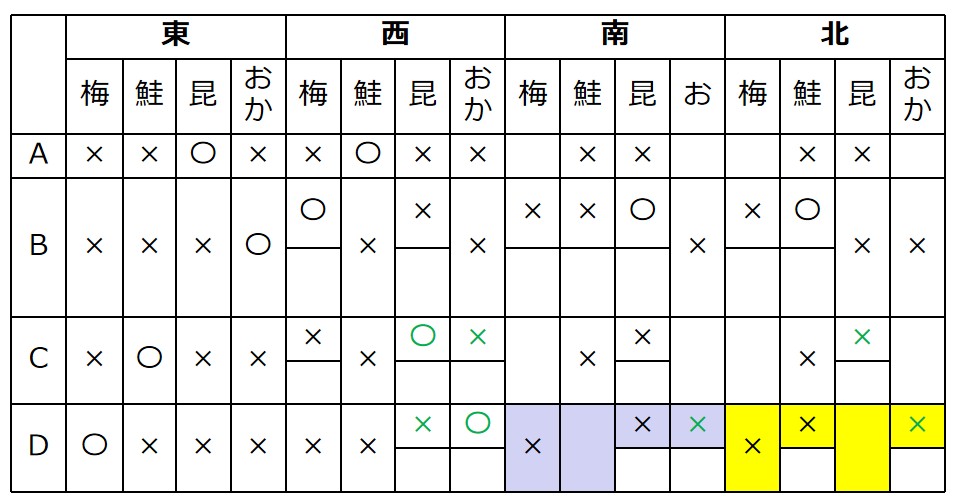
Dの南北（青と黄）に注目。
南はしゃけ、北は昆布、と決まります。
→条件オ「Dしゃけ＝Cおかか」より、Cの南はおかか

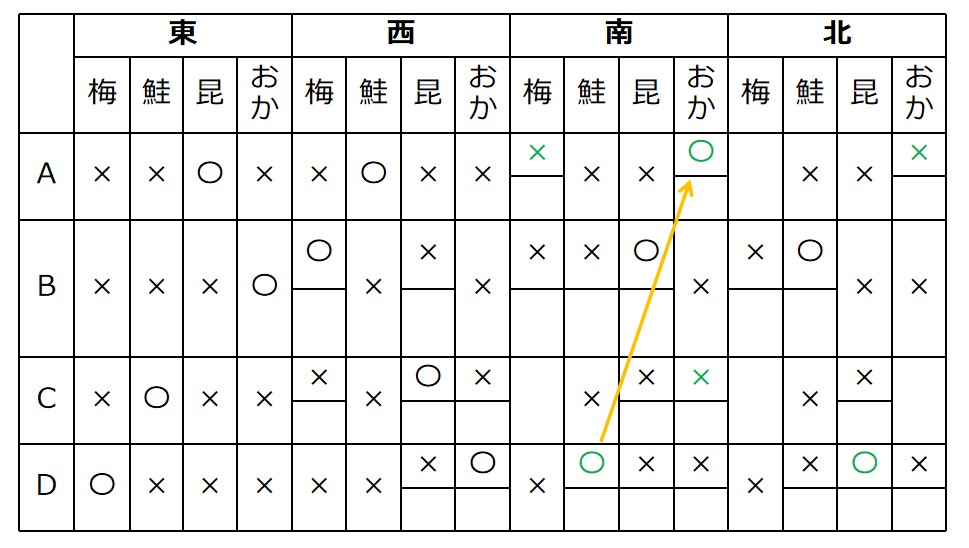
Aの北は梅に決まり、芋づる式にCの南北も決まります。
→(i)の表が完成

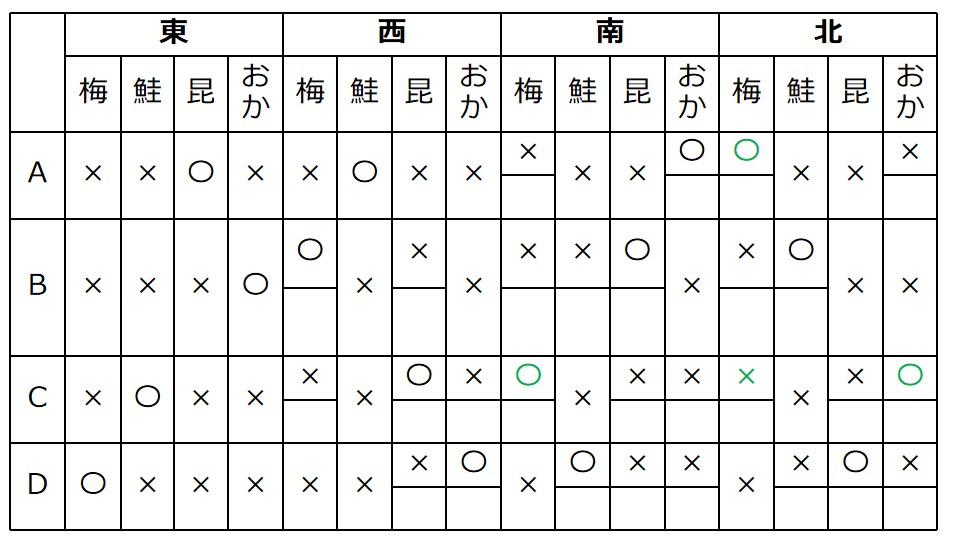
(ii)西の梅がCの場合
Aの西はしゃけ（≠おかか）だったことを思い出します。
条件エ「C梅＝Aおかか」を満たさないので、この場合は不適。

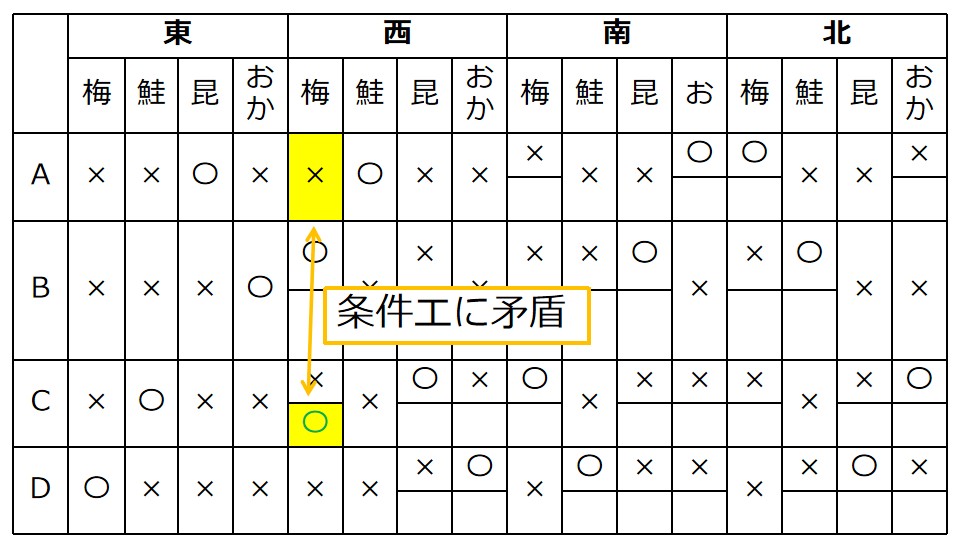
以上より、１が正解となります。

おわりに

お疲れ様でした！
いかがだったでしょうか？

「誰が（A〜D）」「何を（おにぎり）」「どこで（お店）」の3要素が絡んだ対応関係の問題でした。
対応関係の問題では、まず表を用意して与えられた条件から分かることを書き込んでいく、というのがよく知られた解法です。
表のフォーマット（何を縦に、何を横に並べるか）を適切に設定できるかどうか、という点がその後の明暗を分けます。
今回だと、前項の最後にあるような、A〜Dを縦に、東西南北を横に並べたフォーマットも考えられます。
これでも解けないことはないですが、私は本問では解説にあるような、○×を書き込む形式を用いることをおすすめします。
○×形式の方が、「〜でない」という否定の情報も可視化できるからです。
実際、本問は消去法で情報が確定する場面が多かったので、このフォーマットが大いに役立ちました。
ただし、情報量が多いということは、その分必要な情報を見失いやすいということでもあるので、結局は状況に応じてフォーマットを使い分けるしかない、というのが実情だと思います。
国家総合職の数的処理において、対応関係はド定番ともいえるテーマです。
毎年1問は必ず出題されるので、ここをおろそかにすると数的処理の得点が伸びません。
適切な表さえ用意できれば、あとは条件から分かることを書き込んでいくだけです。
条件を表に落とし込むと新たな情報が得られるので、そこから分かることをまた表に書き込んで……という作業を繰り返せば、きちんと正解にたどり着きます。
いろいろな対応関係の問題を解いて、まずは条件を表に整理できるように練習しましょう！

本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！

次回もお楽しみに！