【国家一般職】大丈夫？「全体量１」のワナ。仕事算は単位を意識して【ペンキ塗り作業の仕事算】

こんにちは！
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。

公務員試験を受ける方は必見！
ぜひ最後まで読んでいってください。

今回のテーマは……「仕事算（方程式）」

仕事算の解き方といえば、「全体量を１とおく」
これ、すごく抽象的で分かりづらいなーと筆者は思うんです。

実は、仕事算の全体量は必ずしも１とする必要はありません。
生産数１００台とか、コピー用紙１０００枚とか、具体的な数だっていいんです。
仕事算は、【仕事量に単位を与える】と圧倒的に式が立てやすくなります。

今回は、【仕事量に単位を与える】と仕事算をもっと理解できるよ、というお話です。

例によって、数的処理の過去問みたいな演習問題を使ってレクチャーします。

演習問題：ペンキ塗り作業の仕事算

ペンキ塗り作業を分かち合う問題。
一定の広さってどれくらい？

以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。

おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

それでは、解説スタート！

問題文を見る

解説：壁の広さを枚数で表現する

決まった量を、数人で協力して減らしていってゼロにする、という問題を「仕事算」といいます。

ニュートン算の解き方は、以前紹介しています。

この流れに沿って進めます。

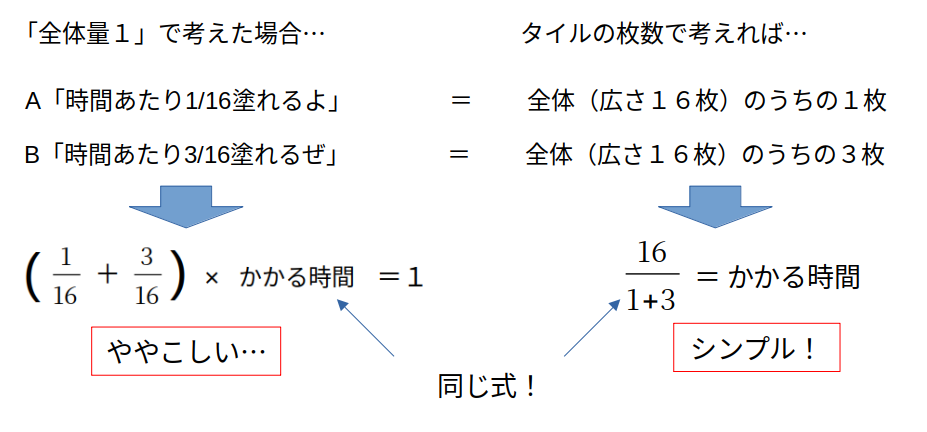
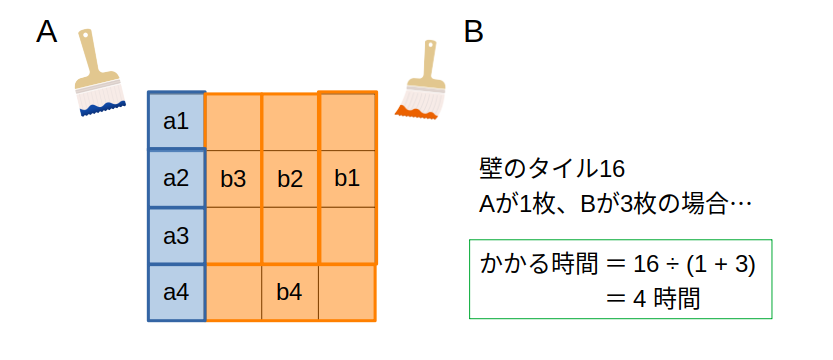
【１】文字でおく：仕事量をタイルの枚数でとらえる

仕事算は、【仕事量に単位を与える】と解きやすくなります。

仕事量に、単位を付けてあげてください。
本問であれば、「壁の広さ」

仮に、\(n\)枚のタイルでできた壁、と考えてみます。
このとき、AとBが時間あたりに塗るタイルの枚数は、単純な足し算（\(a+b\)枚）で与えられます。

すると、かかる時間は割り算で求められます。
文字で表せば、\(\frac{n}{a+b}\)

【２】式を立てる：仕事にかかる時間の条件を式化

「５人全員でペンキを塗ると、ちょうど１時間で塗り終えられる」のであれば、

\[
\frac{n}{a+b+c+d+e}=1…(\mathrm{o})
\]

１つ目の条件「AとBの２人でペンキを塗ると、塗り終えるのに\(\frac{27}{10}\)時間かかる。」より、

\[
\frac{n}{a+b}=\frac{27}{10}…（\mathrm{i}）
\]

２つ目の条件「AとCの２人でペンキを塗ると、塗り終えるのに\(\frac{12}{5}\)時間かかる。」より、

\[
\frac{n}{a+c}=\frac{12}{5}…（\mathrm{ii}）
\]

３つ目の条件「BとCの２人でペンキを塗ると、塗り終えるのに4時間かかる。」より、

\[
\frac{n}{b+c}=4…(\mathrm{iii})
\]

【３】連立：辺々足すと「\(a+b+c=〜\)」ができる

（i）＋（ii）＋（iii）より、

\[
2(a+b+c)=\frac{28}{27}n \\
→a+b+c=\frac{14}{27}n
\]

これを（o）に代入すると、

\begin{align}
\frac{14}{27}n+&d+e=n \\
&→d+e=\frac{13}{27}n \\
&→\frac{n}{d+e}=\frac{27}{13}…（答）
\end{align}

よって、２が正解です。

おわりに：仕事算は単位で理解する

お疲れ様でした！

仕事算では、【仕事量に単位を与える】と理解して式を立てられるのでおすすめです。
仕事算に限らず、文章題は数量同士の関係をつかむのが大切ですよ。

今回は、一定量の仕事を分担したときにかかる時間の問題でした。
壁の広さをタイルの枚数で捉えると、分担した場合の時間の関係が見えやすくなります。

解き方はニュートン算と全く同じ。
収支でとらえるなら、はじめの量\(n\)に対し、収支が\(a+b\)ずつマイナス、と解釈できます。

ニュートン算の「解法のポイント」について、もっと知りたい方はコチラ（やや難）

こっちは標準レベル。

最後までお読みいただきありがとうございました。

本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！

この記事が参考になったら、ぜひシェアしてください！

Tweet

次回もお楽しみに！

略解