【国家総合職】正誤の判定結果から4桁の数字列を推測する問題と解説

こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます！
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。

これまで国家総合職の過去問に的を絞って解説してきましたが、特にここ最近はネタが尽きかけてだいぶ個別性の高い（＝他の問題に応用しづらい）問題ばかりになってきてますね。
受験する皆さんのことを考えると、そろそろ総合職を離れて、他の区分からもっと汎用性の高い問題を持ってくる方が有益なんだろうか、とか考え中。
需要からいって、国家一般職あたりの過去問の解説に移るのが良さげかなぁ。

前回は、サイコロの出目によって移動する駒がゴールにたどり着く確率を求める問題でした。
数的処理の頻出分野、確率の問題です。
ぜひ解いてみてください。

もう解いた方は、お疲れ様でした。
新しい問題に触れるのと同じかそれ以上に、復習は重要です。
復習するときは、

「他の問題に使えそうな知識は何かな？」

と考えながら解説を読み込んでみてください。
本試験では過去問と全く同じ問題は出ないので、解いた問題に「似た」問題に対処する必要があると言えます。
解いた問題から得た知見をもとに、初見の問題を処理するのです。
目の前の問題に近しい問題を攻略することを想定しながら、数的処理の勉強を進めていってください。

復習がバッチリな方は、本日の問題へ参りましょう！

目次（※演習問題のネタバレ注意）

本日の演習問題
詳しい解説
おわりに
略解

本日の演習問題

1〜9のうちから異なる数を無作為に4つ選出し、4桁の自然数（以下「M」とする）を新たに生成する装置がある。この装置に4桁の数字（以下「N」とする）を入力すると、MとNの数字を各桁ごとに比較し、以下に示す「判定基準」にしたがって○、△、×のいずれかの記号を返す機能が備わっている。

判定基準：
○…比較した桁と数字がともに一致したとき
△…桁は異なるが他の桁に一致する数字があるとき
×…比較対象の数字が他のいずれの桁の数字とも異なるとき

例えば、M=1234、N=1345のとき、返される記号は次のようになる。
「○1（千の位の数字が一致）、△2（3と4は桁は異なるがMにもNにも存在する）、×1（5はMのいずれの桁にも存在しない）」

いま、この装置に一度だけMを生成させたあと、以下の4つの自然数Nを入力したところ、記号は以下の通りであった。

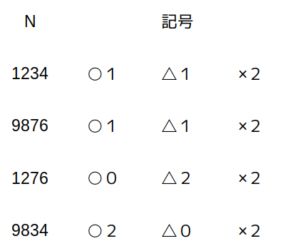
このとき、Mとして考えられる数のうちで最大のものと最小のものの差はいくらか。

6895
5273
4995
3968
2918

１

4桁の整数を当てる問題です。
条件に合う整数は複数個あることになります。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。

それではスタート！

詳しい解説

入力した数字列と判定結果を、次のようにラベリングします。

1234（○1、△1、×2）……(i)
9876（○1、△1、×2）……(ii)
1276（○0、△2、×2）……(iii)
9834（○2、△0、×2）……(iv)

いきなり4桁全ての数字を当てようとするのは大変なので、左右で半分に分けて2桁ずつ考えましょう。
（入力した数字列を見比べて、右あるいは左半分の2桁が一致するペアが作れる、というところから発想してほしい）

まず、(i)と(iii)を見比べます。
数字の変化がある右半分の2桁に注目です。
ここが「34」→「76」と変化したことによって、判定結果には○が1つ減り△が1つ増える、という変化が起こっています。
ここから得られる情報は次の2つです。

3と4のうち一方のみ○（数字列は□□3□あるいは□□□4の形）
7と6のうち一方のみ△

次に、(ii)と(iii)を見比べます。
同じように、変化のあった左半分の2桁に注目します。
ここが「98」→「12」と変化したことで、判定結果には○が1つ減り△が1つ増える、という変化が起こっています。
ここから得られる情報は次の2つです。

9と8のうち一方のみ○（数字列は9□□□あるいは□8□□の形）
1と2のうち一方のみ△

○に関する情報から、Mとして考えられる数字列は以下の4パターンに限られます。

9□3□
9□□4
□83□
□8□4

ここに△に関する情報を加えると、各々2つある□のうち、一方には1 or 2、他方には7 or 6が、それぞれ入ることになります。

以上の制約に基づいて、ありうる数字列のうち最大のものと最小のものを探し、差を求めます。

まず最大値を求めます。
最大値になりうるのは、上の4パターンの中では「9□3□」か「9□□4」のいずれかです。
（あとの2パターンでは、先頭の桁に来る数字は9以外なので最大とはなり得ません）
欲しいのはあくまで最大値なので、2つの□には「2」と「7」を入れましょう。
可能な数字列として「9732」と「9724」がありますが、大きいのは前者でこれが最大です。

次に最小値を求めます。
今度は「□83□」と「□8□4」が対象です。
できるだけ小さい数字列がほしいので、2つの□には「1」と「6」を入れる……としたいところですが、ちょっと待ってください。
この場合、先頭の桁を「1」とすることになりますが、それは(i)と(iii)に反します。
よって、先頭の桁は「2」とする必要があります。
できる数字列は「2836」と「2864」ですが、前者は(ii)に反します。
（8と6で○が2つあることになる）
これより、一の位を「6」ではなく「7」とした「2837」が最小です。

以上より、求める差は9732-2837=6895

よって、１が正解です。

おわりに

お疲れ様でした！
いかがだったでしょうか？

ランダムに自然数を生成する装置の出力をもとに、4桁の数字列を当てる問題でした。
装置が生成した文字列を一意に決めるのではなく、制約条件を満たす中から最大および最小のMを探す、というのが主旨でした。
判断推理のように始めから条件が明確に与えられるわけではなく、出力をヒントに自力で推測しなければならないところに難しさのある一問です。
左右2桁ずつに分けて順番に考察するのがポイントです。
入力された数字列の類似性からこの発想にたどり着きたいところ。

h https://suuteki-no-anaba.com/count-natural-number/

本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！

この記事が参考になったら、ぜひシェアしてください！

次回もお楽しみに！

略解

1234（○1、△1、×2）……(i)
9876（○1、△1、×2）……(ii)
1276（○0、△2、×2）……(iii)
9834（○2、△0、×2）……(iv)

(i)と(iii)を比べると、右半分の2桁が「34」→「76」と変化したことで、判定結果は○が1つ減り△が1つ増えている。
ここから得られる情報は以下の2つである。

3と4のうち一方のみ○（数字列は□□3□あるいは□□□4の形）
7と6のうち一方のみ△

次に、(ii)と(iii)について、左半分の2桁が「98」→「12」と変化したことで、判定結果は○が1つ減り△が1つ増えている。
ここから得られる情報は以下の2つである。

9と8のうち一方のみ○（数字列は9□□□あるいは□8□□の形）
1と2のうち一方のみ△

情報を総合すると、Mとして考えられるのは次の4パターンである。

9□3□
9□□4
□83□
□8□4

△に関しては、各々2つある□のうち、一方には1 or 2、他方には7 or 6が、それぞれ入ることになる。

これらをもとに、数字列の最大値と最小値を順に求める。

まず最大値について、最大値になりうるのは「9□3□」か「9□□4」のパターンである。
かつ、2つの□には「2」と「7」が入ることになる。
可能な数字列として「9732」と「9724」があるが、最大なのは明らかに前者である。

次に最小値について、可能性があるのは「□83□」と「□8□4」である。
先頭の桁を「1」としてしまうと(i)と(iii)に反するから、先頭の桁は「2」でなければならない。
もう一方の□を「6」とすると、できる数字列は「2836」と「2864」だが、前者は(ii)に反する。
これより、一の位を「6」ではなく「7」とした「2837」が最小となる。

以上より、求める差は9732-2837=6895

したがって、１が正解である。