こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「軌跡(平面図形)」
軌跡はイメージが大切。
移動する点なり、図形なりの動きを正しく捉えることが必要です。
以前、回転する図形をイメージするコツを紹介しました。
- 小さなステップに分ける
- 回転の中心、半径、回転角を押さえる
- 繰り返し(対称性)にも注意
このポイントが有効なのは、点の軌跡だけではありません。
線や図形の移動を考える場合にも有用です。
今回は、回転移動の軌跡をイメージしやすくする「解法のポイント」を、数的処理の過去問みたいな演習問題を使ってレクチャーします。

過去問に近いレベルになってます
演習問題:転がる棒が通過するエリアの面積
図1のような階段状の図形の上に、長さ4の細い棒を置く。この棒が、図2のような状態から時計回りに滑ることなく回転し、点Gに接するまで移動する。このとき、棒が通過する領域の面積に最も近い値は次のうちどれか。
ただし、一辺の長さが1である正三角形の高さは0.86、円周率は3とする。
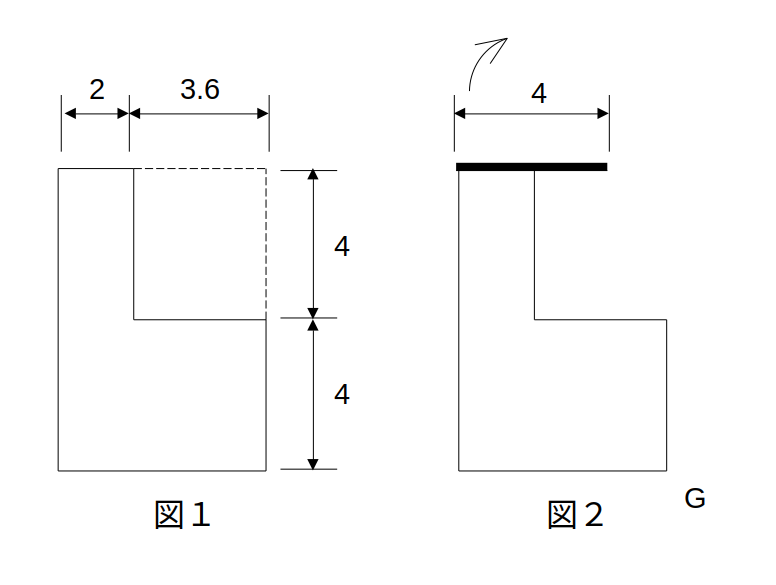
転がる棒の通過領域は?
- 40
- 50
- 60
- 70
- 80
1
通過領域の面積の問題。
形をイメージすること。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:ステップごとの中心&半径&回転角を知る
面積を求めるなら、まずは通過領域がどんな形かを知る必要があります。
Q:どうやって?
A:描いてみるしかありません。
滑らずに転がる軌跡の「解法のポイント」を意識して、回転の様子をイメージします。
- 小さなステップに分ける
- 回転の中心、半径、回転角を押さえる
- 繰り返し(対称性)にも注意
ふつう、軌跡といえば点の移動ですが、動くものが線や図形であっても考え方は同じ。

ステップの区切り方が分からないよドラえも〜ん
回転移動のステップは、回転の中心や半径が変わるタイミングで区切るのがセオリー。
中心や半径が変わらない間は扇形(円弧)なので、面積や長さを計算できる、というわけです。

だれが正月太りで「身長体重胸囲129.3cm」じゃ
この観点によると、本問は3つのステップに分けることができます。
説明のため、棒の左端をA、右端をB、中点をPとします。
Step1:点Pを中心とする90°回転
点Pを中心に転がって、垂直な壁にくっついて止まる動きをイメージします。
半径PAの90°回転で、扇形の通過領域ができます。
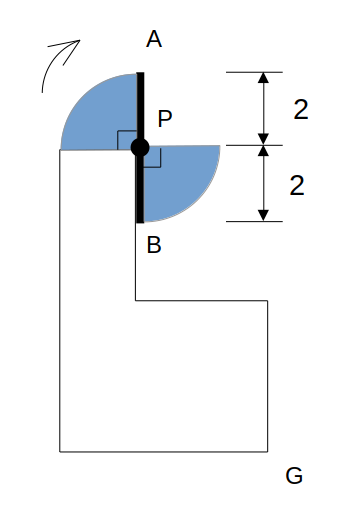

PBの通過領域はあとで重ね塗りされるので考えなくてOK
この間の通過領域の面積は、
\[
\pi × 2 × 2 × \frac{90}{360} = \pi……(\mathrm{i})
\]

円周率は\(\pi\)としておいて最後に計算します
Step2:点Bを中心とする120°回転
垂直な壁から、時計回りに回転する様子をイメージします。
点Bは常に接したまま、点Aが次の段にぶつかって回転が止まります。
このとき、棒は壁に立て掛けた状態です。

Bを中心とした、半径BAの回転
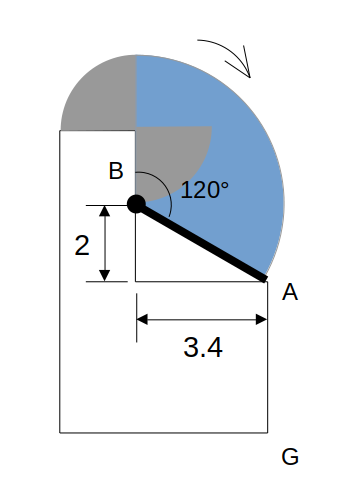
立て掛けた棒の下の隙間に注目。
ここは直角三角形で、斜辺と短辺の比は2:1。
ということは……
「30°、60°、90°の直角三角形」
これより、棒の回転角は120°だった、と分かります。

底辺の長さは3.4なので、Aはちょうど段の角
通過領域の面積は、
\[
\pi × 4 × 4 × \frac{120}{360} = \frac{16}{3}\pi……(\mathrm{ii})
\]
Step3:点Aを中心とする240°回転
立て掛けた状態から時計回りに回転するとき、点Aは固定されます。
Aを中心とした、半径ABの回転をイメージします。
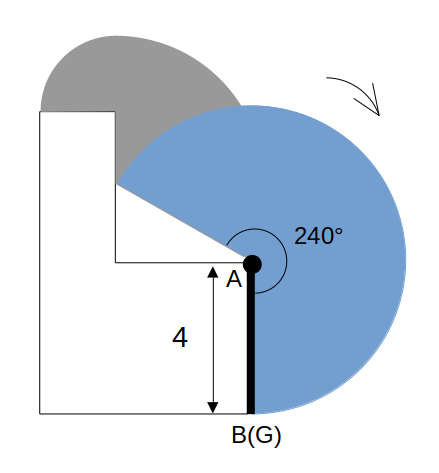
棒は壁にぶつかって止まります。
回転角は、360°ー(90°+30°)=240°
通過領域の面積は、
\[
\pi × 4 × 4 × \frac{240}{360} = \frac{32}{3}\pi……(\mathrm{iii})
\]
あとは、(i)、(ii)、(iii)を足し合わせるだけ。
…というわけにはいかず。
重ね塗りされた部分の面積の分を補正する必要があります。

もうちょっとだけ続くんじゃ
延長戦:重なった部分の面積を求める
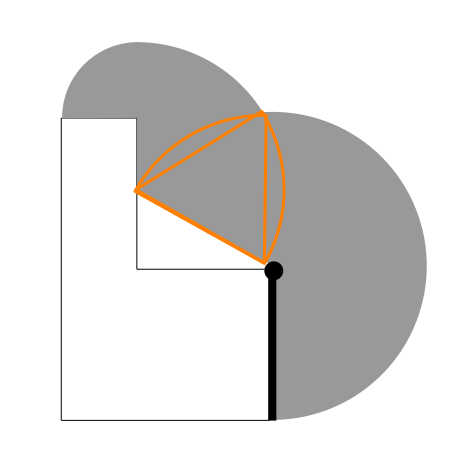
重ね塗りの部分をオレンジ色で示しました。
この部分を二重に数えてしまうので、引き算する必要があります。
さて、どうやったら求められるでしょう?
この図形の成り立ちにヒントがあります。
そもそもこの領域は、扇形を重ね塗りしたものでした。
であれば、ここも足し合わせて共通部分(三角形)を引き算すればOK。

もしかして:正三角形
つまり、
オレンジの面積=扇形+扇形ー正?三角形
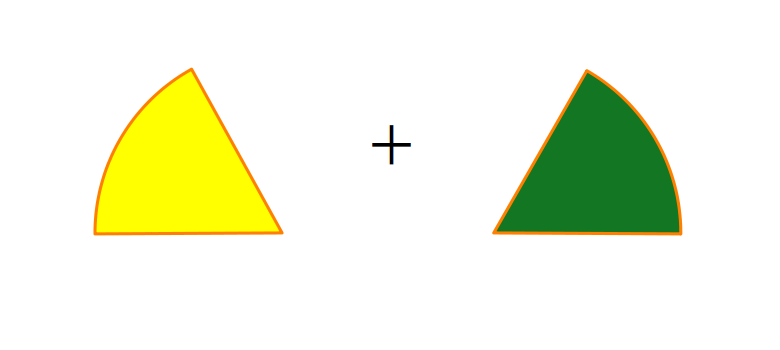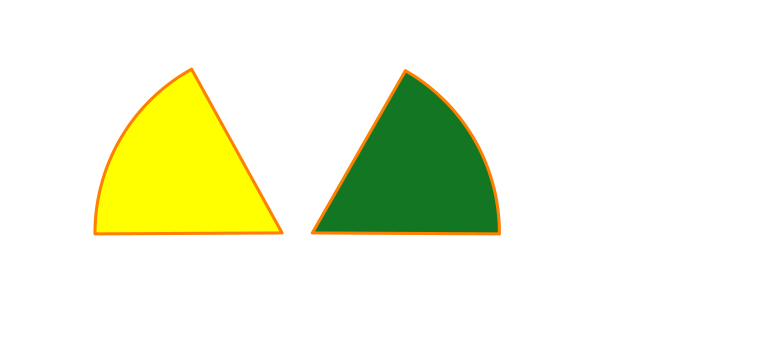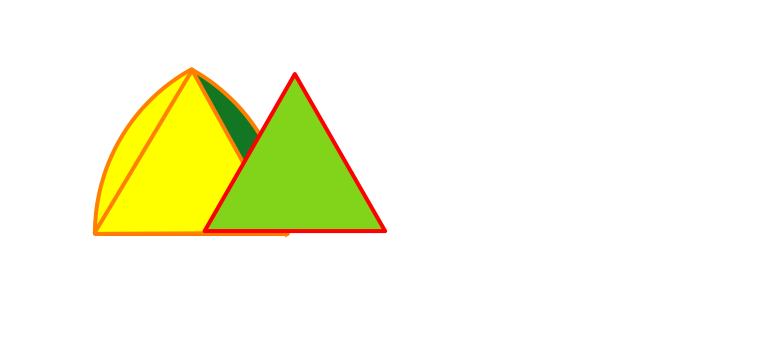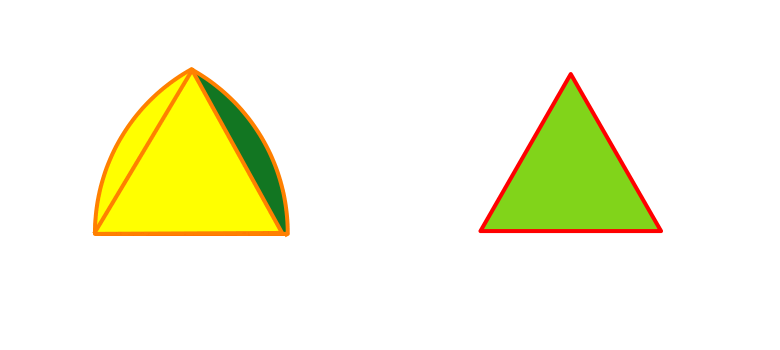
まず、正?三角形について。
この三角形の各辺は全て、棒ABが通ってきた「足あと」です。
ということは、長さは全て4。
まさしく、一辺の長さ4の正三角形。
すると、扇形は「半径4、中心角60°」
面積は、
\[
\pi × 4 × 4 × \frac{60}{360} = \frac{8}{3}\pi
\]
正三角形については、「一辺の長さが1である正三角形の高さは0.86」を使って求めます。
一辺が4なら、高さは0.86×4=3.44
→(正三角形)=4×3.4÷2=6.88
よって、オレンジの図形の面積は、
\[
\frac{8}{3}\pi+\frac{8}{3}\pi-6.88=\frac{16}{3}\pi-6.88
\]
以上より、棒が通過する領域の面積は、
\begin{align}
(\mathrm{i})+&(\mathrm{ii})+(\mathrm{iii})-(橙) \\
&=\pi+\frac{16}{3}\pi+\frac{32}{3}\pi-(\frac{16}{3}\pi-6.88) \\
&=\frac{35}{3}×3+6.88 \\
&=41.88
\end{align}
選択肢を見ると、この値に最も近いのは1の「40」。
よって、1が正解です。
おわりに:転がる軌跡は中心&半径&回転角で決まる
お疲れ様でした!
滑らずに転がる図形の軌跡は、まず「イメージ」すること。
意識するポイントは3つ。
・ステップに分ける
・回転の中心、半径、回転角
・対称性
ステップに分けるときは、扇形に注目するのがコツ。
半径(中心)が固定なら、転がる移動の軌跡は扇形(円弧)です。
なので、半径や中心が変わるタイミングで区切れば、全体は扇形の寄せ集めとして計算できます。

やっぱり中心と半径がカギ
今回は、滑らずに転がる棒が通るエリアの面積を計算する問題でした。
中心点が切り替わる瞬間を捉え、ステップごとに扇形の面積を求めて足し合わせます。
このときに重ね塗りの部分を2回数えてしまうので、引き算で補正します。
点の軌跡をもう1問。
回転つながり。
この正月のハイライトは、食後のぬるま湯で溺れかけたことでした

2025年、のっけからとんでもない年になりそうでワクワクしてる
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
点Pを中心にとした回転

Step1:Pを中心とした90°回転
垂直な壁にぶつかって止まる。
→半径PA=2、回転角90°の扇形
面積は、
\[
\pi × 2 × 2 × \frac{90}{360} = \pi……(\mathrm{i})
\]
点Bを中心とした回転

Step2:半径4、回転角120°の回転
傾いた棒の下側は、「30°、60°、90°」の直角三角形。
→半径BA=4、回転角120°の扇形
面積は、
\[
\pi × 4 × 4 × \frac{120}{360} = \frac{16}{3}\pi……(\mathrm{ii})
\]
点Aを中心とした回転

Step3:Aを中心とした240°回転
点BがGに一致して止まる。
→半径AB=4、回転角240°の扇形
面積は、
\[
\pi × 4 × 4 × \frac{240}{360} = \frac{32}{3}\pi……(\mathrm{iii})
\]
重なった領域(オレンジ色)の面積を求める。

重なった部分の面積は?
三角形の各辺の長さは4。
→正三角形
高さは0.86×4=3.44なので、面積は
4×3.44÷2=6.88
重なった扇形は「半径4、中心角60°」なので、面積は
\[
\pi × 4 × 4 × \frac{60}{360} = \frac{8}{3}\pi
\]
オレンジの面積は、「扇形+扇形ー正三角形」より、
\[
\frac{8}{3}\pi+\frac{8}{3}\pi-6.88=\frac{16}{3}\pi-6.88
\]
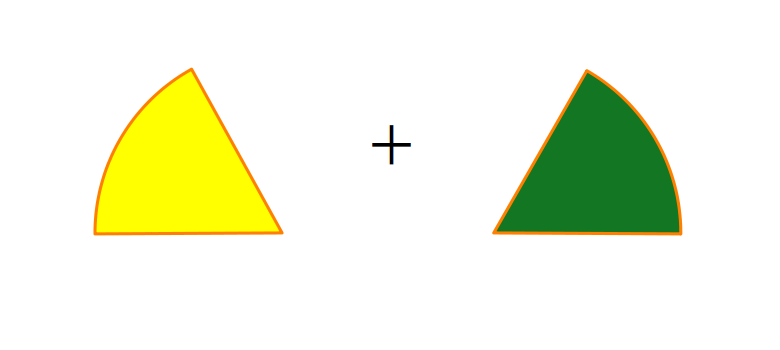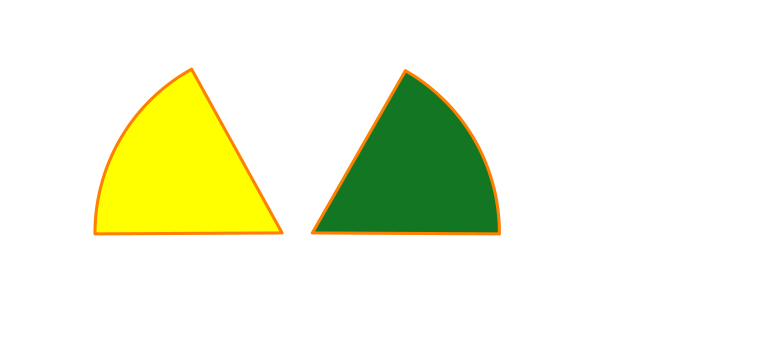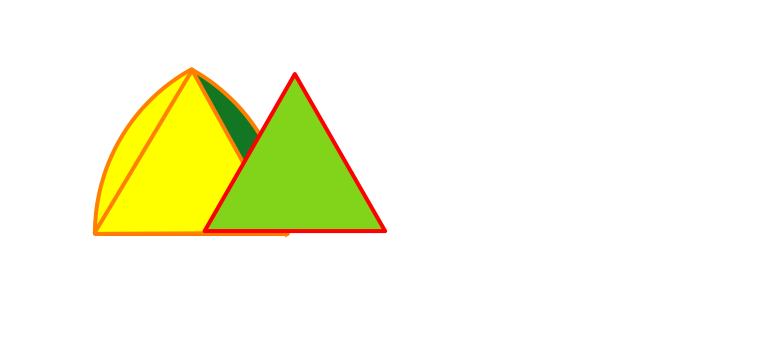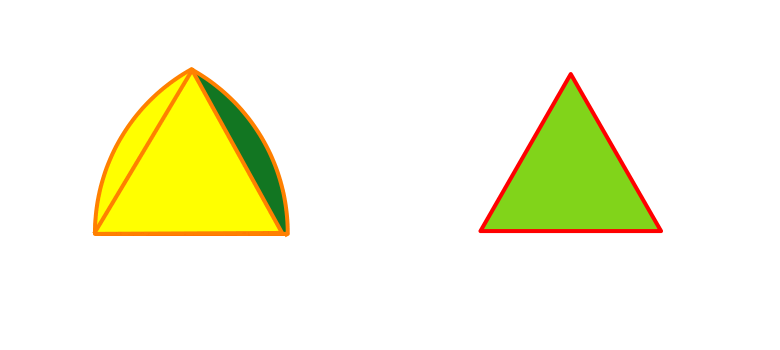
足し合わせたあと共通部分を引く
以上より、通過領域の面積は
\begin{align}
(\mathrm{i})+&(\mathrm{ii})+(\mathrm{iii})-(橙) \\
&=\pi+\frac{16}{3}\pi+\frac{32}{3}\pi-(\frac{16}{3}\pi-6.88) \\
&=41.88
\end{align}
したがって、1が正解である。







コメント
コメント失礼します。
>以上より、通過領域の面積は
(i)+(ii)+(iii)−(橙)=π+(16π/3)+(32π/3)−((16π/3)−6.8)=84.6
とありますが、16π/3が打ち消し合い、π+(32π/3)+6.8=3+(32/3)*3+6.8=41.8になるのではないでしょうか。
こちらが間違っている可能性も大いにあるのですが、ご確認いただけますと幸いです。
コメントありがとうございます。
ご指摘の通り、計算に誤りがあったようです
見直した結果、おおよそ40になりました
すばらしいお気づきです!
棒が通過する領域の面積の計算が間違っています
π+16/3π+32/3π-(16/3π-6.8) これは
35/3π+6.8 になるので、π=3より
35+6.8=41.8 になります
確認ありがとうございます!
おおよそ40、が正解でした
いつも的確なご指摘感謝いたします