こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「食塩水の濃度計算」
以前、食塩水の濃度計算をてんびん図で解くやり方を解説しました。
今回は濃度計算の基本にスポットを当て、「ここに注目すれば解ける」というポイントを紹介します。
てんびん図はあくまでテクニックで、こっちが本筋の解き方。
食塩水の濃度計算で注目すべきポイント。
それは……
【溶けている食塩の量】
まずは頻出の3パターンについて、簡単な例題を使って解き方を解説します。
後半では、数的処理の過去問みたいな演習問題を解きながら、その使い方を学んでいきます。

学校のテストと過去問の中間くらいのレベルです
講義:濃度計算は食塩の量に注目
食塩水の濃度計算問題は、【溶けている食塩の量】が超!重要。
混ぜ合わせる前後で、食塩水に溶けている食塩の量を計算します。
食塩の量=濃度(%)×食塩水の質量(g)
例えば、AとBを混ぜてCができた、という場合、食塩の量に関しては「A+B=C」となります。
そして、全体で見れば「混ぜる前」=「混ぜた後」です。

食塩水を混ぜても、溶けた食塩は消えないはず
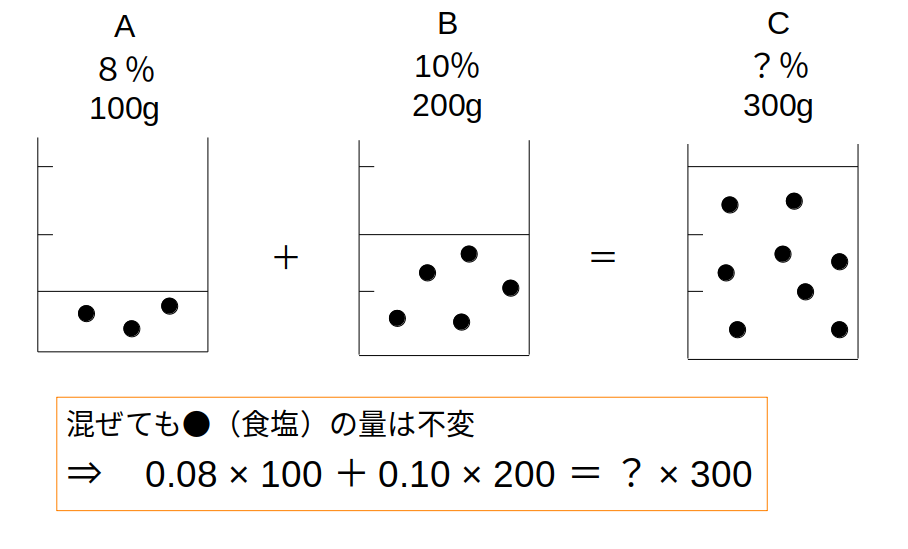
これは、水(or 食塩)を加える場合や、熱して蒸発させるような場合も同じ。
食塩の量に関していえば、「前」=「後」です。
以下、濃度計算の基本パターンである「混ぜる・薄める・蒸発」の3つを、
【溶けている食塩の量】を使って解いてみます。
【1】混ぜる:異なる濃度を混ぜ合わせるパターン
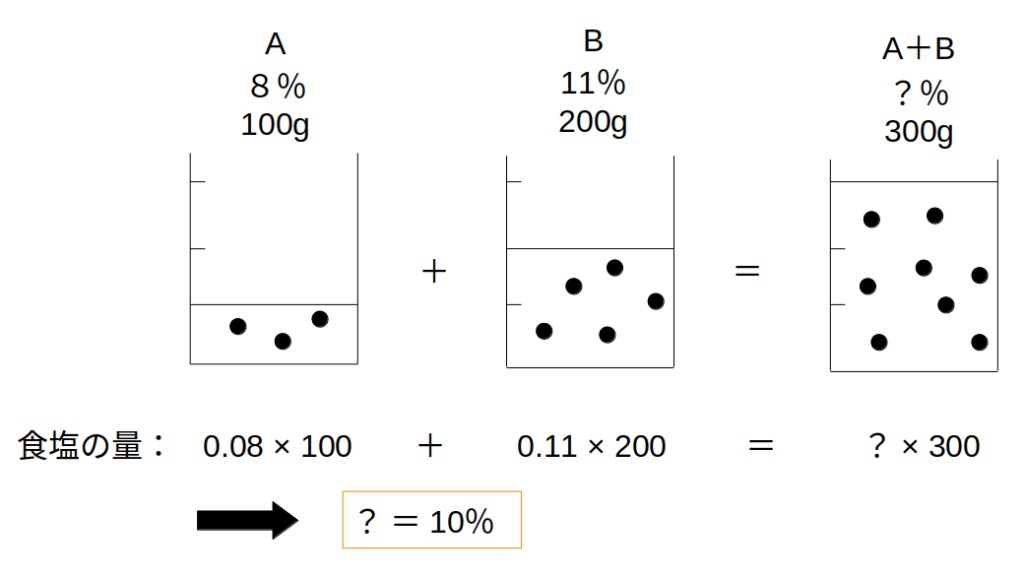
8%の食塩水100g(A)と、11%の食塩水200g(B)を混ぜたときの濃度はいくらか。
【溶けている食塩の量】を書き出します。

「食塩の量=濃度(%)×食塩水の質量(g)」を使う
A:0.08×100
B:0.11×200
→A+B:?×(100+200)
%は割合に直してます。

いまの場合は%のまま計算しても問題ないけどね
食塩の総量は、混ぜる前後で変わらないので、
8×100+11×200=?×300
→?=0.1
→10%(答)
【2】薄める:水を加えるパターン
食塩水と水(or 食塩)を混ぜる場合も、食塩の量に注目して等式を立てます。
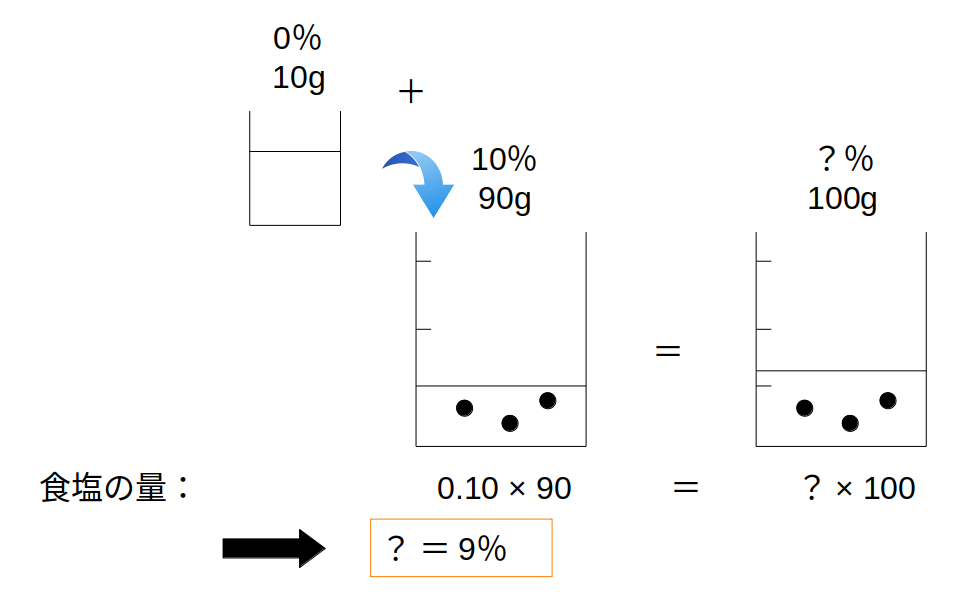
10%の食塩水90gに、10gの水を加えたときの濃度はいくらか。
【溶けている食塩の量】を書き出すと、
薄める前:0.1×90
薄めた後:?×(90+10)

食塩を加えるなら「後:?×(90+10)+10」になる
薄めても食塩の量は変わらないので、
9=?×100
→?=0.09
→9%(答)

カップ麺のスープを飲み干すなら、味が薄くても塩分の摂取量は同じってこと
【3】蒸発:水が減るパターン
蒸発させる場合も、食塩の量がカギ。
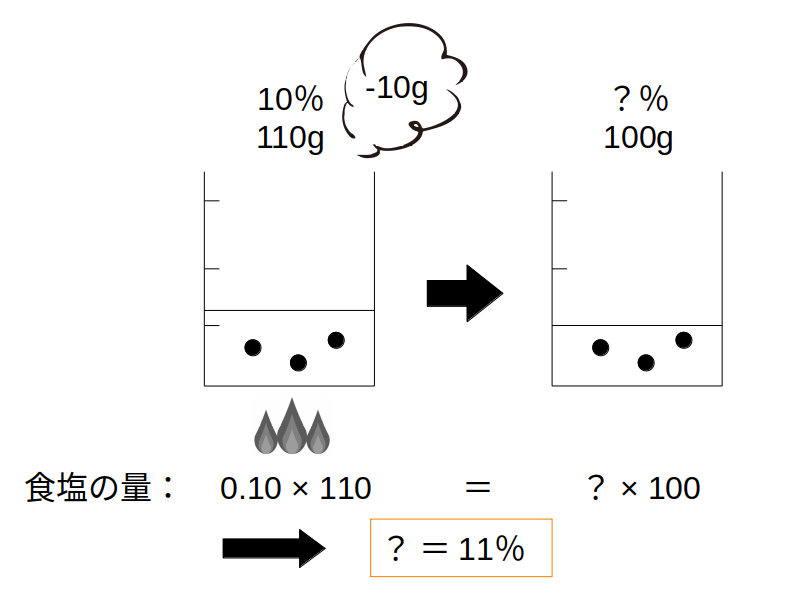
10%の食塩水110gを加熱し、10gの水を蒸発させたときの濃度はいくらか。
やはり、前後の食塩の量を書き出します。
蒸発前:0.1×110
蒸発後:?×(110ー10)
加熱しても食塩は消えないので、【溶けている食塩の量】で等式が立ちます。
11=?×100
→?=0.11
→11%(答)

夕飯の残りの味噌汁ってしょっぱくなりがちよね
結論:「混ぜる・薄める・蒸発」には食塩の量
食塩水の濃度計算を解くカギは、【溶けている食塩の量】。
濃度計算の基本パターン、「混ぜる・薄める・蒸発」のいずれにも有効です。
やや抽象的ですが、濃度の公式だけ知ってればOKなやり方。

直感的な方が分かりやすいならてんびん図もいいよ
応用範囲の広い解き方です。
ほとんどの濃度計算問題に使えるので、ぜひマスターしてください。
以上、食塩水の濃度計算を食塩の量に注目して解く方法の解説でした。
ここからは、数的処理の過去問みたいなオリジナルの演習問題を解きながら、解法の使い方を学んでいきます。
演習問題:濃度計算の応用問題
濃度2%の食塩水が200g入ったビーカーAと、濃度4%の食塩水が100g入ったビーカーBがある。はじめに、Bからある量を取り出してしばらく加熱したところ、質量が10g減少し濃度5%の食塩水となった。これを全てAに加えたあと、水を加えて濃度1.5%の食塩水とした。このとき、加えた水の質量はいくらか。
- 40g
- 80g
- 120g
- 160g
- 200g
4
食塩の濃度計算。
一見複雑そうでも、基本パターンの問題が分かれば解けます。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:食塩の量で等式を立てる
複数の操作が入り混じっています。
これを、「混ぜる・薄める・蒸発」のパターンに分解してみます。
ステップ1:Bからある量を取り出し、10g蒸発させ濃度5%の食塩水とした
ステップ2:ステップ1を全てAに加えた
ステップ3:水を加えて1.5%の食塩水とした

複雑に見えても、実は基本の組み合わせ
問題を解くカギは、やっぱり【溶けている食塩の量】。
ステップごとに、食塩の量に関する等式を立てていきます。
【1】蒸発:濃度は変わっても食塩の量は同じ
加熱の前後において、濃度計算の三要素「食塩水・濃度・食塩」を書き出します。
取り出した食塩水の質量が不明なので、\(b\)gとします。
| 食塩水(g) | 濃度(%) | 食塩(g) | |
| 蒸発前 | \(b\) | 4 | \(b\)×4×0.01 |
| 蒸発後 | \(b\)ー10 | 5 | (\(b\)ー10)×5×0.01 |
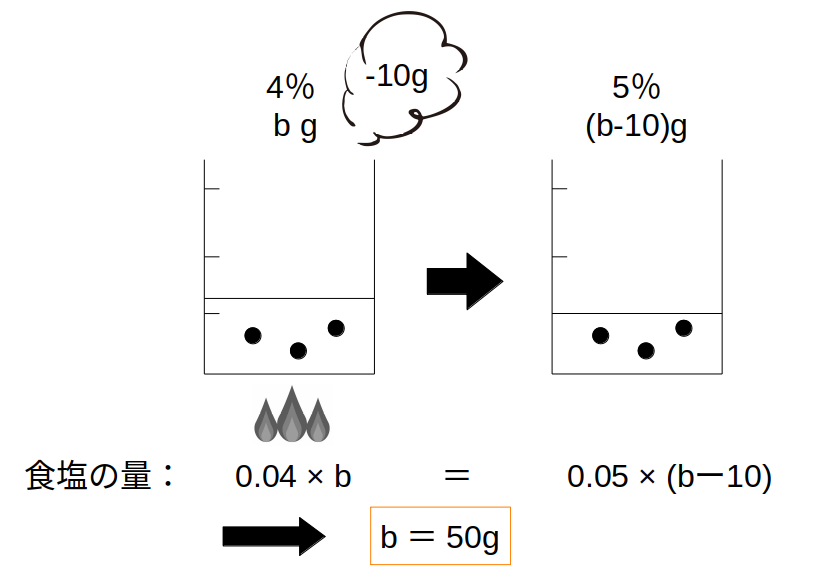
加熱の前後で、含まれる食塩の量はイコールです。
4\(b\)=5(\(b\)−10)
→\(b\)=50g

Bの50g(4%)を加熱して、5%の食塩水40gができた…(B’)
【2】混ぜる:食塩の総量は不変
これも【溶けている食塩の量】を追うことが大切。

混ぜた後の濃度が分からないので、仮に\(c\)としています。
全体で見れば、食塩の総量は混ぜる前後で変化しません。
上の筆算でいう、右端の項がイコールです。

AとB’を混ぜてCなら、食塩量はA+B’=C
200×0.02+40×0.05=240×\(c\)
→\(c\)=0.025
→2.5%
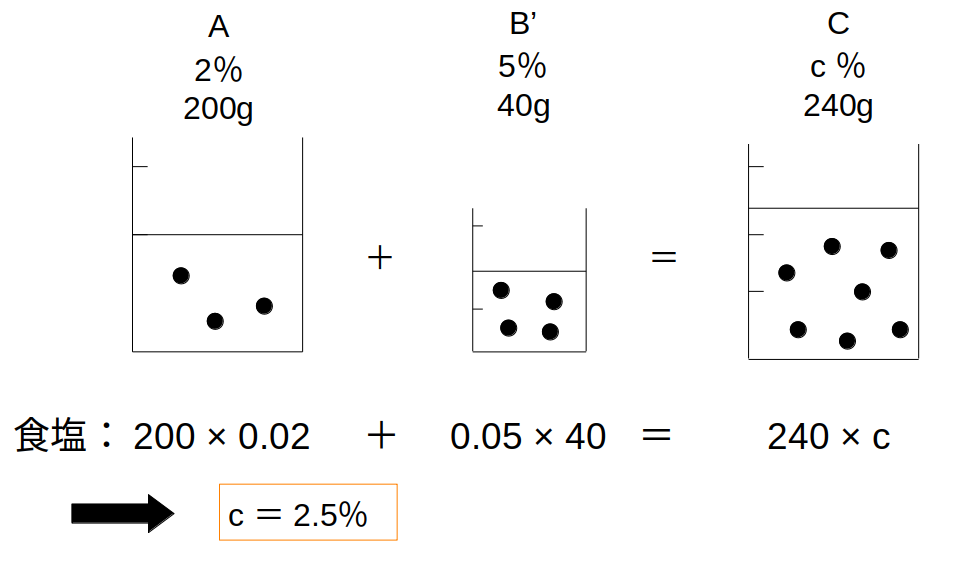

2.5%食塩水が240gできた…(C)
【3】薄める:水を加えても食塩は消えない
今度も【溶けている食塩の量】の関係を式にします。
加えた水の量(求める値)を\(\x)gとします。
| 食塩水(g) | 濃度(%) | 食塩(g) | |
| 前 | 240 | 2.5 | 240×2.5×0.01 |
| 後 | 240+\(x\) | 1.5 | (240+\(x\))×1.5×0.01 |
水を加えても、食塩が増えたり減ったりすることはありません。
やはり、水を加える前後で食塩の量はイコールです。
240×2.5×0.01=(240+\(x\))×1.5×0.01
→\(x\)=160g…(答)
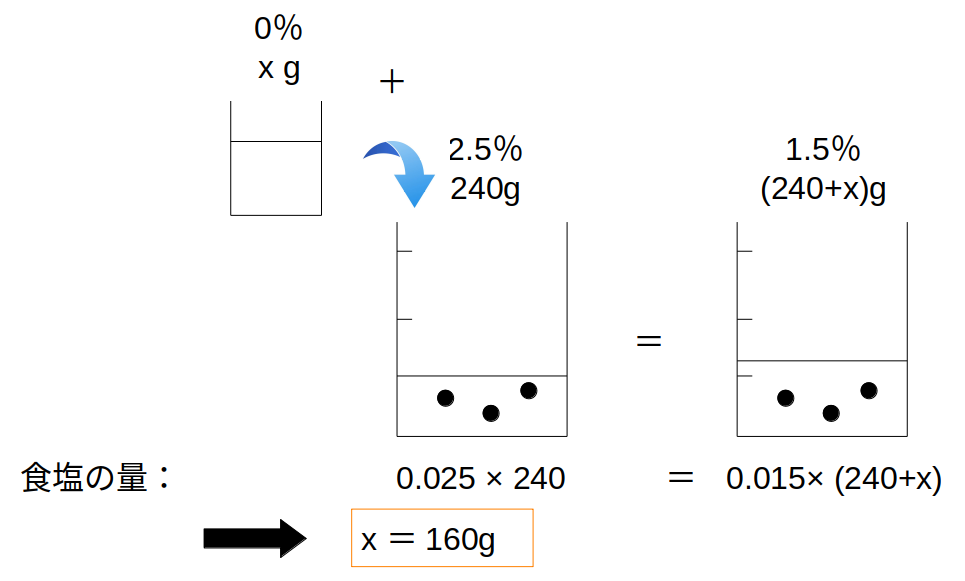

加えた後の食塩水をまるごと\(x\)とおいてもOK
よって、4が正解です。
おわりに:濃度計算は食塩の量で解く
お疲れ様でした!
食塩水の濃度計算は、【溶けている食塩の量】がカギ。
「混ぜる・薄める・蒸発」によって、食塩の総量が変わることはありません。
混ぜる前後の食塩の量を書き出せば、総和はイコールとなります。
今回は、複数の工程を経て1.5%の食塩水を作る問題でした。
まずは「混ぜる・薄める・蒸発」に分解。
個々のステップについて、【溶けている食塩の量】で式を立てて解きます。
もう1問、難しめのやつもどうでしょう?
【緊急】セブンのグミチョコめっちゃ美味いよ

あーあ、明日絶対品薄だわ
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
「Bからある量を取り出してしばらく加熱したところ、10g蒸発し濃度5%の食塩水となった」について。
| 食塩水(g) | 濃度(%) | 食塩(g) | |
| 蒸発前 | \(b\) | 4 | \(b\)×4×0.01 |
| 蒸発後 | \(b\)ー10 | 5 | (\(b\)ー10)×5×0.01 |
蒸発の前後で、溶けている食塩の量は不変なので、
4\(b\)=5(\(b\)−10)
→\(b\)=50g
「これを全てAに加えた」について。

【2】混ぜ合わせる前後の食塩の総量はイコール
溶けている食塩の総量は混ぜる前後で増減しないので、
200×2+40×5=240×\(c\)
→\(c\)=2.5%
「水を加えて1.5%の食塩水とした」について。
| 食塩水(g) | 濃度(%) | 食塩(g) | |
| 前 | 240 | 2.5 | 240×2.5×0.01 |
| 後 | 240+\(x\) | 1.5 | (240+\(x\))×1.5×0.01 |
薄めても溶けている食塩の量は同じなので、
240×2.5×0.01=(240+\(x\))×1.5×0.01
→\(x\)=160g…(答)
よって、4が正解である。





コメント