- 整数の分野でよく出る「倍数・約数・余り」を使った解法が身につく
- 過去問の類題を例に、本番で役立つ「解法のポイント」の使い方を学べる
- どこよりも詳しい解説で、本試験レベルの問題を完全理解
→数的処理の「あと一点」が実現!
こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
今回のテーマは「整数」です。
整数問題で頻出の解法を、前回の記事で紹介しました。
整数問題を諦めたくない方(そうでない方も)、必見です。

整数で悩むあなたに、一筋の光明を
演習問題:誤った情報からカードの数字を当てるゲーム
10〜99の二桁の整数が書かれた90枚のカードがある。いま、Aがこれをシャッフルし、無作為に1枚取り出した。取り出したカードの数字について、AはBに次のようなヒントを与えた。
ヒント:その数の各桁の数字を足し合わせた和は7である。
Bは、Aが引いたカードの数字を当てるため、さらに次のような質問をした。質問に対し、Aは「はい」か「いいえ」のいずれかが書かれた札を見せることで回答した。
質問I:その数は50より大きいか?
質問II:その数は偶数か?
ところがこの質問に回答したAは、「はい」と「いいえ」の札を取り違えており、2つの質問の回答がいずれも誤りであったことが後に分かった。この誤った2つの回答と「ヒント」をもとに、Bがカードの数字を推測したところ、候補は複数あった。そこで、候補を絞るため、Bは追加で次のような質問をした。
質問III:ある整数を二乗した数に8を加えた数は、その数より小さいか?
このとき、Aが引いたカードの数字は次のうちどれか。
- 34
- 43
- 52
- 61
- 70
4
二桁の整数を当てる問題です。
基本に忠実に、「解法のポイント」が有効です。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それでは、解説スタート!
解説:候補が挙がればしらみつぶしが可能
「解法のポイント」に沿って解いていきます。
- 範囲を絞る
- 倍数、約数、余りから候補を書き出す
- しらみつぶしで特定
引いたカードに書かれた整数の範囲は?
ズバリ「10〜99の二桁の整数」が範囲です。
Aが引いたカードの数字を\(n\)とすれば、\(10≦n≦99\)
候補は「各桁の数字の和が7となる二桁の整数」
範囲を絞ったら、候補となる整数をピックアップします。
候補を選び出すための基準は、「ヒント」に与えられています。
つまり、「各桁の数字の和が7となる二桁の整数」を書き出せばOKです。
以下の整数が候補です。
16,25,34,43,52,61,70

桁の和が7となる整数は、○と|の並びで考えよう
以下は25と34の例。
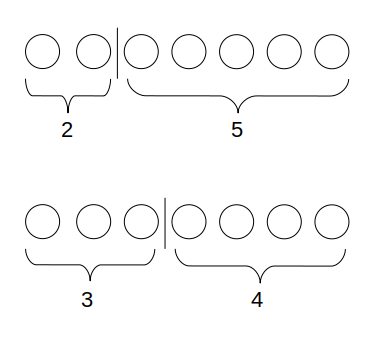
推測の結果を書き出してしらみつぶし
候補をピックアップしたら、あとはしらみつぶしです。
3つの質問から、引いたカードの数字を推測します。
まず「誤った2つの回答と『ヒント』をもとに、Bがカードの数字を推測したところ、候補は複数あった」について。
2つの質問それぞれに「はい」「いいえ」がありますが、この程度なら全パターンを書き出してしまった方が分かりやすいです。
質問への回答に対し、推測の結果を書き出します。
以下の表では、「はい」をY、「いいえ」をNと表しています。
| \(n>50\) | 偶数 | |||
| (i) | Y | Y | 52 | 70 |
| (ii) | Y | N | 61 | |
| (iii) | N | Y | 16 | 34 |
| (iv) | N | N | 25 | 43 |
ここに質問IIIを加味します。
7つある数字の候補16,25,34,43,52,61,70
のうち、質問IIIに該当するのは34と61だけです。
したがって、Bが考えていたパターンは(iii)のNYであったことが分かります。

(ii)だと「候補は複数あった」という前提に反するからね
Aは誤った回答をしていたので、正しくはその反対、(ii)のYNになります。
これより、Aが引いたカードの数字は61に決まります。
以上より、4が正解です。
おわりに:整数は範囲が決まれば書き出してしらみつぶしできる
お疲れ様でした!
整数問題でまず大切なのは、範囲を決めること。
範囲さえ決まれば、書き出してしらみつぶしが可能です。
今回は、3つの質問から2桁の整数を特定する問題でした。
質問の答えに誤りが含まれるところがややこしいですが、「解法のポイント」に沿って解くことができます。
範囲を絞って書き出してしらみつぶし、という基本の流れをマスターしてください。
「解法のポイント」を確実に身につけるため、次の問題にもチャレンジしてみてください。
卵の殻は意外と割れない
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
Aが引いたカードの数字を\(n\)とすれば、\(n\)は二桁の整数だから
\(10≦n≦99\)
このうち、「各桁の数字の和が7となる二桁の整数」は以下の7つ。
16,25,34,43,52,61,70
質問IおよびIIに対し、「はい」「いいえ」の全回答パターンと該当する整数を書き出すと、次のようになる。
| \(n>50\) | 偶数 | |||
| (i) | Y | Y | 52 | 70 |
| (ii) | Y | N | 61 | |
| (iii) | N | Y | 16 | 34 |
| (iv) | N | N | 25 | 43 |
このうち、質問IIIに該当するのは34と61だけなので、Bが推測した整数は(iii)の16と34である。
Aの回答が誤りであったことより、正しくは反対の(ii)の61である。
よって、4が正解である。

コメント