こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「集合の要素数」
数的処理で何かと目にするこの単元。
今回は、特に「キャロル表」に焦点を当ててみたいと思います。
キャロル表は、「……かつ〜」とか「○○または××」を満たす集合の要素数(人数)を数えるときに使うものです。
ベン図と並んでよく登場しますが、
「どう使い分けたらいいの?」
という疑問をもつ方が非常に多いようです。

またもソースはヤフー知恵袋
ざっくりお答えすると、
「2集合ならベン図、3集合ならキャロル表」
です。
今回は、集合の要素数の問題で役立つ「キャロル表」について、ベン図との使い分けをていねいに解説します。
後半では、数的処理の過去問に似せた演習問題を解きながら、その使い方を学びます。
講義:キャロル表とベン図の使い分け
もう一度言います。
集合の要素数(人数)を数える問題は、
「2集合ならベン図、3集合ならキャロル表」
です。
もう少し言うと、キャロル表は二者択一の集合3つからなる問題に有効です。
具体的には、「ある/ない」とか「高い/低い」とか「以上/未満」とか……

2集合ならベン図で事足りる
- 2集合→ベン図
- 二者択一(YES/NO)の3集合→キャロル表
簡単な例を挙げて考えてみます。
例題:3集合ならベン図よりもキャロル表
次のことが分かっているとき、うさぎだけを飼っているのは何人か。
- 犬を飼っている人は11人、猫を飼っている人は13人、うさぎを飼っている人は8人
- 犬と猫を飼っている人は7人、猫とうさぎを飼っている人は6人、うさぎと犬を飼っている人は4人
- 犬と猫とうさぎを飼っている人は2人
犬/猫/うさぎの、飼っている/いない……
二者択一の3集合にまつわる問題。

まさにキャロル表の使いどころ
まず、与えられた数値を図のA〜Gに書き込んでいきます。
- 犬→11人
- 猫→13人
- うさぎ→8人
- 犬&猫→7人
- 猫&うさぎ→6人
- うさぎ&犬→4人
- 犬&猫&うさぎ→2人
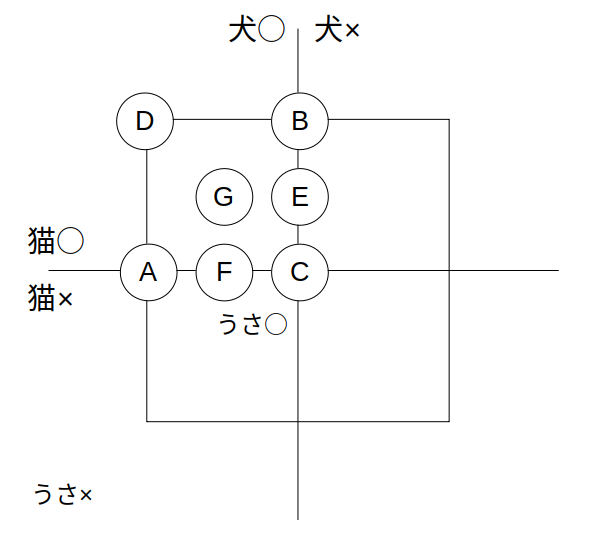
書き込んだ図は次の通り。
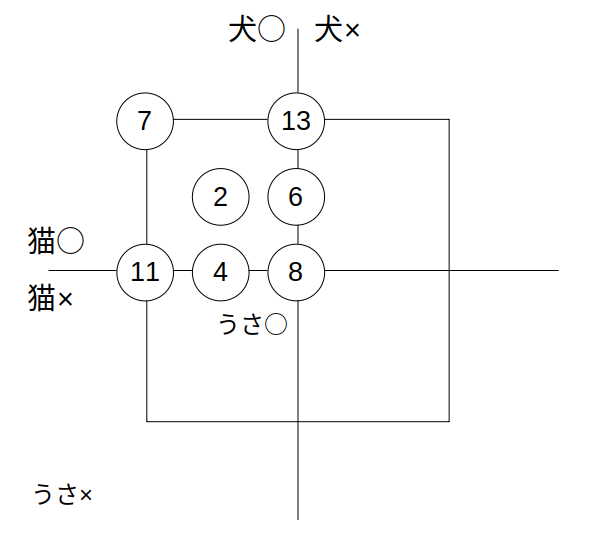
求めるものは、うさぎ「だけ」を飼っている人数。
なので、右下の四角形の内側を\(x\)とします。
ほか、\(x\)を求める過程で使う数値も文字でおきます。
\(x\)や、すでに分かっている数値と隣り合う場所は必要となる可能性が高いです。

文字を使わないで、計算できる場所を埋めていってもOK
ここでは、「6」の右隣を\(a\)、\(a\)と\(x\)の間を\(b\)とおきます。
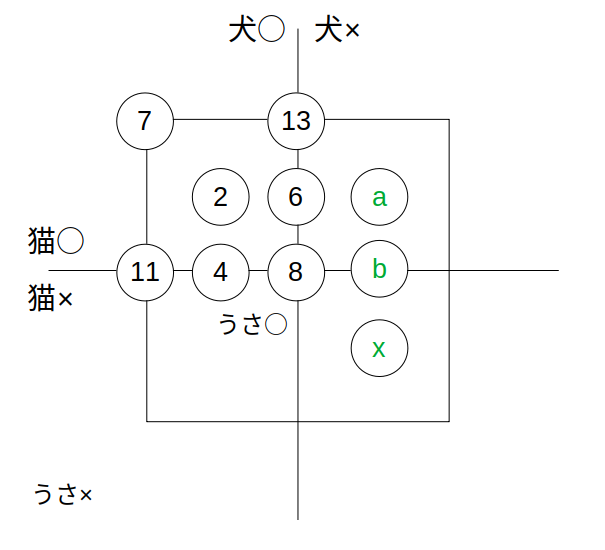
四角形の上半分で、
\(2+a=6\)
→\(a=4\)
四角形の内側の横軸上で、
\(4+b=8\)
→\(b=4\)
よって、\(a+x=b\)
→\(x=0\)人(答)
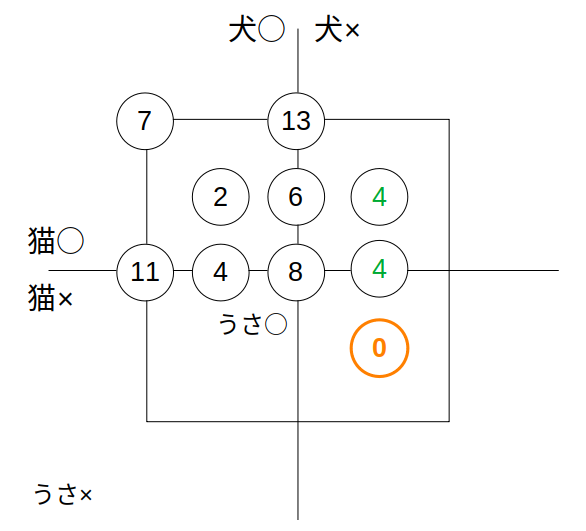

うさまるってキャラクターいるよね
ベン図で解くと……
ベン図を使った解き方では、区切られた領域の人数を文字でおくのが定石。
ベン図を描いて、求める人数を\(x\)、それ以外の領域を\(a,b\)とおきます。
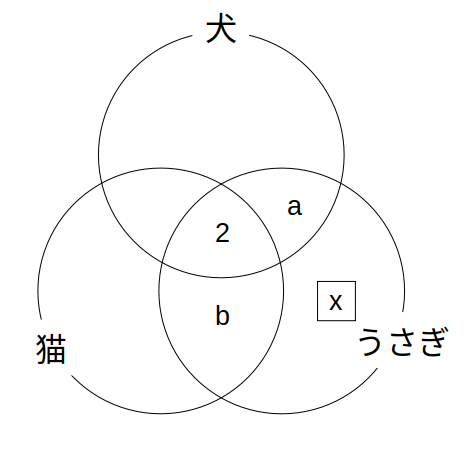
2集合の円の重なり(共通部分)に注目すると、
猫&うさぎ:\(b+2=6\) → \(b=4\)
うさぎ&犬:\(a+2=4\) → \(a=2\)
うさぎの円に注目すると、
\(x+a+b+2(=x+2+4+2)=8\) → \(x=0\)人(答)
キャロル表のメリット
こう見ると、キャロル表で解くのもベン図で解くのも同じに思えます。
しかし、実際の試験で使うなら、前者の方が有利です。
試験では、図を手書きしなければならないことを思い出してください。
まず、3集合のベン図ってちょっと書きにくい。
試験は時間勝負ですから、そう何度も書き直せません。
かといって見づらいまま考えると、計算ミスや思い違いを生むリスクが高まります。

重なりの領域が小さすぎて数値を書けない、とかありがち
もう一つ、領域をまたいだ数値を書き表しにくいのもベン図の欠点です。
上の例題なら、「猫&うさぎ」とか「うさぎ&犬」の数値をどこに書いていいか、という問題があります。

無理くり重ねて書くと見づらいしねぇ
この点、キャロル表は四角形と十字線だけで難なく書けます。
しかも、個々に書き込む場所が用意されているので、数値や文字を全て図に落とし込んでしまえるのも強みです。

デメリットは足し引きの関係がぱっと見で分かりにくいことかな
結論:3集合ならキャロル表
このように、3集合の要素数に関する問題を考えるのに、ベン図は最適とはいえません。
慣れは必要ですが、二者択一の3集合ならキャロル表で解くのがオススメです。
そんなわけで、要素数の問題は「2集合ならベン図、3集合ならキャロル表」です。

ベン・キャロルって映画俳優にいそう
以上、ベン図とキャロル表の使い分け方の解説でした。
ここからは、過去問をもとに作ったオリジナルの演習問題を解きながら、「解法のポイント」の使い方を学んでいきます。
演習問題:生徒を対象としたアンケート結果の集計
ある学校で、生徒を対象にテストの成績と学外の生活に関する調査を行った。結果について、次のことが分かっているとき、確実に正しいといえるのはどれか。
- 5科目の平均が50点以上の者は83人、50点未満の者は67人である。
- 朝食を食べる習慣がない者は61人である。
- 朝食を食べる習慣があり、習い事をしておらず、5科目の平均が50点未満の者は22人である。
- 朝食を食べる習慣がなく、5科目の平均が50点未満の者のうち、習い事をしている者は、そうでない者より5人多い。
- 習い事をしておらず、5科目の平均が50点未満の者は30人である。
- 習い事をしており、5科目の平均が50点以上の者のうち、朝食を食べる習慣がある者は17人であり、そうでない者より5人少ない。
- 習い事をしている者は75人である。
- 5科目の平均が50点以上で、朝食を食べる習慣があり、習い事をしていない者は28人である。
- 5科目の平均が50点未満で、朝食を食べる習慣があり、習い事をしている者は21人である。
- 5科目の平均が50点以上の者のうち、朝食を食べる習慣がある者は、そうでない者より多い。
- 朝食を食べる習慣がない者のうち、習い事をしている者は、そうでない者より少ない。
4
アンケート調査の回答結果を集計する問題。
個々の質問を集合と見なせば、同じ回答をした人数が要素数です。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:二者択一の3集合にはキャロル表
条件を見るに、質問項目は3つで、回答は「YES/NO」式の二者択一。
- 5科目の平均が50点以上/未満
- 朝食を食べる習慣がある/ない
- 習い事をしている/いない
二者択一で3集合なら、キャロル表が有効です。
- 2集合→ベン図
- 二者択一(YES/NO)の3集合→キャロル表
次のようなキャロル表を用意し、人数を書き込んでいきます。
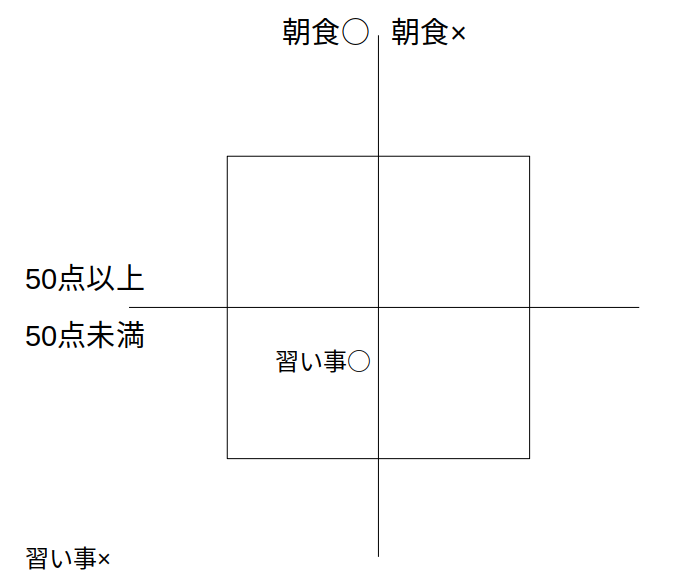
分かっている数値をキャロル表に書き込む
まずは数値を書けるところから記入します。
1つ目の条件5科目の平均が50点以上の者は83人、50点未満の者は67人である。
→橙
2つ目の条件朝食を食べる習慣がない者は61人である。
→青
3つ目の条件朝食を食べる習慣があり、習い事をしておらず、5科目の平均が50点未満の者は22人である。
→緑
5つ目の条件習い事をしておらず、5科目の平均が50点未満の者は30人である。
→黄
6つ目の条件習い事をしており、5科目の平均が50点以上の者のうち、朝食を食べる習慣がある者は17人であり、そうでない者より5人少ない。
→紫
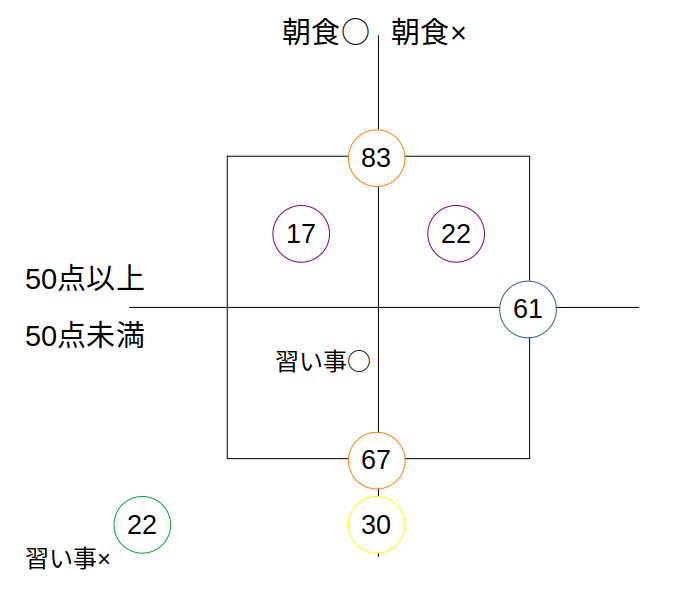
1つ目の条件5科目の平均が50点以上の者は83人、50点未満の者は67人である。
に注目すると、回答者は全部で83+67=150人
これより、朝食を食べる習慣がある者は150ー61=89人
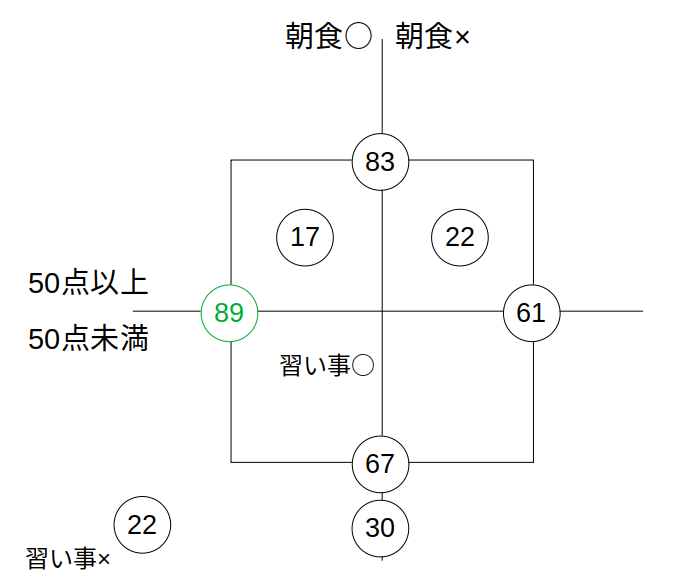
選択肢からゴールを決める
書き込んだ数値をもとに、キャロル表を埋めていきます。
手当り次第に記入するという手もありますが……
先にゴールを見定めて、そこに向かっていく方が合理的。
選択肢に関係のある数値の場所(一〜五)をあらかじめマークします。
ここを埋めるのが本問の最終目的です。
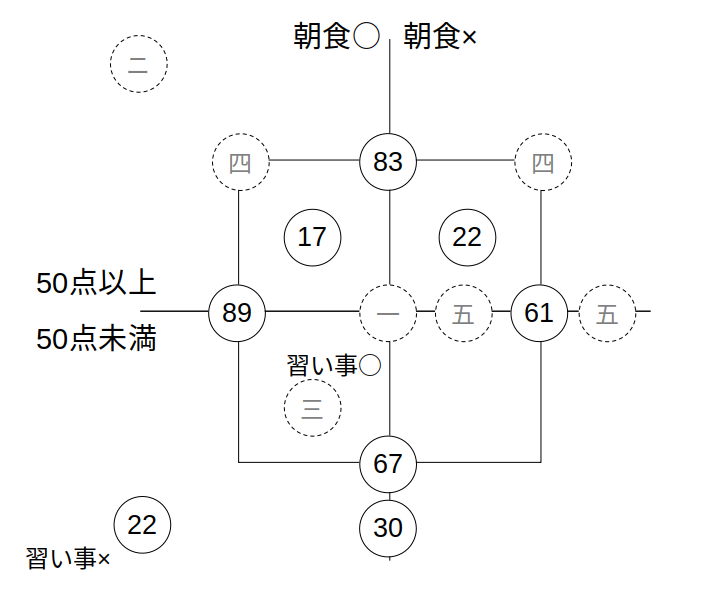
「端+端=真ん中」でキャロル表を埋める
まず、図の一番下、横に並んだ数値に注目。
「端+端=真ん中」の関係を使うと、右下(四角形の外側)が分かります。
つまり、22+?=30より、?=30ー22=8人
すると、
4つ目の条件朝食を食べる習慣がなく、5科目の平均が50点未満の者のうち、習い事をしている者は、そうでない者より5人多い。
が使えます。
四角形の内側の右下は、8+5=13人
これより、四角形の右下の頂点は、8+13=21人

ここも「端+端=真ん中」
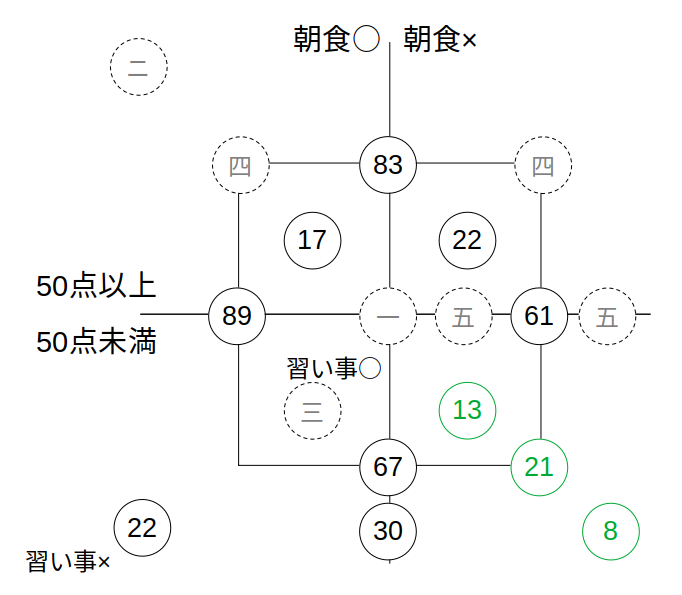
続いて、四角形の右の辺(四右、61、21)の並びに注目します。
「端+端=真ん中」と使うと、四右=61ー21=40人
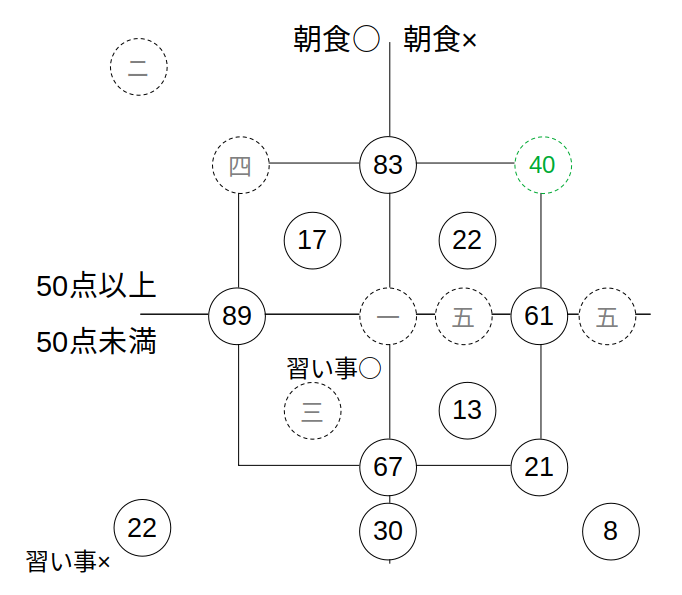

ん?もう一個の四も分かるんじゃね?
その通り!
よく気が付きましたね!
気づかせた筆者もスゴイ!

隙有自画自賛
今度は四角形の上の辺(四左、83、40)の並びに注目。
同じく「端+端=真ん中」を使って、四左=83ー40=43人
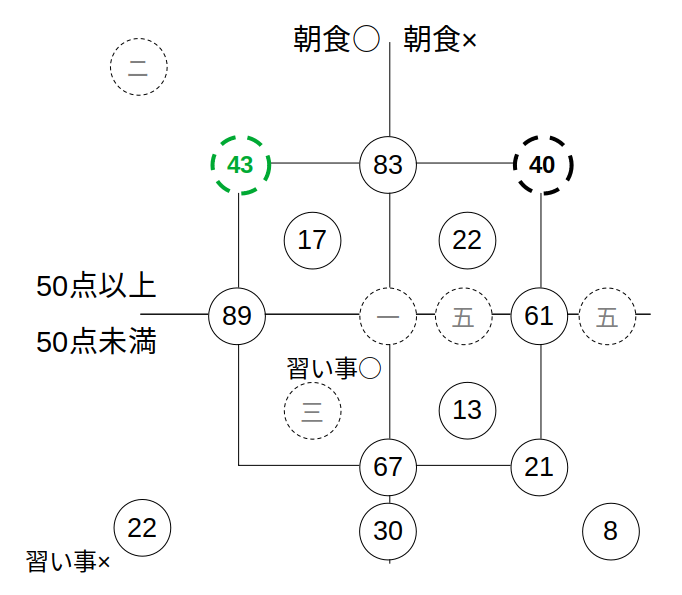
これより、平均50点以上の人について、「朝食○>朝食×」
つまり、選択肢4は正しいことになります。
よって、4が正解です。
ちなみに……
一〜五は全て埋めることができます。(次図)
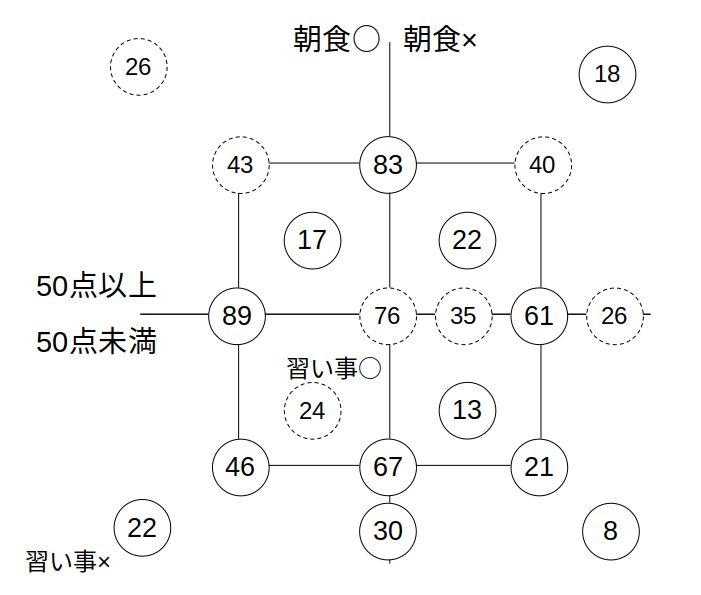
おわりに:2集合はベン図、3集合はキャロル表
お疲れ様でした!
集合の人数(要素数)の問題は、集合がいくつあるかによって対処法が変わります。
2集合ならベン図、3集合ならキャロル表です。
キャロル表に数値を書き込んだら、芋づる式に分かるところを埋めていきます。
コツは、3つ並んだ数を見つけて「端+端=真ん中」の関係を使うこと。
今回は、3つのアンケート項目の回答を、キャロル表を使って集計する問題でした。
キャロル表は初めは取っつきにくいですが、覚えてしまえば機械的に解くことができます。
さまざまな問題を解いて、使い方に慣れてください。
過去にも似た系統の問題を解説しています。
国家総合職ですが。
ソシャゲでハロウィンイベント来ると今年も終わりかーってなる

年を追うごとに1年が短くなるよ
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
次のようなキャロル表を用意する。

本問のキャロル表
1つ目の条件「5科目の平均が50点以上の者は83人、50点未満の者は67人である。」
→橙
2つ目の条件「朝食を食べる習慣がない者は61人である。」
→青
3つ目の条件「朝食を食べる習慣があり、習い事をしておらず、5科目の平均が50点未満の者は22人である。」
→緑
5つ目の条件「習い事をしておらず、5科目の平均が50点未満の者は30人である。」
→黄
6つ目の条件「習い事をしており、5科目の平均が50点以上の者のうち、朝食を食べる習慣がある者は17人であり、そうでない者より5人少ない。」
→紫
1つ目の条件に注目すると、回答者は全部で83+67=150人
これより、朝食を食べる習慣がある者は150ー61=89人

全体の人数が分かる
次図に、選択肢に関係のある数値の場所(一〜五)を示す。

選択肢に関係する場所一〜五
先に書き込んだキャロル表をもとに一〜五を求めると、次のようになる。

一〜五が全て埋まる
これより、選択肢4が正しい。
よって、4が正解である。




コメント