こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「平面図形」
数的処理では毎年のように出題される重要な単元。
今回は、特に「回転する図形の軌跡」を扱います。
このテーマでありがちなのが、
「回転移動や軌跡がイメージできない」
という悩み。
図を書くこともままならず、苦手意識を持ってしまう方も多いでしょう。

やっぱりソースはヤフー知恵袋
筆者もお絵描きは苦手で、図を書いて考える問題には苦戦してました。
しかし、軌跡の問題は美術のテストではありません。
イメージできないのはセンスの問題ではなく、意識すべきポイントを分かっていないからなんです。
要点さえきちんと押さえていれば、軌跡のおおまかな形はイメージできます。

少なくとも問題は解けるように作られてる
そんな、軌跡の問題を解くために「意識すべきポイント」とは?
今回は、平面図形の「軌跡」を解くためのポイントについて、ていねいに解説します。
後半では、数的処理の過去問に似せた演習問題を解きながら、その使い方を学びます。
講義:回転する図形の軌跡をイメージするコツ
図形の回転移動の軌跡で意識したい3つのポイントを伝授します。
- 小さなステップに分ける
- 回転の中心、半径、回転角を押さえる
- 繰り返し(対称性)にも注意
小さなステップに分ける
いきなり全体を捉えようとするのはムズカシイ。
まず小さなステップに分けると、軌跡が単純化されイメージしやすくなります。
回転移動の中に、状況が変化するタイミングがいくつかあります。
そこから次の変化点までの間を1ステップとして、回転移動を細切れにします。
各ステップの軌跡は円弧なので、イメージしやすいはず。

円弧をつなげたものが軌跡の全体像になる
多角形の場合、辺が地面に着いたときが変化点です。
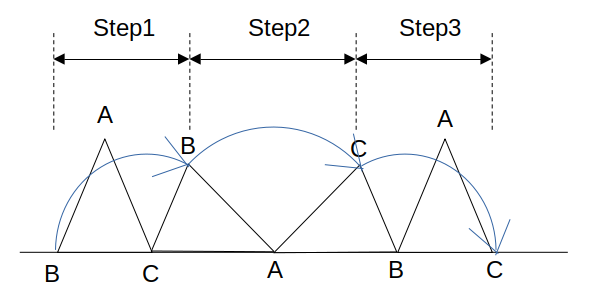
例えば三角形の頂点の軌跡なら、次図のような3ステップに分割できます。
すると、各ブロックは円弧の形で、軌跡はこれがつながったものだな、と理解できます。
回転の中心、半径、回転角を押さえる
回転移動の軌跡をイメージする上で重要な要素が、回転の中心と半径、回転角の3つ。
なぜ重要かというと、この3つこそ、円弧を形作るのに必要な要素だからです。

これらが決まると、円弧の形が決まる
分割した各ブロックのそれぞれで、「どこを中心に、どの半径がどれくらい回転するのか」を意識します。
繰り返し(対称性)にも注意
図形の回転移動は、何らかの周期性を含んでいる場合が多々あります。
繰り返しの動きは一回分だけを考えれば済むので、ここに気づくと手順を少なくできます。
圧倒的に手数が減ってお得です。

利用しない手はないね
例題:正方形の内側を転がる三角形の頂点の軌跡
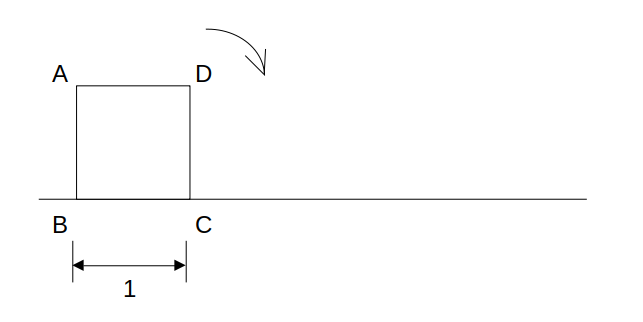
図のように置かれた正方形ABCD(1辺の長さ1)が、水平な地面の上を矢印の方向に滑ることなく2回転するとき、頂点Aの軌跡を描け。
軌跡を小さなステップに分割
先に述べた通り、正方形の各辺が地面に着いたときが変化点です。
最初の1周について、地面に接する1辺がBC→CD→DA→AB→BCと変わる4つのステップに分けて考えます。
回転の中心、半径、回転角を確認
各ステップで、回転の中心&半径&回転角は下表の通り。
| 中心 | 半径 | 回転角 | |
| BC→CD | C | CA | 90° |
| CD→DA | D | DA | 90° |
| DA→AB | A | A(点) | 90° |
| AB→BC | B | BA | 90° |
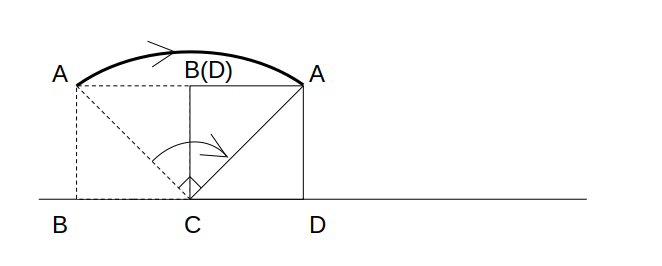
ピンとこない方のために、例として、BC→CDの回転移動を考えます。
まずは回転の中心。
時計方向に回るので、B側が浮き上がってCが回転の中心となります。
次は半径。
頂点Aが中心Cの周りを回るので、半径はCA。
あとは回転角。
正方形の外角の分だけ回るので、頂点AもCの周りを90°回転します。
以上より、この区間の軌跡は「半径\(\sqrt{2}\)、中心角90°の円弧」になると分かります。
イメージしづらい方は、回転の動きをコマ撮りしてみましょう。
中間の状況を2つくらい書き足すと、大分イメージしやすくなります。
4コママンガみたいに。
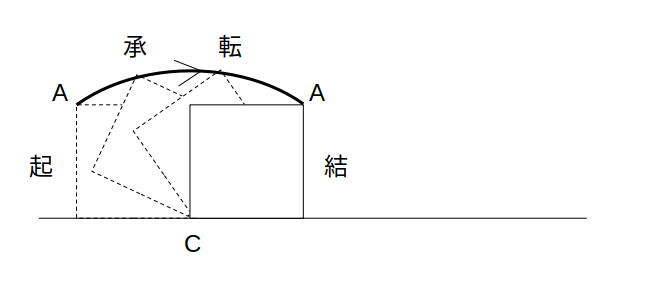

この場合、どちらかというと「転転転転」
同じように考えていくと、1回転の軌跡が描けます。
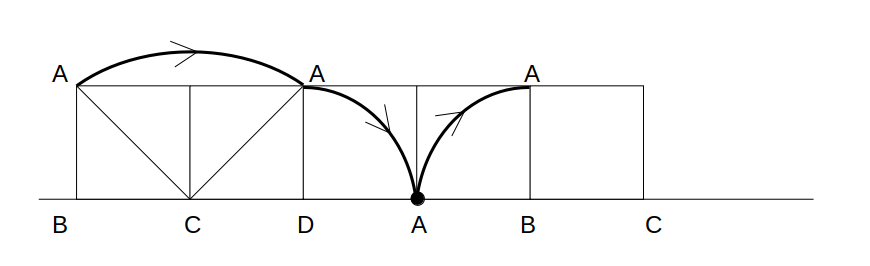
繰り返し(対称性)にも注意
この場合、2回転目は1回転目の繰り返し。
よって、2回転目の軌跡は全く同じ形になります。
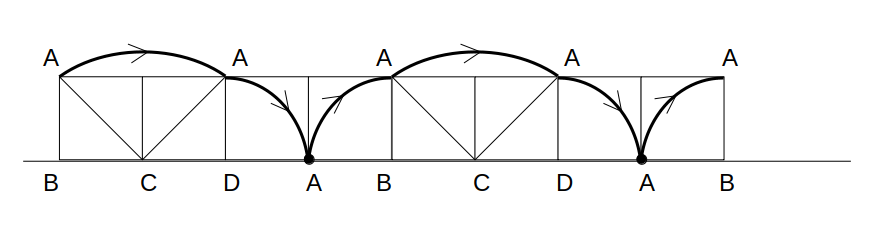
結論:回転する図形の軌跡は円弧の集まり
回転する図形上の点の軌跡は、円弧に分割できます。
その円弧を決める要素は、中心と半径と回転角、の3つ。
あとは対称性も考慮すれば、最短で軌跡を描けます。
これが、回転する図形上の点の軌跡をイメージするために意識したい3つのポイントです。

前2つは必須。対称性は最悪分からなくても描ける
以上、回転する図形の軌跡をイメージする方法の解説でした。
ここからは、過去問をもとに作ったオリジナルの演習問題を解きながら、「解法のポイント」の使い方を学んでいきます。
演習問題:正六角形の内部を転がる正三角形と軌跡
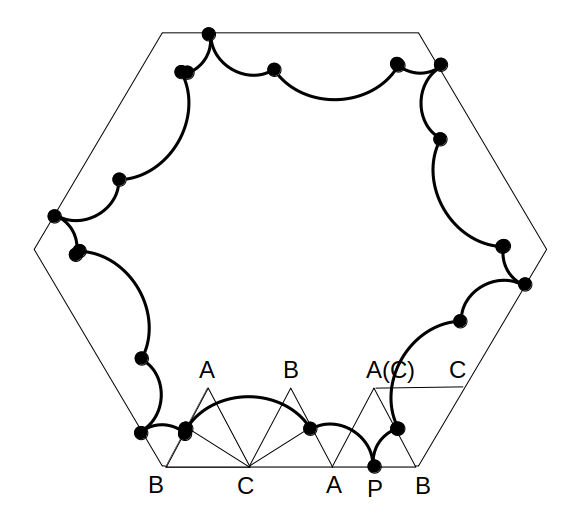
図のように、1辺の長さが6である正六角形の内側に、1辺の長さが2である正三角形ABCがある。いま、△ABCが矢印の方向に滑ることなく回転し、正六角形の内部を辺に沿ってちょうど1周するとき、辺ABの中点Pが描く軌跡の長さはいくらか。
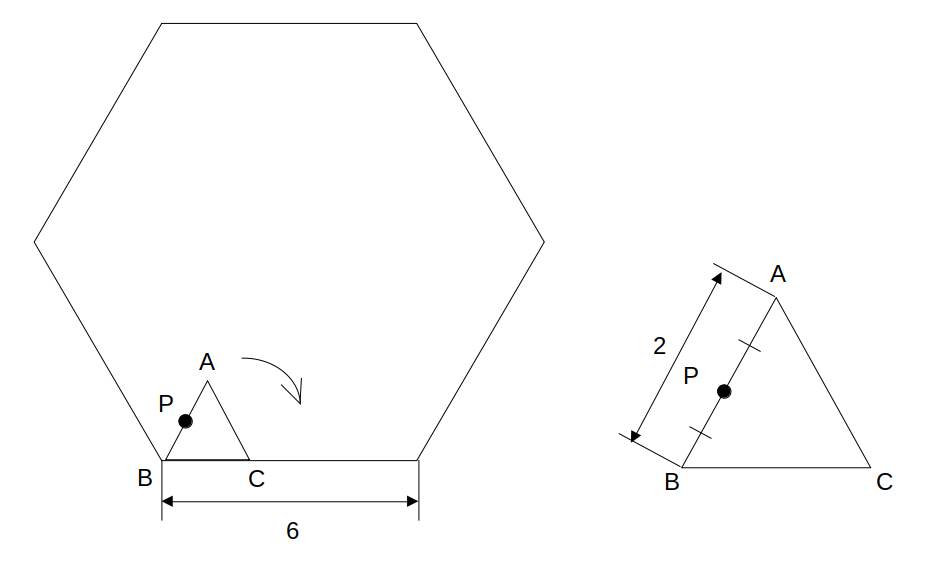
- \(2(1+\sqrt{3})\pi\)
- \(2(1+2\sqrt{3})\pi\)
- \(2(2+\sqrt{3})\pi\)
- \(2(1+2\sqrt{3})\pi\)
- \(2(3+2\sqrt{3})\pi\)
5
正三角形の辺上にある中点の軌跡の問題。
最短で正解を得るために、注目すべきポイントは?
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:分割して中心&半径&回転角。対称性も
「解法のポイント」の3つを意識しつつ進めます。
- 小さなステップに分ける
- 回転の中心、半径、回転角を押さえる
- 繰り返し(対称性)にも注意
軌跡を小ステップに分割
全体を眺めて、キリのいいところで区切ります。
簡単のため、とりあえず正六角形の最初の辺上にいる場合に限って考えます。
すると、各辺が地面に着くときで区切ることができます。
このとき、△ABCは接する辺が「BC→CA→AB」と変化する2ステップを経て端に達します。

正六角形の辺の長さは正三角形のそれの3倍
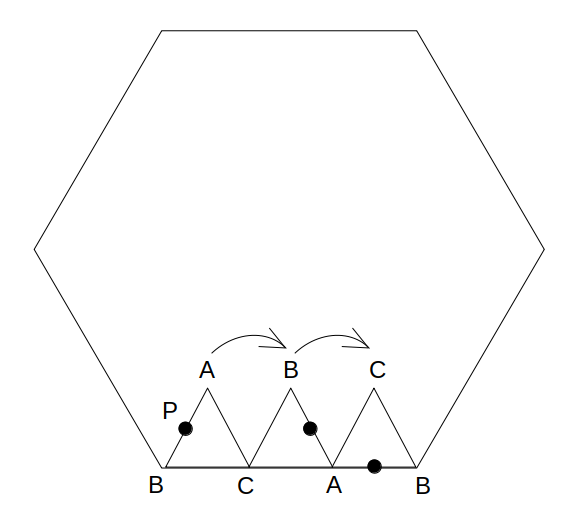
この後、もう1ステップあります。
それは、正三角形ABCがちょっと回転して辺BCが正六角形の次の辺に接する、というステップ。
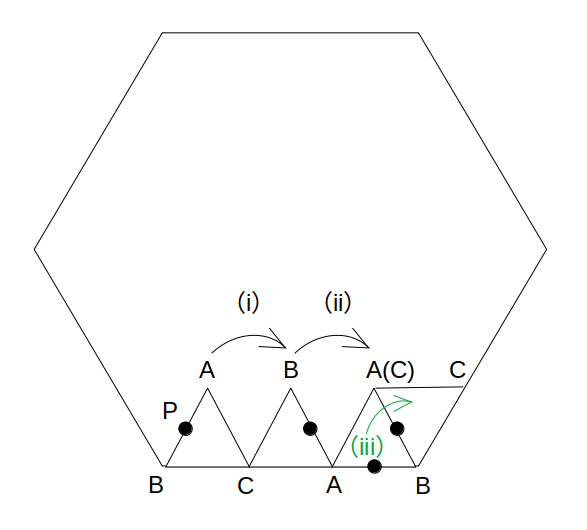
以下、これら3ステップの軌跡の長さを考えます。
回転の中心、半径、回転角を押さえる
3ステップについて、回転の中心&半径&回転角を押さえて軌跡(=円弧)をイメージします。
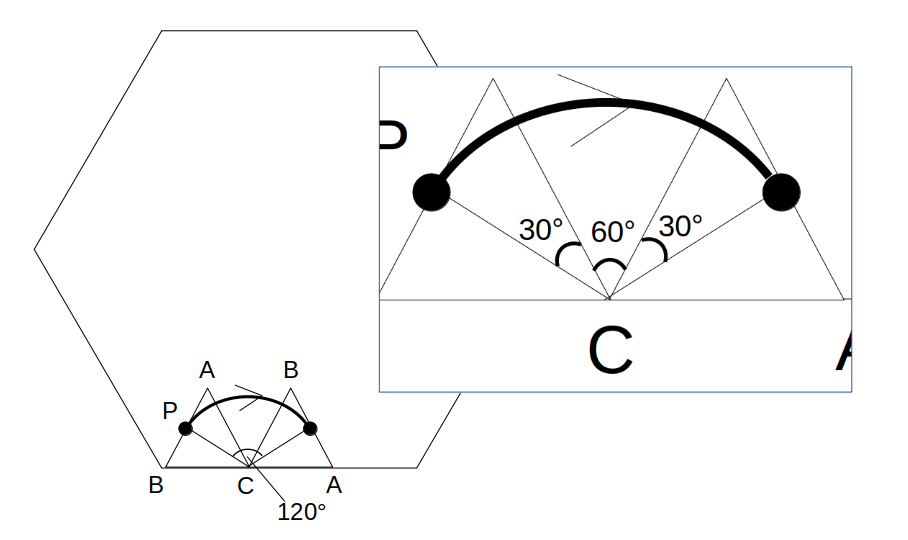
(i)BC→CAの回転の軌跡
中心…頂点C
半径…CP=\(\sqrt{3}\)
回転角…120°(=正三角形の外角)

△ACPは\(1:2:\sqrt{3}\)の三角定規
よって、軌跡は
\[
2\pi × \sqrt{3}×\frac{120}{360}=\frac{2\sqrt{3}}{3}\pi
\]
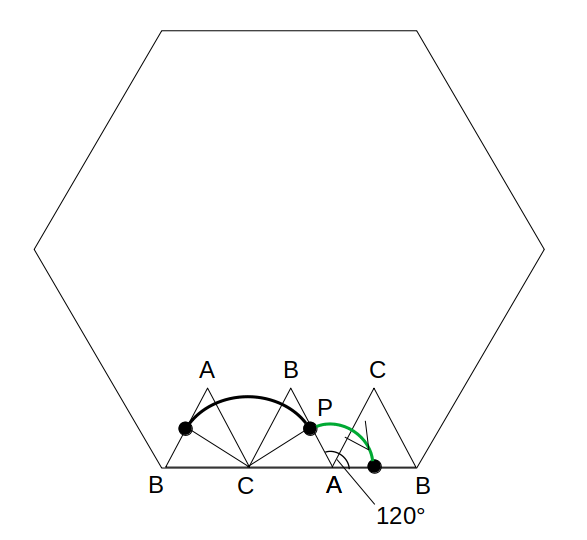
(ii)CA→ABの回転の軌跡
中心…頂点A
半径…AP=1
回転角…120°
よって、軌跡は
\[
2\pi × 1×\frac{120}{360}=\frac{2}{3}\pi
\]
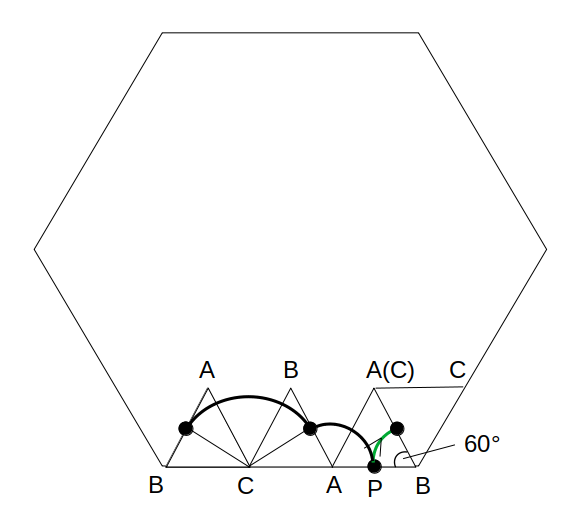
(iii)AB→BC(正六角形の次の辺へ)
中心…頂点B
半径…BP=1
回転角…60°(=正六角形の内角ー正三角形の内角)
これより、軌跡は
\[
2\pi × 1×\frac{60}{360}=\frac{\pi}{3}
\]
(i)、(ii)、(iii)より、軌跡は
\[
\frac{2\sqrt{3}}{3}\pi+\frac{2}{3}\pi+\frac{\pi}{3}=(1+\frac{2\sqrt{3}}{3})\pi
\]
繰り返し(対称性)で軌跡の全体が分かる
(iii)で、△ABCは最初と同じ状況に戻っています。
よって、正六角形の辺の数だけ、(i)〜(iii)の軌跡が繰り返し描かれることになります。
つまり、ここまでの軌跡の長さを6倍したものが全体の長さです。
\[
(1+\frac{2\sqrt{3}}{3})\pi×6=2(3+2\sqrt{3})\pi
\]
よって、5が正解です。
おわりに:軌跡は「分割→中心&半径&回転角→対称性」
お疲れ様でした!
回転する図形上の点の軌跡をイメージするために、意識することは3つ。
【1】小さく分割
【2】中心&半径&回転角
【3】対称性
複雑に思える軌跡も、細切れにすれば円弧です。
その円弧を決める要素は、中心と半径と回転角。
あとは繰り返しに気づけば、最短で軌跡を描けます。
今回は、正三角形の辺の中点が、正六角形の内部を転がってできる軌跡の問題でした。
正三角形の1回転が、ちょうど端から端への移動に相当します。
ここに気づけば、正六角形の各辺で軌跡は同じ形になるだろうと予想できます。
図形の移動はイメージが大切。
向き不向きはありますが、ポイントを押さえれば十分に対処可能です。
回転移動の軌跡には、今回紹介した「解法のポイント」を使ってみてください。
☆もしも「正四面体」だったら
大山のぶ代さん、安らかに。

割とドラえもんの世代だったから訃報聞いて驚いた
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
△ABCがどの辺で接するかによって場合分けする。
(i)BC→CA
中心…頂点C
半径…CP=\(\sqrt{3}\)
回転角…120°(=正三角形の外角)
よって、軌跡は\(2\pi × \sqrt{3}×\frac{120}{360}=\frac{2\sqrt{3}}{3}\pi\)

1ステップ目:半径CPの120°回転による軌跡
(ii)CA→AB
中心…頂点A
半径…AP=1
回転角…120°
よって、軌跡は\(2\pi × 1×\frac{120}{360}=\frac{2}{3}\pi\)

2ステップ目:半径APの120°回転による軌跡
(iii)AB→BC(正六角形の次の辺)
中心…頂点B
半径…BP=1
回転角…60°(=正六角形の内角ー正三角形の内角)
これより、軌跡は\(2\pi × 1×\frac{60}{360}=\frac{\pi}{3}\)

3ステップ目:半径BPの60°回転による軌跡
(i)、(ii)、(iii)より、軌跡は
\(\frac{2\sqrt{3}}{3}\pi+\frac{2}}{3}\pi+\frac{\pi}{3}=(1+\frac{2\sqrt{3}}{3})\pi\)
(i)〜(iii)の回転移動が、正六角形の辺の数だけ繰り返されるから、軌跡全体の長さは
\[
(1+\frac{2\sqrt{3}}{3})\pi×6=2(3+2\sqrt{3})\pi
\]
よって、5が正解である。





コメント