こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「位置関係」
対応関係に次ぐ頻出単元。
ここの対策を怠ると、かなり厳しいことになります。
ですが、ただ量をこなせばよい、というわけでもないのが難しいところ。
参考書を何回も解いたのに、過去問で手も足も出なかったときは相当ヘコんだ覚えがあります。

覚えるくらい解いても違う問題になると解けないのよね
闇雲に問題演習を重ねても、場当たり的な解き方しか身につかず、初見の問題には太刀打ちできません。
しかし、ご安心あれ。
数的処理の最難関である「国家総合職」の試験をパスした筆者が、位置関係の攻略に必須の考え方を伝授します。
それは、
【位置関係はジグソーパズル】
ということ。
今回は、数的処理の位置関係を解くコツを、過去問みたいな演習問題とともに紹介します。

一通りの基本は学んだけど、イマイチ点が取れない人向け
演習問題:おみくじに並ぶ列
ある神社では、6種類の運勢(大吉〜凶)が書かれたおみくじを販売している。この神社を訪れたA〜Fは、ある順番で列を作り、先頭の者からこのおみくじを1回ずつ引いた。A〜Fの中には子供を連れていた者もおり、同伴の子供も1回ずつおみくじを引いた。次のことが分かっているとき、確実に正しいといえるのはどれか。ただし、子供を2人以上連れていた者はいなかったものとする。
- Aの前後に並んでいた者およびEは、単独で神社を訪れていた。
- Bの後ろに並んでいた者は子供を連れており、その子供はCと同じ運勢であった。
- Cの前に並んでいた者はE、Cの後ろに並んでいた者はAであった。
- Dは子供を連れており、その子供の運勢は、2番目にくじを引いた者と同じであった。
- Fの前に並んでいた者は子供を連れており、その子供の運勢はFと同じであった。
- A〜Fの運勢は全て異なっていた。
- Aは子供を連れていた。
- Bの前後に並んでいた人はともに子供を連れていた。
- Cは先頭から3番目に並んでいた。
- Dは先頭に並んでいた。
- くじを引いた子供は全部で3人であった。
1
A〜F(+子供)によるおみくじの運勢の問題。
もうすぐ受験シーズンってことで。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:条件をピース化し位置関係を場合分け
文章題は、図や表で考えるのがキホン。
本問も、ひとまず条件を表に整理することを考えてみます。
条件や選択肢から、表の項目を決めます。
選択肢は全て「A〜Fの並び順」と「子供の有無」に関するもの。
このほか、条件は「運勢」にも触れています。
このことを踏まえ、次のようなフォーマットを用意します。
| A〜F | ||||||
| 子の有無 | ||||||
| 運勢 |

この表を埋めるのが目標ね
条件をピース化
条件を次のように「ピース化」すれば、本問はピース同士の位置関係を問う問題なのだ、ともいえます。
- Aの前後に並んでいた者およびEは、単独で神社を訪れていた。
- Bの後ろに並んでいた者は子供を連れており、その子供はCと同じ運勢であった。
- Cの前に並んでいた者はE、Cの後ろに並んでいた者はAであった。
- Dは子供を連れており、その子供の運勢は、2番目にくじを引いた者と同じであった。
- Fの前に並んでいた者は子供を連れており、その子供の運勢はFと同じであった。
- A〜Fの運勢は全て異なっていた。
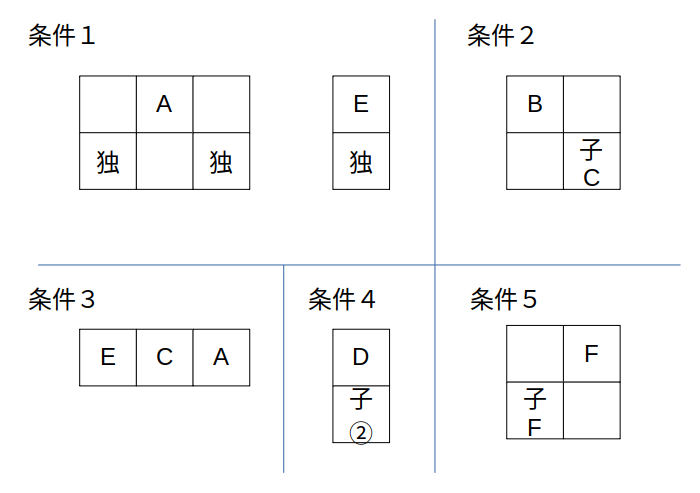
このうち、条件1&3は次のように合体させられます。
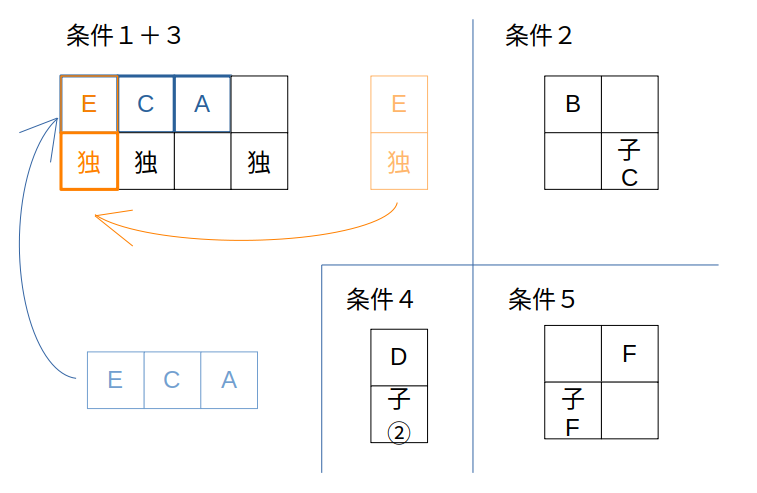

まるでジグソーパズルみたいね
位置関係には鉄則があります。
それは、制約の厳しい条件から手を付ける、というもの。
本サイトでは、「解法のポイント」として繰り返し伝えています。
文量の多い条件に注目
本問なら、カバーする領域が広い(=制約が厳しい)のは明らかに条件1+3。
ここに残りのピース(2と4と5)を当てはめていきます。
まさに、【位置関係はジグソーパズル】。
Bの位置で場合分け
残ったピースのうち、サイズが大きい(=制約が厳しい)のはBの条件(or Fの条件)。
定石通り、Bのピースを当てはめることを考えます。

Dの条件よりもカバーする範囲(マス数)が多い
「ECA」というカタマリに対し、Bの位置としてあり得るのは次のいずれかです。
(i)Eの2つ前(B○ECA○)
(ii)Eの前(○BECA○)
(iii)Aの後ろ(○ECAB○ or ECAB○○)
(iv)Aの2つ後ろ(ECA○B○)

6人の列なら、「B○○ECA」と「ECA○○B」もあるんじゃない?
それらは、いずれも条件を満たせません。
B○○ECA→Aが最後尾、Aの条件に反する
ECA○○B→Bが最後尾、Bの条件に反する
【位置関係はジグソーパズル】の考え方だと、どちらもピースが後ろにはみ出します。

書いてみると分かるよ
上の場合分けでも、AまたはBが最後尾となるパターンは外してあります。
(i)BがEの2つ前→×:Dの子の条件で矛盾
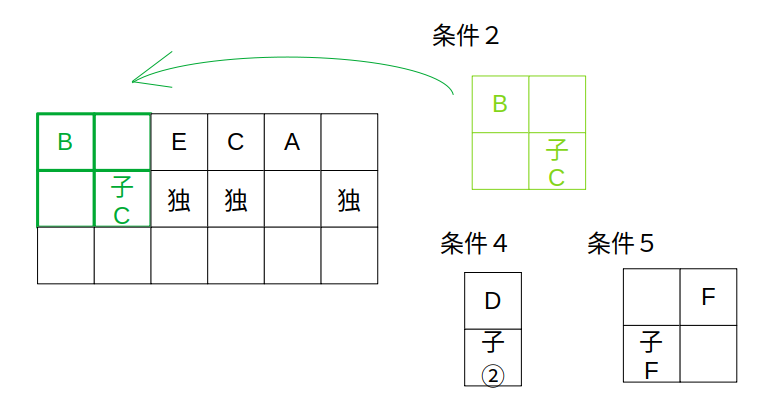
Fのピースが入る場所を考えます。
Fの位置は、Bの後ろかAの後ろのいずれかです。
仮にBの後ろとしてみます。
すると、DはAの後ろ。
が、Aの後ろは単独なので、Dのピースは入りません。
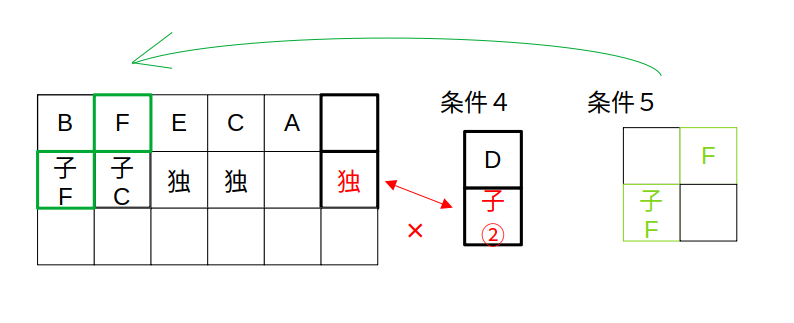
では、Aの後ろならどうか。
今度はDがBの後ろになります。
Dは子連れで、その子供の運勢は2番目、つまりDと同じです。
ところで、Bの条件によれば、Bの後ろの子供の運勢はCと同じ。
これらを同時に満たすには、運勢が「C=D」でなければなりません。
これは6つ目の条件「A〜Fの運勢は全て異なっていた。」に反します。
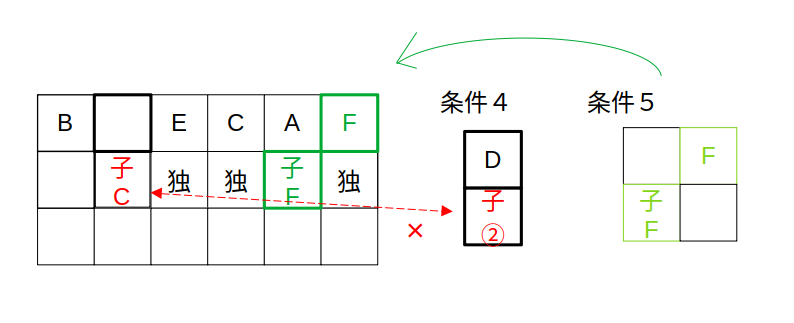

つまり、(i)はあり得ない
(ii)BがEの前:Eの子の有無で矛盾
【位置関係はジグソーパズル】の考え方だと、BのピースはEの前にはハマりません。
Bの条件だと「後ろが子連れ」ですが、Eは単独で訪れているからです。
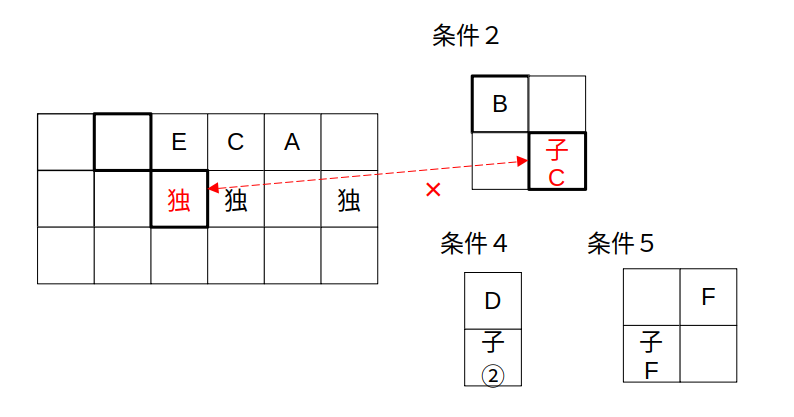

(ii)はあり得ない、ということ
(iii)BがAの後ろ:Eが先頭か否かで場合分け
この場合、(iii-a)「○ECAB○」あるいは(iii-b)「ECAB○○」です。
(iii-a)「○ECAB○」→×:Fのピースがハマらない
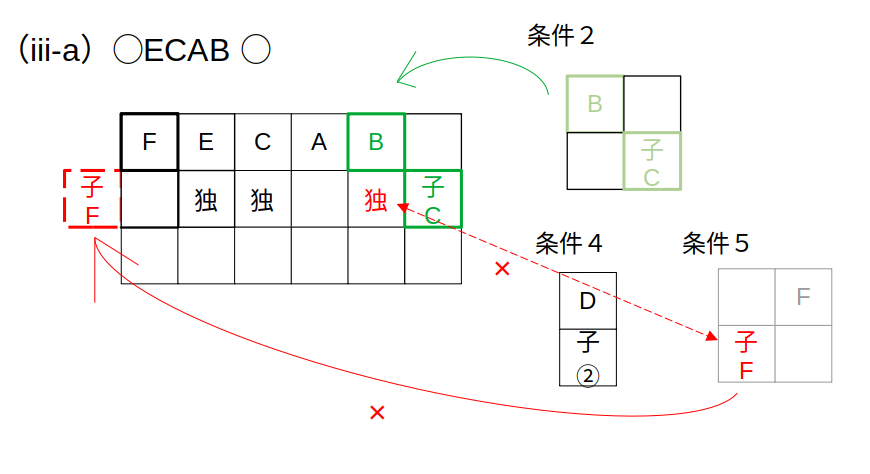
Fの位置を考えます。
Eの前だとすると、ここは先頭なのでFの条件を満たしません。
【位置関係はジグソーパズル】でいえば、Fのピースが前にはみ出す、ということ。
Bの後ろはどうでしょう。
Bは単独なので、やはりFの条件を満たせません。

ピースが干渉してしまうから条件に反する
(iii-b)「ECAB○○」→×:Fの前の子の条件で矛盾
やはりFの位置から。
まず、Bの後ろは条件に合いません。
Bは単独なので、Fの条件「Fの前は子連れ」を満たせないからです。
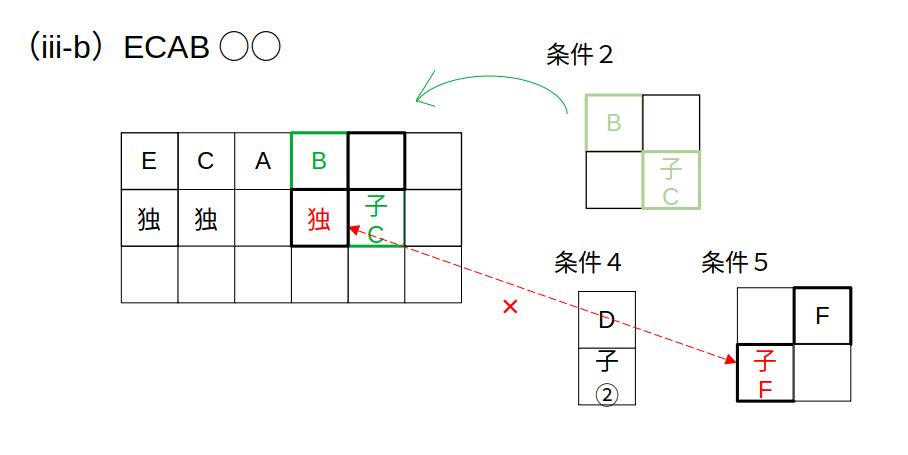
とすると、FはBの2つ後ろ?
その場合、残るDはFの前です。
このとき、Dの子供の運勢はCと同じになります。
これはBの条件に矛盾しません。
が。
Fの条件によると、Dの子供の運勢はFとも同じのはず。
つまり運勢が「C=F」でなければならず、6つ目の条件「A〜Fの運勢は全て異なっていた。」に反します。
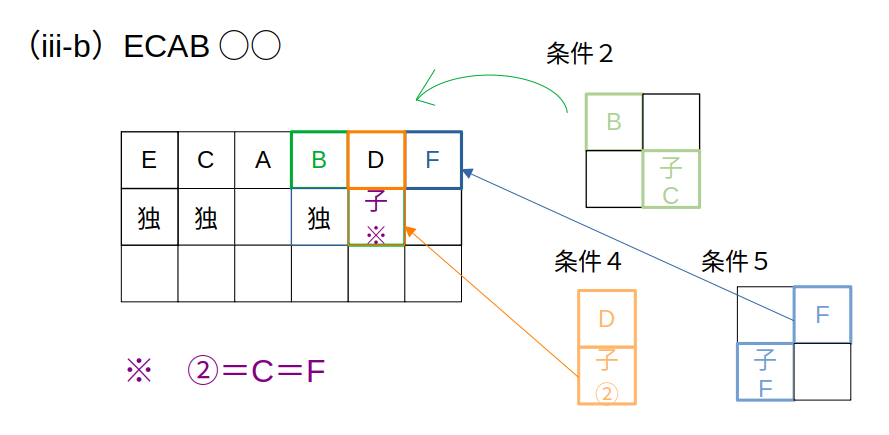

(iii)も可能性がないことになる
(iv)BがAの2つ後ろ:Dが最後尾なら◎
やはりFの位置から。
FがAの後ろだったとすると、DはBの後ろ。
Dの子供の運勢はC(2番目)なので、条件を満たします。
ほかも矛盾はありません。
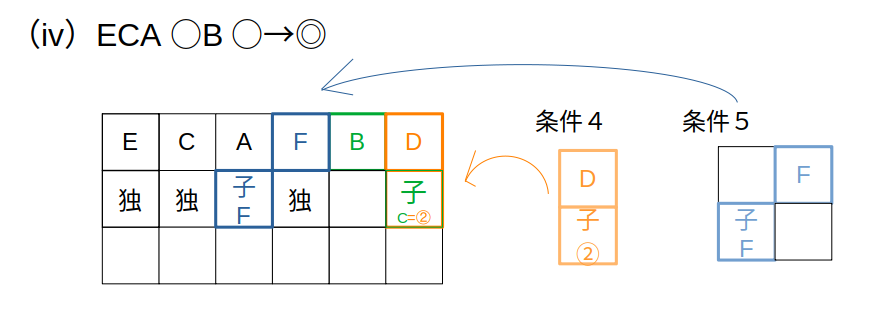
念のため、FがBの後ろだった場合も検討しますと……
この場合、DがAの後ろになりますが、ここは単独なので「Dは子連れである」という条件を満たせません。
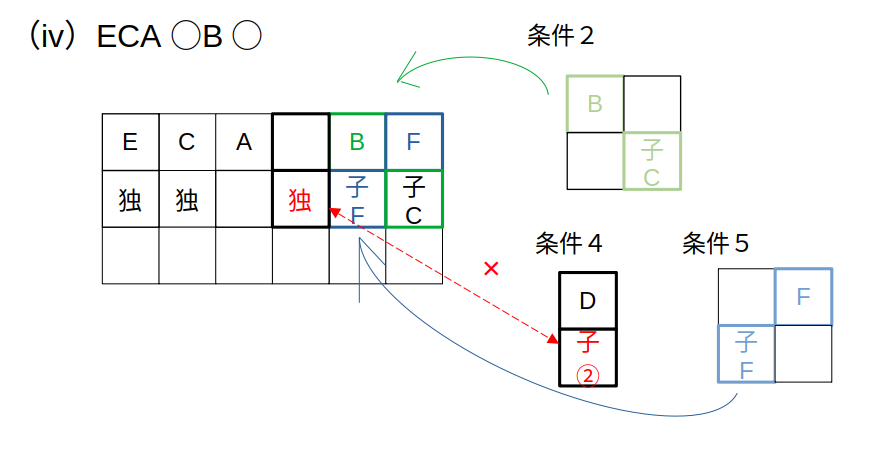

「ECAFBD」が唯一の正解パターン
Aは子連れなので、選択肢1は正しいといえます。
以上より、1が正解です。
おわりに:位置関係は条件のパズル
お疲れ様でした!
【位置関係はジグソーパズル】です。
条件を「ピース化」し、一つずつ当てはめていきます。
ピースが全てハマるパターンを探すのが目標。

OK/NGが直感的に分かるのがメリット
今回は、おみくじに並ぶ列の位置関係の問題でした。
位置関係含め、文章題は「何を調べるか」をハッキリさせるのが重要。
条件と選択肢を見て決めましょう。
ちなみに、A〜Fの運勢(大吉〜凶)を具体化する必要はありません。
中吉と吉、どちらが上か知らなくても問題ナシ。
中吉〜末吉の序列は寺社によって変わるらしいよ

ネットで絶えずマウント合戦してそう
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
「A〜F」の「子供の有無」と「運勢」を明らかにするため、次のような表のフォーマットを用意する。
| A〜F | ||||||
| 子の有無 | ||||||
| 運勢 |
ここに、次のような条件の「ピース」を当てはめることを考える。

条件をピース化する
条件1&3は、次のように合体させられる。

A&C&Eのピースを合体A&C&Eのピースを合体
以下、Bの位置で場合分けする。
(i)Eの2つ前(B○ECA○)
(ii)Eの前(○BECA○)
(iii)Aの後ろ(○ECAB○ or ECAB○○)
(iv)Aの2つ後ろ(ECA○B○)
(i)Eの2つ前(B○ECA○)
仮にFをBの後ろとすると、DはAの後ろである。
しかし、Aの後ろは単独である、という条件に反するので不適。

(i)Dが最後尾→子の有無で矛盾
FをAの後ろとすると、DはBの後ろで、Dの子の運勢はDと同じ。
Bの条件「Bの後ろの子供の運勢はCと同じ」を満たすには、運勢がC=Dである必要がある。
これは6つ目の条件「A〜Fの運勢は全て異なる」に反するので不適。

(i)Dが2番目→子の運勢で矛盾
(ii)Eの前(○BECA○)
Bの条件「後ろが子連れ」が、Eは単独であったことに反するので不適。

(ii)Bが2番目→Eの子の有無で矛盾
(iii)Aの後ろ(○ECAB○ or ECAB○○)
(iii-a)○ECAB○
Fの位置がEの前だと、先頭なのでFの条件「前は子連れ」を満たさない。
Bの後ろも、Bは単独だからFの条件を満たさない。

(iii-a)Fのピースが条件を満たせない
(iii-b)ECAB○○
Fの位置ついて、Bは単独なので、Fの条件「前は子連れ」を満たせるのはBの2つ後ろだけ。
このとき、Dの子供の運勢はCと同じ、かつFとも同じとなるが、これは6つ目の条件「A〜Fの運勢は全て異なる」に反する。

(iii-b)Fが最後尾→Dの子の運勢で矛盾
(iv)Aの2つ後ろ(ECA○B○)
Fの位置がAの後ろだったとすると、DはBの後ろで、Dの子供の運勢はC(2番目)となる。

(iv)Bが5番目→◎
FがBの後ろだった場合、Aの後ろ(D)は単独なので、Dの条件「Dが子連れ」に反する。

(iv)Fが最後尾→Dの子の有無で矛盾
以上より、1が正解である。




コメント