こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます!
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。
そろそろこのサイトにもプライバシーポリシーのページを作らなくては。
前回は、旅行会社の社員が観光地を5段階で評価する問題をやりましたね。
国家総合職の数的処理に必須の、数量の関係を論理的に思考して明らかにする力が身につくので、解いてない方はぜひ挑戦してみてください。
もう解いた方は、解法を思い出せますか?
問題を解いたあとは、要点だけでも思い出すクセを付けてみてください。
思い出すだけなら頭一つでできますし、時間もそんなにかからないのでおすすめです。
新しく問題を解くのは大切ですが、解いたら必ず復習もセットで行うようにしましょう!
復習がバッチリな方は、本日の問題へ参りましょう。
本日の演習問題
200以下の3桁の自然数A、B、Cについて、次のことが分かっているとき、B-Aはいくらか。
- B>A>Cである。
- AとB、BとC、CとAの最大公約数は、それぞれ2、18、14である。
- Aは10で割り切れる。
- BとCの積は77で割り切れる。
- 46
- 58
- 65
- 72
- 83
2
3つの整数を特定する問題です。
「最大公約数」や「割り切れる」というヒントをもとに、整数を決定しましょう。
以下、詳しい解説になります。
回りくどい説明が嫌な方は、一番下に略解としてコンパクトにまとめてあるので、そこだけ読んでいただくのでも大丈夫です。
それではスタート!
詳しい解説
条件「AとB、BとC、CとAの最大公約数は、それぞれ2、18、14である」から手を付けます。
AとBの最大公約数が2、ということは、AとBを素因数分解するとそれぞれに2が(少なくとも)1つずつ表れるということです。
同様に、BとC、CとAはそれぞれ18(=2×3×3)、14(=2×7)を1つずつ約数に持ちます。
ここまでをまとめると以下のようになります。
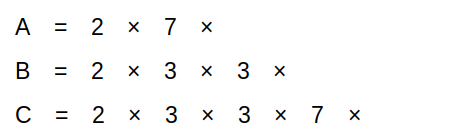
次に、条件「BとCの積は77で割り切れる」を考えてみます。
これは、整数「B×C」は77(=7×11)を約数に持つ、ということです。
BとCを掛け算した結果、77を約数に持つことになったのですから、BとCのいずれかが7および11をはじめに約数として持っていたことになります。
いま、Cが7を約数に持つことはすでに確定済みですから、BかCの少なくともどちらか一方が11を約数に持っていなければなりません。
Cが11を約数に持っていたとすると、C=2×3×3×7×11=1386となり、「200以下」という条件に反します。
したがって、Cが11を約数に持つことはなく、Bが11の約数を持つことが確定します。
ここで、Bが11だけでなく7も約数に持っていた場合も、「B×C」は77で割り切れることになりますが、これはどうでしょうか?
結論からいうと、Bが7を約数に持つことはありません。
理由はCが11を約数に持たないことを示したときと同様で、B=2×3×3×11×7とするとB=1386となり200をオーバーするからです。
実は、この時点ですでにBとCの値は確定します。
まず、現時点でB=2×3×3×11×?ですが、?に入る数字を2とすると、B=2×3×3×11×2=396より、200をオーバーするので、?には1しか入りません。
Cについても全く同じで、C=2×3×3×7×?において?を2とするとC=252となって200を超えるので、?には1しか入りません。
よって、B=2×3×3×11=198、C=2×3×3×7=126、と確定します。
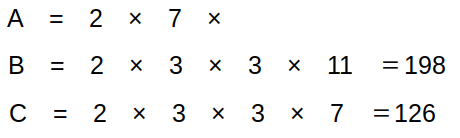
あとはAですが、条件「Aは10で割り切れる」から決定します。
Aは10(=2×5)を約数に持つので、5が約数として新たに加わってA=2×5×7×?となります。
BとCのときのように、?を2としてみると、A=2×5×7×2=140となり、「200以下」の条件を満たします。
次に?を3としてみると、A=2×5×7×3=210となり、200をオーバーするのでダメですね。
これにより、A=2×5×7×2=140が正しいと分かります。
(?が1の場合、A=2×5×7×1=70より、3桁にならないので不適)
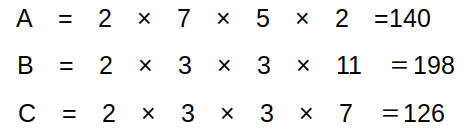
これより、B-A=198-140=58なので、2が正解です。
おわりに
お疲れ様でした!
いかがだったでしょうか?
ヒントに従い順を追って考えれば、比較的スムーズに解答できたのではないでしょうか。
整数問題としては標準〜やや簡単、くらいの難易度だと思います。
本番で出題されたらぜひとも得点しておきたい問題ですね。
本問くらいの難易度の問題をいち早く片付けて、浮いた時間を判断推理など手数の多い問題に注力することが、教養試験に対する戦略の基本となります。
よく巷では「数的処理は1問を3分半で解かなければならない」と言われますが、これは半分正解で半分間違いだと思います。
実際に過去問を見てみると、特に国家総合職では3分半以内に解ける問題はそう多くないことが分かります。
だからこそ、タイムマネジメントが重要になってきます。
3分半、というのは恐らく数的処理にかけられる総時間を単純に問題数で割った時間ですが、実際の現場では3分半以上は優にかかる問題もあれば、本問のように短時間で終えられる問題もあるのです。
そういった問題を落とさず、かつ迅速に片付ければ、問題によっては3分半以上かけてもよいものだってあります。
なるべく短時間で、という意識は正しいですが、3分半、という数字にはあまりとらわれなくても大丈夫です。
本番では、いわゆる「捨て問」もあるので、そういった問題に引っかからなければもう少し余裕をもって問題に当たることができます。
一問一問時間を計って解いている方もいるかと思いますが、3分半をオーバーしても落ち込まなくて大丈夫です。
それよりも、捨て問をきちんと見分けられるようになる方が重要かもしれません。
本サイトで問題を解くときは、「本番だったら解くべきか?」という点も意識してみてください。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
いいねボタンだけでも押して行っていただけると、投稿の励みになりますので、ぜひポチッとよろしくお願いします!
次回もお楽しみに!
略解
条件「AとB、BとC、CとAの最大公約数は、それぞれ2、18、14である」より、AとBとCをそれぞれ素因数分解した形は、途中までで次のように書き表せる。

ABCの素因数
次に、条件「BとCの積は77で割り切れる」について、Cが7を約数に持つことから、BとCのいずれかあるいは両方が11を約数に持つことになる。
ところが、Cが11を約数に持っていたとすると、C=2×3×3×7×11=1386>200となり条件に反する。
よって、11を約数に持つのはCではなくBである。
ここで、Bが7を約数に持つ可能性について検討する。
仮にBが7を約数に持つとすると、B=2×3×3×11×7=1386>200なので不適。
よって、Bが7を約数に持つことはない。
この時点でB=2×3×3×11×?であるが、?に入る数字を2とすると、B=2×3×3×11×2=396>200より、不適。
よって、B=2×3×3×11=198
Cについて、同じくC=2×3×3×7×?において?を2とするとC=252>200なので、?には1しか入らず、C=2×3×3×7=126
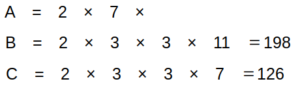
BとCが確定
また、条件「Aは10で割り切れる」より、Aは5を約数に持ち、A=2×5×7×?
?が1のとき、A=70<100となって不適。
?が2のとき、A=140となり、条件を満たす。
?が3のとき、A=210>200より、不適。
以上から、?は2しかあり得ず、A=2×5×7×2=140

整数ABCが決定
これより、B-A=198-140=58
したがって、正解は2である。

コメント
大変面白い問題だと思ったのですが、B=2×3×3×11なので、これを計算すると132ではなく198となってしまいます
おそらく、2×2×3×11=132になりますが、その場合BCの最大公約数が18ではなく12になってしまい、かつCも2×2×3×7としなくてはならず、さらにはAとBの最大公約数も2ではなく4となります
コメントありがとうございます。
こちらで確認したところ、Bの値の計算を間違えていたようでした。
おっしゃる通り、正しくは「B=198」です。
これに伴い、AとBの大小関係の条件を「B>A>C」に修正し、選択肢のラインナップも変更して、B-A=58で2番が正解、としました。
私の計算ミスが混乱を招き、申し訳ございません。
ご指摘に感謝いたします。
よろしければ他の問題も見ていってください。
そしてお気づきのことなどあればコメントください!