こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「面積比(平面図形)」
面積比の解き方は主に2つ。
次のいずれかを利用するものです。
- 底辺 or 高さの比
- 相似比
今回は、これらに次ぐ第三の解き方を紹介!
それは……
【等しい角をはさむ辺の比】
この解き方を知ってると、もっと簡単に面積比を求められる場合があるんです。
今回は、平面図形の「面積比」を解く2+1つの方法を、ていねいに解説します。
後半では、数的処理の過去問に似せた演習問題を解きながら、その使い方を学びます。
講義:面積比の解き方2+1パターン
面積比は、2+1通りの求め方があります。
定番なのは、「底辺 or 高さの比」と「相似比」を使う方法。
面積比の求め方その1:底辺 or 高さの比
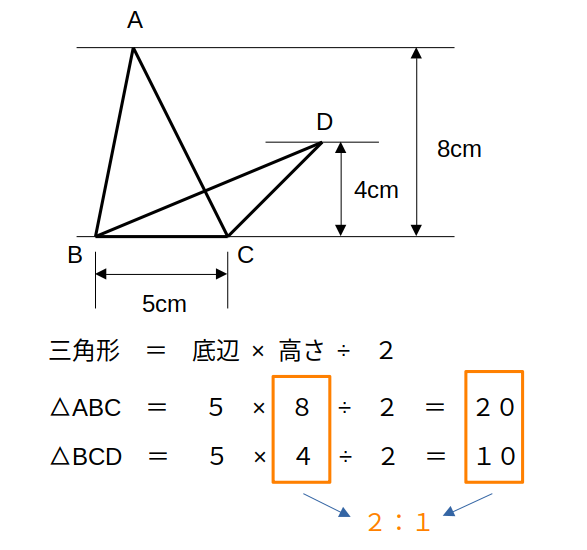
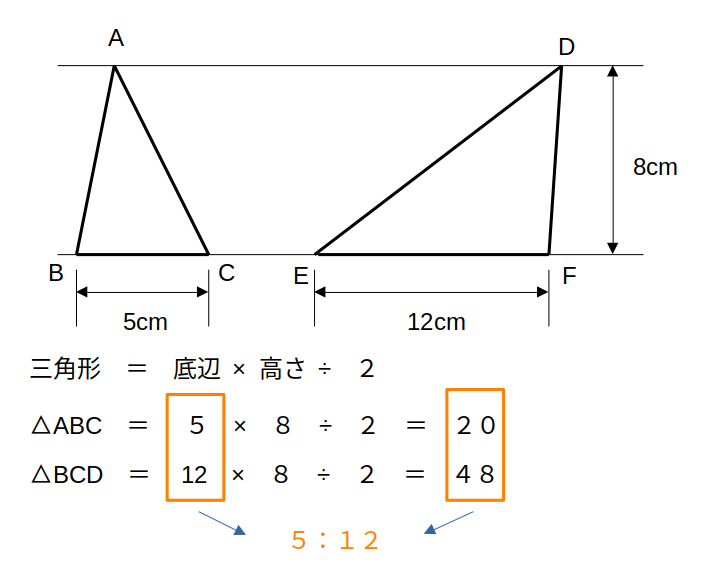
底辺の長さが等しい → (面積比)=(高さの比)
高さが等しい → (面積比)=(底辺の比)
これは、三角形の面積公式に基づいています。
面積比の求め方その2:相似比
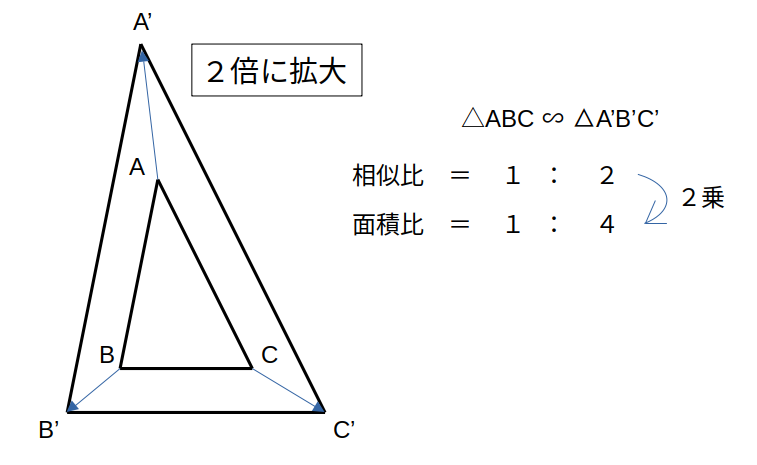
相似なら、相似比の2乗が面積比です。
つまり、(相似比)=a:bなら、(面積比)=a2:b2
【面積比の解き方3:等しい角をはさむ辺の比】
第3の解き方。
これは、等しい角がある場合に使える解き方です。

よくあるのは、角を共有してるケース
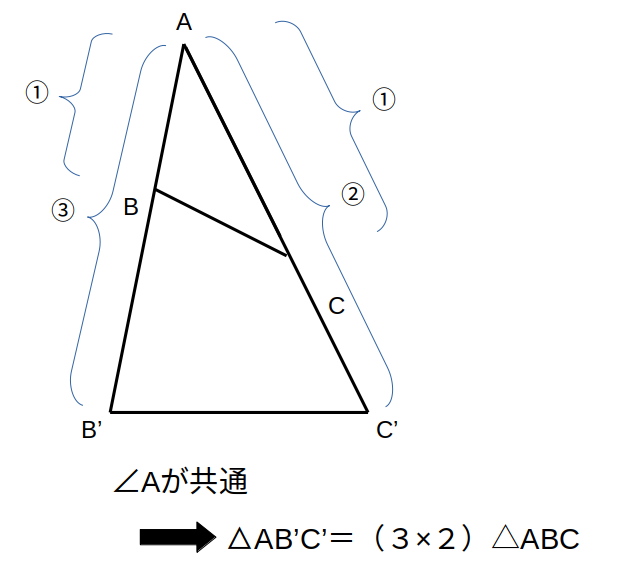
これは、もう一つの面積公式に基づいています。
「三角形の面積は、1つの角とはさむ2辺の長さで決まる」というもの。
高校数学の公式です。
三角形の面積公式:
\[
△\mathrm{ABC}=b×c×\sin{\mathrm{A}}
\]
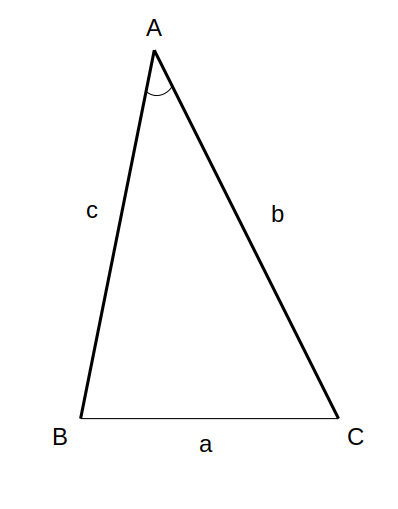

\(\sin{\mathrm{A}}\)は、角の大きさで決まる数です
この解き方を使うと、面積比をもっと簡単に求められる場合があります。
次の例を見てください。
例題:平行四辺形の内部の面積比
図のような平行四辺形ABCDにおいて、四角形CDEFの面積は平行四辺形ABCDのそれの何倍か。
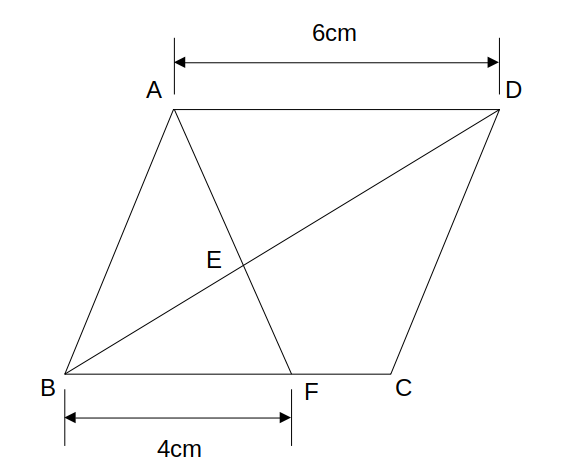
問題の設定は、下記のサイトからお借りしました。
子どもを混乱させる相似な三角形の2つの面積比 – 算数数学が苦手な子専門のプロ家庭教師みかん先生
底辺・高さの比や相似比を使った解き方は、リンク先で丁寧に解説されているので割愛。
ここでは、代わりに【等しい角をはさむ辺の比】を使った解き方を紹介します。
【等しい角をはさむ辺の比】で解く
対角線BDに対して、△BCD=\(\frac{1}{2}S\)

\(S\)は平行四辺形の面積ね
次に、△BEFの面積。
△BCDと△BEFは∠Bを共有しています。
【等しい角をはさむ辺の比】の使いどころです。
まず、BC:BF=6:4=3:2
さらに、△BEF∽△DEAなので、BE:ED=2:3
つまり、BD:BE=5:2
これより、△BEF=\(\frac{2}{3}×\frac{2}{5}\)△BCD=\(\frac{4}{15}\)△BCD
よって、四角形CDEF=(1-\frac{4}{15})△BCD=\(\frac{11}{15}×\frac{1}{2}S\)=\(\frac{11}{30}S\)
以上より、四角形CDEFは平行四辺形ABCDの\(\frac{11}{30}\)倍
結論:共通角の面積比は辺の比で
この解き方を使うメリットは、相似比だけで面積比が分かること。
底辺・高さの比や相似比で解く場合、「△ABD→△ADE(底辺の比)→△BEF(相似比)→四角形」という流れになります。
対し、今回の解き方なら、必要なのは相似比だけ。
等しい角を見つけたら、使ってみてください。
以上、【等しい角をはさむ辺の比】から面積比を求める方法の解説でした。
ここからは、数的処理の過去問みたいなオリジナルの演習問題を解きながら、解法の使い方を学んでいきます。
演習問題:正六角形の内部にある三角形の面積
図のように、正六角形ABCDEFの辺ABおよびAFの中点P、Qを結び、PQがACおよびAEと交わる点をそれぞれR、Sとする。正六角形ABCDEFの面積を1とするとき、△APRの面積はいくらか。
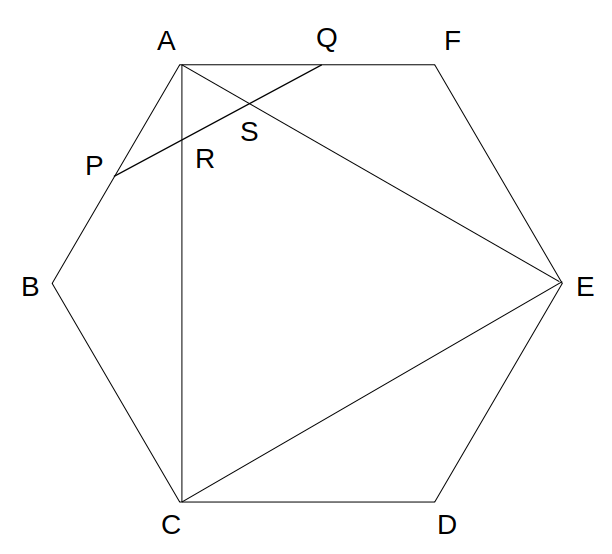
- \(\frac{1}{24}\)
- \(\frac{1}{36}\)
- \(\frac{1}{48}\)
- \(\frac{1}{60}\)
- \(\frac{1}{72}\)
5
正六角形の内部にある三角形の面積の問題。
面積比だと気づいてからが本番です。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:正六角形を1とする面積比
面積の問題は、主に2通りの解き方があります。
- 大きさが分かっている図形との相似比から求める方法
- 具体的に長さを求めて面積公式に当てはめる方法
本問は、「正六角形に対して△APRの面積は何倍か?」という問題なので、面積比のパターン。

長さが一切与えられてないから「公式で求める」は無理
以下、面積比を考えていきます。
補助線を引いて正六角形を6等分
平面図形といえば、補助線。
ここでは、BとFを結びます。
その上で、正六角形の定石「6等分」を使います。
対角線を引くと、6つの正三角形に分けられます。
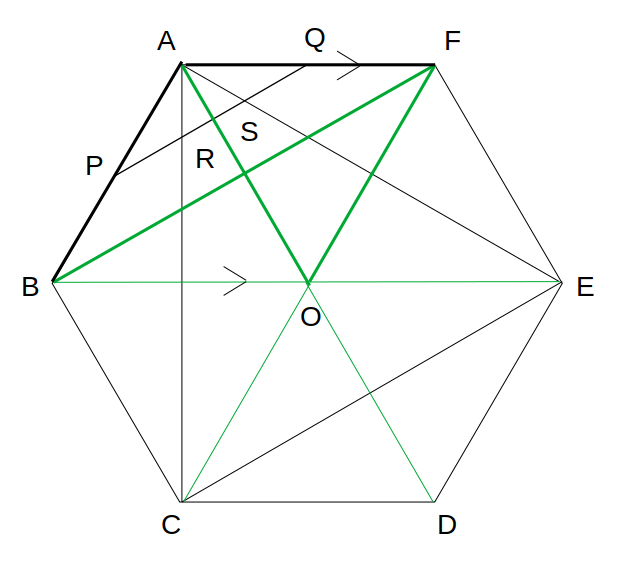
すると、AF//BEなので、△ABF=△OAF=\(\frac{1}{6}\)

底辺も高さも共通
共通角なら辺の比で面積比が分かる
さらに、∠Aに注目。
ここで【等しい角をはさむ辺の比】が登場します。
△APQ=\(\frac{1}{2}×\frac{1}{2}\)△ABF=\(\frac{1}{24}\)

PQ//BFなので△APR∽△ABF、と考えてもいい
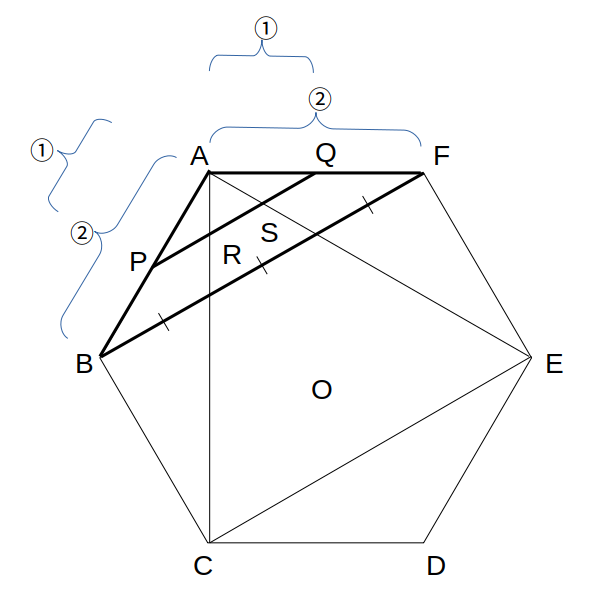
ここで、△APRと△AQSは二等辺三角形、かつ△ARSは正三角形。
つまり、AR=RS=SQ(なぜ?→補講)
かつ、高さが共通なので、面積は全て等しい。
したがって、△APR=\(\frac{1}{3}\)△APQ=\(\frac{1}{72}\)
よって、5が正解です。
補講:△APQはホントに3等分なの?
疑問を持つのは素晴らしいこと。
次の2ステップで、AR=RS=SQを示します。
- △ARSは正三角形
- △APR(&△AQS)は二等辺三角形
1.△ARSは正三角形
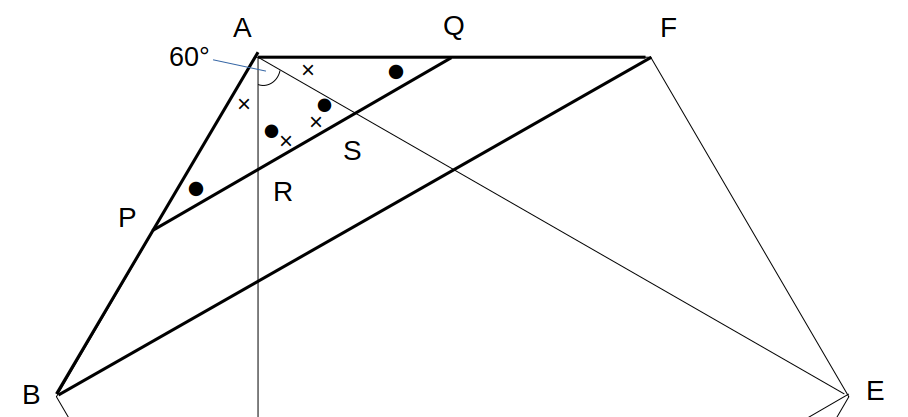
三角形の内角と外角の関係より、
∠ARS=∠APR+∠PAR=●×
∠ASR=∠AQS+∠QAS=●×
△ARSの内角について、60°+∠ARS+∠ASR=180°
つまり、2●×=120°
→●×=60°
これは、△ARSが正三角形であることを示します。(内角が全て60°)
2.△APR(&△AQS)は二等辺三角形
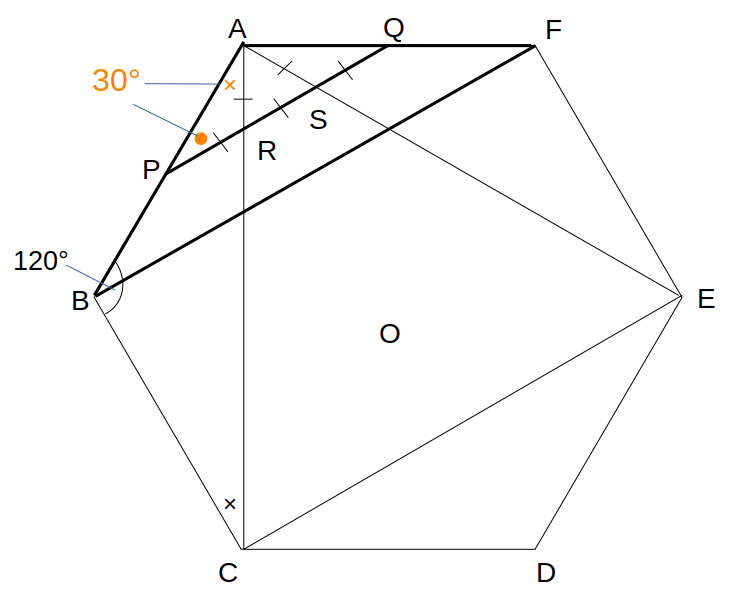
△ABCに注目。
AB=BCの二等辺三角形で、∠BAC=∠BCA=×
正六角形の内角は120°なので、
×+120°+×=180°→×=30°
∠ARPは正三角形の外角で120°なので、∠APR=30°
→△APRは二等辺三角形で、AR=PR
△AQSも、全く同様にAS=QS
以上より、AR=RS=SQ
おわりに:共通角の面積比なら辺の比もアリ
お疲れ様でした!
面積比の解き方は、「底辺・高さの比」と「相似比」と、もう一つ。
【等しい角をはさむ辺の比】でも求められます。
等しい角度、特に共通角の三角形に有効です。
覚えておくと吉。
今回は、正六角形の内部にある三角形の面積を求める問題でした。
正六角形を1としていることより、面積比の問題だと判断できます。
「6等分」と「補助線」ができたら、あとは定石通り。
中点連結定理を知ってれば、相似比で考えることもできます。
レジで考え事してたらレシートじゃなくて釣り銭を捨てそうになった

MP5(マジでポイする5秒前)
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
補助線BFを引く。
さらに、対角線により正六角形ABCDEFは6つの正三角形に等分される。
AF//BEなので、△ABF=△OAF=\(\frac{1}{6}\)

補助線&6等分
∠Aは共通なので、
△APQ=\(\frac{1}{2}×\frac{1}{2}\)△ABF=\(\frac{1}{24}\)
ここで、△APRと△AQSは二等辺三角形、かつ△ARSは正三角形である。
つまり、AR=RS=SQ
高さが共通なので、△APR=△AQS=△ARS

共通角なら辺の比&底辺の3等分
これより、△APR=\(\frac{1}{3}\)△APQ=\(\frac{1}{72}\)
よって、5が正解である。



コメント