こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「正多面体の面・頂点・辺の数」
空間図形で頻出の正多面体。
覚えていれば解ける問題もあるので、苦手な人もココだけは勉強してほしいところ。
逆に、勉強はしているけど、覚えられなくて困ってるんだ!という人もいるでしょう。

頂点の数?辺の数?まったく覚えられん
そういう人にオススメなのが、【その場で導き出す】というアプローチ。
今回の「面・頂点・辺の数」は、数そのものを丸暗記する必要はありません。
むしろ、大切なのは「数え方」。
数え方を理解していれば、いつでも計算できます。

理解した考え方を使って問題が解けることもあるよ
正多面体の面の数・辺の数・頂点の数の数え方は、以下の記事で解説しています。
今回は、このアプローチが使える問題を用意しました。
以下、過去問をもとに作ったオリジナルの演習問題を解きながら、「解法のポイント」の使い方を学んでいきます。
演習問題:双対な関係にある正多面体
以下の説明文の空欄A〜Cを埋める語句の組み合わせとして正しいのは次のうちどれか。
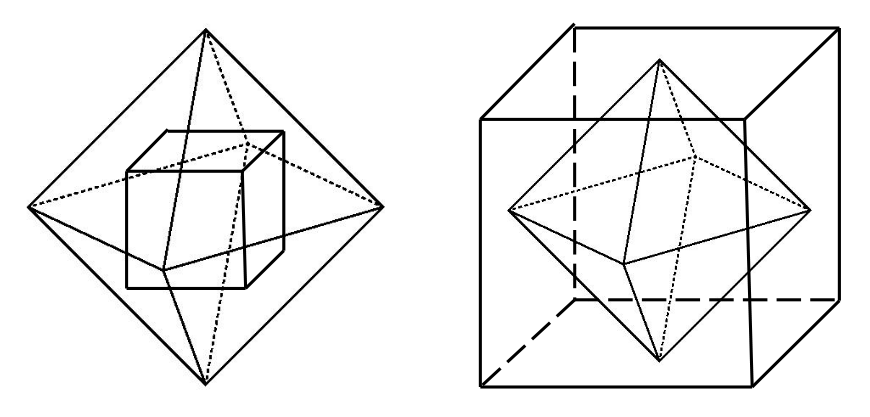
立方体の隣り合う面の中心を結んでできる立体は正八面体であり、正八面体の隣り合う面の中心を結んでできる立体は立方体である。このとき、両者は「双対な関係にある」という。
いま、正十二面体と双対な関係にある立体を考えると、この立体の頂点の数は( A )。よって、この立体の一つの頂点に集まる面の数は( B )であり、この立体の頂点を切り落とした切断面は( C )となる。
| A | B | C | |
| 1. | 12 | 3 | 正三角形 |
| 2. | 12 | 5 | 正五角形 |
| 3. | 20 | 3 | 正五角形 |
| 4. | 20 | 4 | 正方形 |
| 5. | 20 | 5 | 正五角形 |
2
立体の双対性をテーマとした空欄補充問題。
知ってれば即答できますが、知らなくても解けます。
以下、詳しい解説。
あっさりした解説がお好みの方は、一番下の略解を見てね。
おっと申し遅れました。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介
それでは、解説スタート!
解説:正多面体の頂点はその場で数える
A:双対なら頂点の数は面の数
「双対な関係にある」の意味は、問題文の通り。
これによると、立体αとβが双対な関係にあるなら、αの面の数はβの頂点の数に一致します。
逆に、αの頂点の数はβの面の数に一致します。
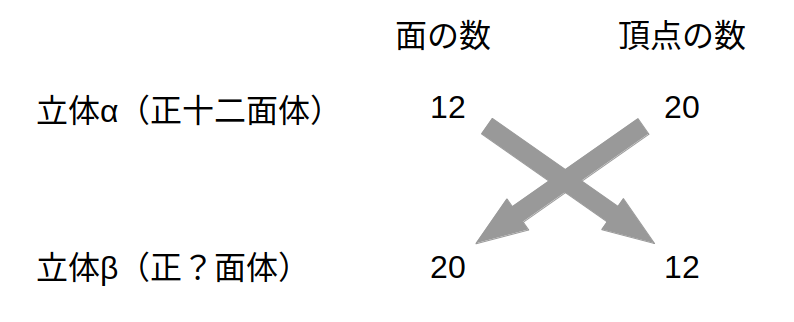
よって、正十二面体と双対な立体の頂点の数は、正「十二」面体の12……A
B:正多面体の頂点の数をその場で求める
次の公式を使うと、一つの頂点に集まる面の数(B)が分かります。
頂点の数=1面の頂点の数×面の数÷頂点に集まる面の数
頂点の数(=12)は分かっているので、あとは「1面の頂点の数」と「面の数」。
「面の数」は、正十二面体の頂点の数(=20)です。
これは、覚えてなくても簡単に計算できます。
正十二面体は、12枚の正五角形でできています(12×5)。
各頂点は3つの正五角形が重なる(÷3)ので、
12×5÷3=20 ← 公式そのもの!

暗記もいいけど「なぜそうなるか?」を理解してほしい
双対な立体とは、正二十面体のことでした。
正二十面体の面は正三角形なので、「1面の頂点の数」は3。

正十二面体は五角形であとは三角形、と覚えればOK
頂点の公式より、12=3×20÷(頂点に集まる面)
→(頂点に集まる面)=5……B
C:頂点周りの面の数=切り口の辺の数
頂点に5つの面が集まっている、というのは、次の図のような状態。
これを切り落とすとき、切る面は頂点の周りの面と線で交わります。
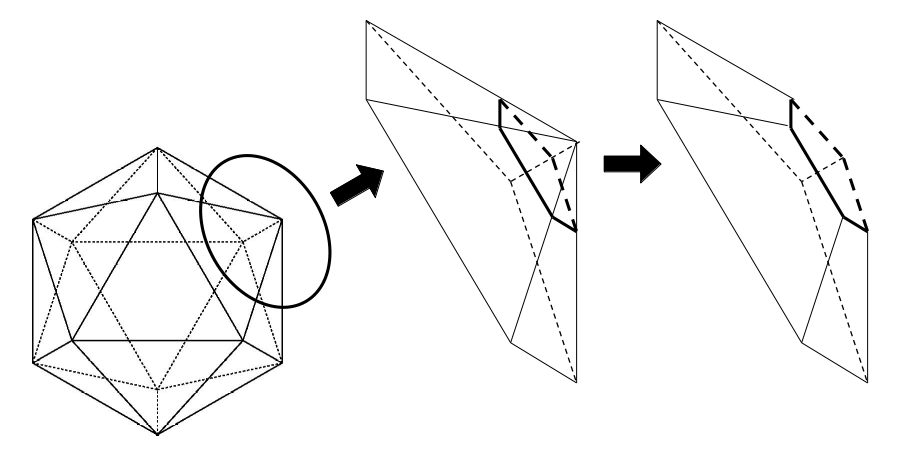
つまり、切り口は5つの辺で囲まれた「正五角形」……C
以上、まとめると
A:12
B:5
C:正五角形
よって、2が正解です。
おわりに:正多面体の面・頂点・辺の数は「理解する」
お疲れ様でした!
正多面体の面・頂点・辺の数は、覚えずとも【その場で導き出す】ことができます。
「なぜそうなるか?」を理解してればOK。
なかなか覚えられない方は、理詰めもアリ。

丸暗記が苦手な筆者は、理屈を重視してました
今回は、正二十面体の面・頂点の数の問題でした。
双対な関係の性質を使うのが第一歩。
正十二面体の頂点の数は、覚えてなくてもすぐに計算できます。
頂点の数の公式も含め、成り立ちを理解しているのが理想。
アンパンマン!新しいクレカよ!

クレジットカードの更新時期でした
最後までお読みいただきありがとうございました。
本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください!
この記事が参考になったら、ぜひシェアしてください!
Tweet次回もお楽しみに!
略解
双対な関係の性質より、正十二面体と双対な立体の頂点の数は12……A
一つの頂点に集まる面の数(B)は、次の公式で求める。
頂点の数=1面の頂点の数×面の数÷頂点に集まる面の数
「面の数」は、正十二面体の頂点の数、すなわち20。
→双対な立体は正二十面体
正二十面体の面は正三角形なので、「1面の頂点の数」は3。
よって、12=3×20÷(頂点に集まる面)
→(頂点に集まる面)=5……B
頂点を切り落とすとき、切る面は周りの5面と交わる。
つまり、切り口は「正五角形」……C

正二十面体の頂点の切断面
よって、2が正解である。




コメント