こんにちは!
公務員試験の数的処理解説サイト「数的処理の穴場」へようこそ。
【2】どこよりも詳しい解説
【3】誰でもすぐに使える「解法のポイント」
を扱う、ありそうでなかった数的処理の学習サイトです。
公務員試験の数的処理をはじめとした、算数/数学の試験を受ける方は必見!
ぜひ最後まで読んでいってください。

「解法のポイント」はないこともある、かもしれない
今回のテーマは……「立体の回転(立体図形)」
立体図形でよくあるのが
平面上で滑らないように立体を転がす、という問題。
実は、こうした問題にはコツがあります。
それは「立体のまま考えない」ということ。

どういうことや?
3Dがダメなら2Dで。
つまり
平面でとらえよう
ってこと。
そのために必要なカギは2つ。
今回は、転がる正四面体の攻略法をていねいに解説します。
この記事のココがスゴイ!
- 転がる正四面体の解き方を基本からおさらいできる(簡単な例題つき)
- 転がるアニメーションを使った「目で分かる」解説!
- 元塾講師による、オリジナル問題の【世界一ていねいな解説】!

基礎が一通り終わって、そろそろ過去問を解きたい人向け
講義:転がる正四面体は「頂点と周期性」がカギ
「平面上を滑ることなく転がる正四面体の動きを知りたい。」
注目すべきポイントは2つ。
「頂点」と「周期性」です。
- 頂点(面)のラベリング
→必須 - 周期性に注目
→必要に応じて
- 頂点(面)のラベリング
→必須 - 周期性に注目
→必要に応じて
その1.正四面体の頂点(面)の区別
まずは頂点(あるいは面)の「ラベリング」
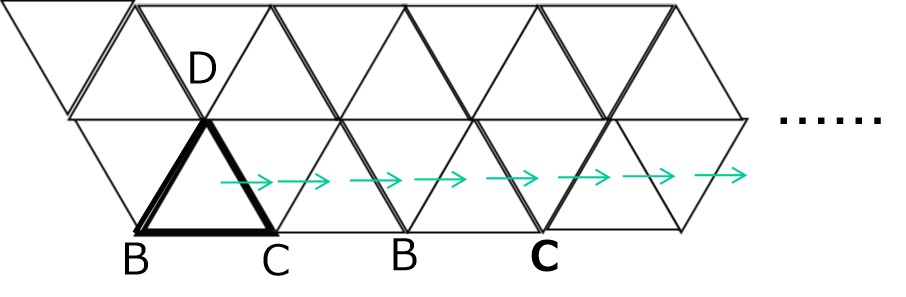
正四面体の頂点に、A,B,C,…などと名前を付ける、ということ。

そんなことして何になるの?
頂点を区別することで、正四面体の動きを「平面でとらえる」ことができるんです。
ここで例題を一つ。
【例題1】
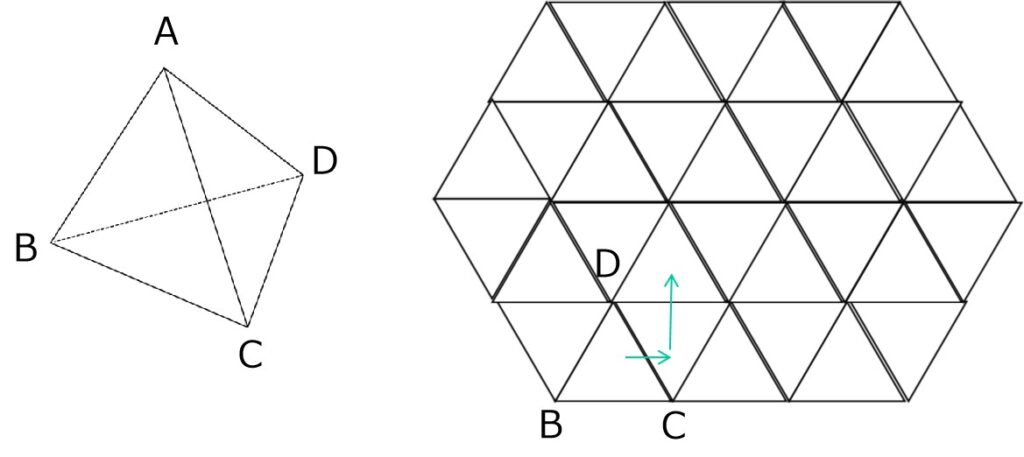
上にある頂点が「A」、底面の3頂点が「B, C, D」の正四面体があります。この正四面体を、三角形BCDを下にした状態で置き、マスの上を「右→上」の順に2回倒しました。このとき、地面についている面は三角形[ ]です。例題1:マス上を2回転がる正四面体 【解】
倒れた結果、
1回目…Aが地面に付く(Bが空中)
2回目…Bが地面に付く(Cが空中)
→結果、地面上の面は三角形ABD(答)2回の転がり→底面はABD
正四面体がマス目の上を転がる過程で、マスに頂点の名前(A,B,C…)を書き込んでいくと、どのタイミングにどの面が床にあるかを2Dで把握できますよね。
(分かりやすい!)

筆者的には頂点で区別するやり方がオススメ
その2.転がる正四面体の周期性に注目
次に、「周期性」
正四面体が転がるとき、頂点の現れ方に一定の規則があることを利用します。

難しそう。
その1みたいに1つずつ調べればいいんじゃないの?
周期性は、広大なフィールドでその真価を発揮します。
1万マス先、1億マス先(!)の頂点(面)も分かっちゃうスグレモノなんです。
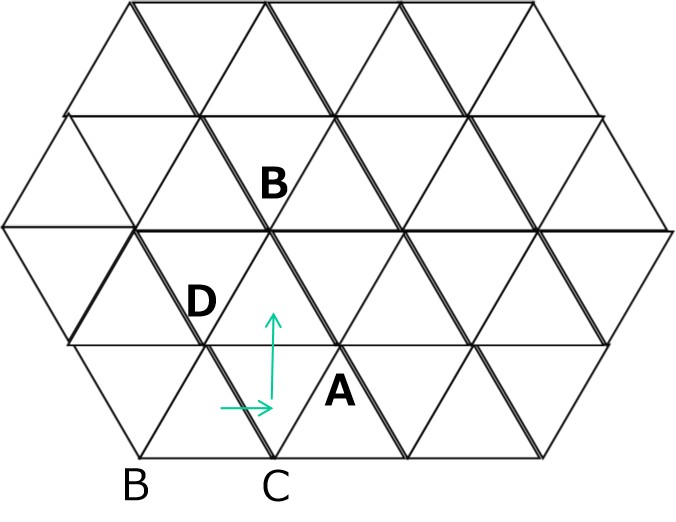
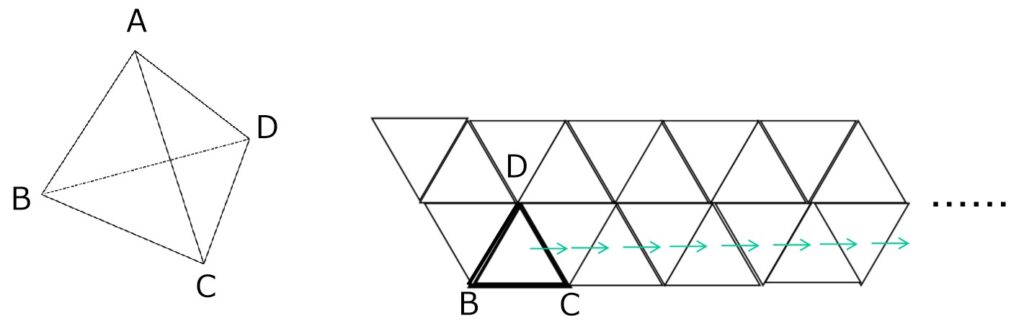
【例題2】
マス目のある無限に長い床の上に置いた正四面体AーBCDを、辺を軸として滑らないように右方向へ転がし続けるとき、はじめにCがあった点から数えて
(1)2個先の点は何か。
(2)1000個先の点は何か。例題2:一直線に転がる正四面体の頂点 【解】
(1)はじめのCから2個先、というのは転がる回数でいうと4回。
→C(答)
(この程度なら「その1」と同じように調べられる)頂点は「BCBC」のループ (2)(1)の図を見て、「(B→C→)B→C→B→C→…」というループに気づいてほしい。
1000個先なら、1000=500×2+0なので、C(答)
こんな風に、周期性が分かると「無限の彼方へ転がる正四面体」のことも分かっちゃうんです。
(スゴイ!)

それはすなわち神へと至る手段(?)
講義まとめ:正四面体のラベリングで周期性も
講義の内容をおさらい。
転がる正四面体の動きを追うために必要なのは、
頂点のラベリング
と
周期性

まずはラベリング、周期性は必要に応じて
問題:転がる正四面体の開始地点
底面に●印のある正四面体(図1)と、正四面体の面と同じ大きさの正三角形を敷きつめた模様(図2)の床がある。いま、図2のA~Fのいずれかに●印のある底面を合わせ、正四面体の辺を軸として床の上を滑ることなく転がし、太線のマスまで最短で移動することを考える。図2の太線のマスに、●印の面がちょうど重なるような開始地点を全て挙げたものとして正しいのは次のうちどれか。
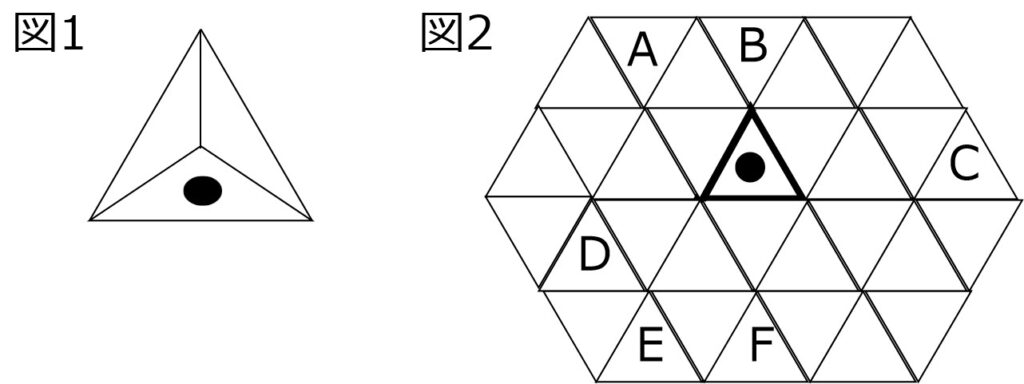
- AとC
- BとD
- BとF
- BとCとD
- BとCとE
5
設定は「A~F→太線」ですが、「太線→A~F」へ転がすと考えても全く同じ。
立体で考えることにとらわれるとハマります。
解説は筆者、「数的処理の穴場」管理者のモクセイがお送りします。
↑これでも元塾講で国家総合職の筆記合格者

おそすぎる自己紹介

購入方法↓
- 以下のボタンをクリックで購入画面へ
- 購入画面で支払い方法を選択&必要情報を入力、支払う→決済完了画面へ
- 決済完了画面に表示のURLから特設ページへアクセス
→ブックマーク推奨!
(URLが分からなくなったら記事名とともにsuutekimokusei@gmail.comまで) - 記事が読める!
※クリックすると決済画面(Stripe)へ移動します
Ω「モクセイにクレカ情報教えるのは嫌!AmazonPayかキャリア決済しか使いたくない!」
→note版もあります はい論破
ここまでお読みいただきありがとうございました。
「数的処理の穴場」では、算数・数学のオリジナル問題と【世界一ていねいな解説】をたくさん公開しています。
サイトに関するお知らせはXにて発信中。
新着記事の情報をいち早くお届けできますので、見逃さないようにぜひフォローをお願いします!
次回もお楽しみに!



コメント