サイコロの目の和

こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます！
本サイト、「数的処理の穴場」を運営しておりますモクセイと申します。

前回は、コンビニのおにぎりと購入者の対応関係を調べる問題でしたね。
どんな問題で、解法のどこがポイントだったか思い出せますか？
昨日解いた問題の内容を思い出すと記憶に定着しやすくなるので、ぜひ習慣化してみてください。
前置きはこれくらいにして、今日の問題に参りましょう！

本日の演習問題

非常にシンプルな問題ですが、サイコロの個数が決められていないところがクセものですね。
「色が全て異なる」とは、サイコロは全て区別できる、ということです。
よって(2, 3)と(3, 2)は別物としてカウントしなければなりません。
以下で詳しく解説します。
回りくどい説明が苦手な方は一番下の略解まで読み飛ばしてもOKです。

それではスタート！

詳しい解説

まずはサイコロの個数が決まっていないと調べようがありません。
そこで、サイコロが1個の場合、2個の場合、……と場合分けすることを考えましょう。
「出た目の和が6となる目の出方」が分かれば良いので、サイコロはたかだか6個までですね。

(i)サイコロが1個の場合
合計が6となるのは、6の目が出たときだけなので、1通り

(ii)サイコロが2個の場合
合計が6となる目の組み合わせは、(1, 5)、(2, 4)、(3, 3)の3パターンですね。
サイコロは区別されるので、(1, 5)、(2, 4)に関してはそれぞれ\(2!=2\)通りずつあります。
よって、この場合は全部で\(2+2+1=5\)通りです。

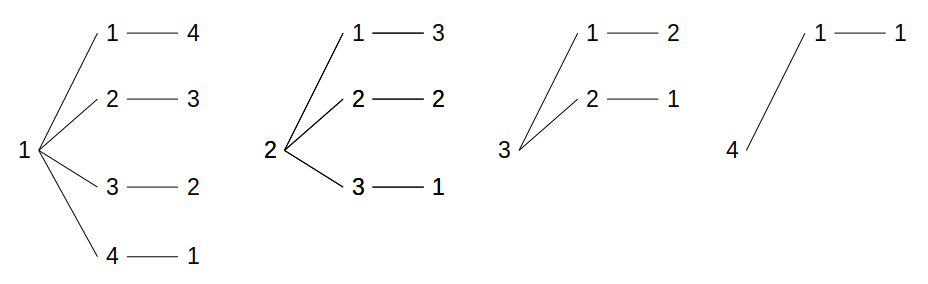
(iii)サイコロが3個の場合
合計が6となる目の組み合わせは、以下の樹形図によると10通りですね。

(iv)サイコロが4個の場合
合計が6となる組み合わせは、(1, 1, 1, 3)、(1, 1, 2, 2)の2パターンしかありません（理由は後述）。
同じものを含む順列として目の出方を数えると、
\[
\frac{4!}{3!1!}+\frac{4!}{2!2!}=4+6=10（通り）
\]

(v)サイコロが5個の場合
合計が6となる組み合わせは、(1, 1, 1, 1, 2)のみ（理由は後述）なので、
目の出方は\(\frac{5!}{4!1!}=5\)通りです。

(vi)サイコロが6個の場合
合計が6となるのは、全て1の目が出る1通りのみです。

以上、(i)〜(vi)の全てを足し合わせると、1+5+10+10+5+1=32通り
よって、２が正解となります。

補足：合計が6となる数字の組み合わせの考え方

ここでは、合計が6となる数字の組み合わせについて、以下の2つの場合を説明します。

• サイコロが4個の場合、なぜ(1, 1, 1, 3)、(1, 1, 2, 2)の2パターンだけなのか
• サイコロが5個の場合、なぜ(1, 1, 1, 1, 2)のみなのか

まず、サイコロが5個の場合の方が簡単なので、こちらから説明します。

いま、5個のサイコロに対応した5つの箱を用意します。
今回は組み合わせだけを扱うので、箱は区別しないで考えます。
これらの箱に、手元にある合計6個のボールを分けて入れることを考えます。

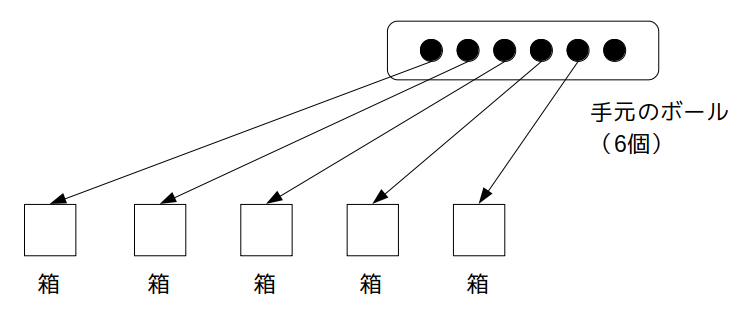
手元のボールが出目の合計値に、箱に入れたボールの個数が各サイコロの目にそれぞれ該当します。
この考え方でいくと、サイコロの目の最小値は1なので、5つの箱には少なくとも1つずつボールが入っていなくてはならないことになります。

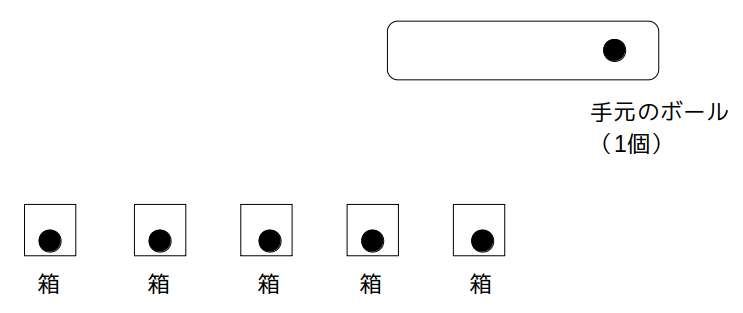
ボールを5つの箱に分配すると、手元は残り1個だけになりました。
この1個をどの箱に入れても、結局はボールが2個入った箱が1つだけある、という状況になります。
こうした考え方から、サイコロを5個振って合計が6となるような目の組み合わせは
(1, 1, 1, 1, 2)の1パターンしかありません。

これが、サイコロが5個の場合の出目の組み合わせの考え方です。

サイコロが4つの場合も、同様の考え方ができます。
まずは4つの箱A〜Dにボールを1個ずつ分配します。

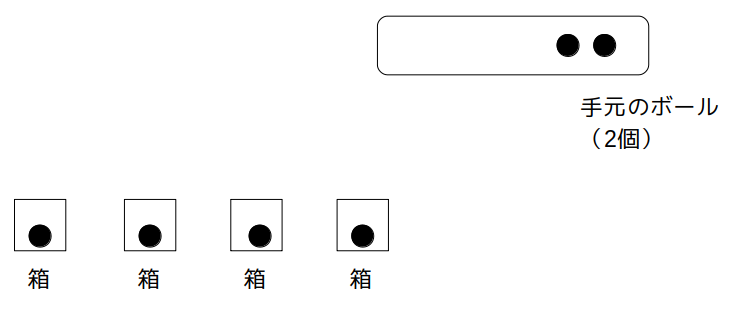
手元にはあと2つ、ボールが残っています。
これを4つの箱に分配することを考えるわけですが、分け方は結局以下のいずれかしかありません。

1. 2個をまとめて1つの箱に入れる
2. 2個を1個ずつ別の箱に入れる

アとイはそれぞれ(1, 1, 1, 3)、(1, 1, 2, 2)に該当するので、サイコロを4個振って合計が6となるような目の組み合わせはこの2パターンしかありません。

以上が、サイコロが4個または5個の場合に合計が6となる出目の組み合わせの考え方である。

おわりに

お疲れ様でした！
いかがだったでしょうか？

サイコロの出た目の和や積に関する問題は、巷でも割とよく見かけるテーマですよね。
使うサイコロを区別して、かつ個数が決められていない点が本問の大きな特徴でした。
しかし、使える個数は限られますし、場合分けで個数を決めてあげれば、あとは和が6となる目の出方を調べるという一種の典型問題に落とし込むことができます。
サイコロが4個の場合だけ少々厄介ですが、組み合わせが分からなければ樹形図を描いて数え上げてもOKです。
数的処理では、案外そういう原始的な方法が有効になる場面もあります。
ただ、数え上げる場合はヌケやモレがないように注意してください。
いずれにしても、国家総合職の教養試験なら、問題に応じて臨機応変に解法を選べるくらいの対応力はほしいところですね。
普段の勉強で、問題集に別解が載せられている場合は、併せて勉強することをおすすめします。
1つの問題で複数の解法を同時に学べるのは一石二鳥だと思います。
場合の数は単体で頻出分野であるだけでなく、確率とも関連が深いので対策は必須です。
「関連が深い」どころではなく、場合の数なしに確率を求めることは不可能でしょう。
今回の解説も参考にしつつ、場合の数の典型的な解き方を身に付けていってください！

本サイトでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！

次回もお楽しみに！

略解