整数の和

こんにちは。初めましての方は初めまして。ご覧いただきありがとうございます！
本ブログ、「数的処理の穴場」を運営しておりますモクセイと申します。

記念すべき第１回目、本日は以下の問題を解いていきましょう！

本日の演習問題

整数の和に関する問題ですね。一見すると単純そうですが、解法の糸口は掴めたでしょうか？
全く分からなかった貴方も、大丈夫。以下で詳しく解説します。
回りくどい説明は嫌だ、という方は一番下の略解まで読み飛ばしてもらっても大丈夫です。

それではスタート！

詳しい解説

この問題、まずは問題文中の「割り切れ『ない』」という表現に引っかかることが大切です。 「5でも7でも11でも割り切れる数の和」なら簡単なのにな……と考えられればあと一歩。
数学の定石で、余事象を数えて全体から差し引く、という考え方があります。

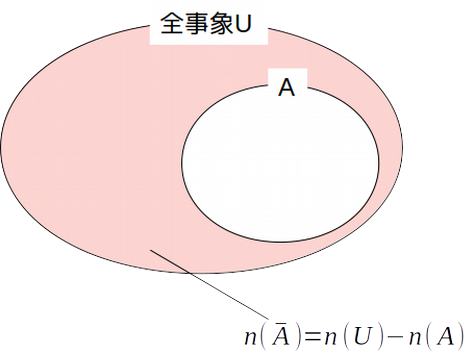
これを利用し、以下のようにして題意の値を求めます。

$$（5でも7でも11でも割り切れない数の和）＝（総和）-（5または7または11で割り切れる数の和）$$

この式より、次のステップでは「5または7または11で割り切れる数の和」を求めることになります。 そのためには、「P：5で割り切れる数（＝5の倍数）」「Q：7で割り切れる数（＝7の倍数）」 「R：11で割り切れる数（11の倍数）」という3つの集合について考える必要があります。 PまたはQまたはRである数の和を求めるには、以下の3集合の和の公式を利用します。

\begin{multline}
n(P \lor Q \lor R) = n(P)+n(Q)+n(R) \\
-n(P \land Q)-n(P \land R)-n(Q \land R)+n(P \land Q \land R)
\end{multline}

「\(P \land Q\)」、「\(P \land R\)」、「\(Q \land R\)」、「\(P \land Q \land R\)」は、
それぞれ「35の倍数」、「55の倍数」、「77の倍数」、「385の倍数」です。

これで必要な道具は全て揃ったので、あとは公式に数値を当てはめるだけです。

まず、5の倍数の和を求めましょう。1から560までの整数のうち、5の倍数は560÷5＝112個あります。「5の倍数の和」を「初項5、公差5、末項560、項数112の等差数列の和」と考えると、
以下のように求められます。

\[
\frac{(5+560)}{2} \times 112 = 31640
\]

以下、同様にして求めます。

7の倍数の和：
\[
\frac{(7+560)}{2} \times 80 = 22680
\]

11の倍数の和：
\[
\frac{(11+550)}{2} \times 50 = 14025
\]

35の倍数の和：
\[
\frac{(35+560)}{2} \times 16 = 4760
\]

55の倍数の和：
\[
\frac{(55+550)}{2} \times 10 = 3025
\]

77の倍数の和：
\[
\frac{(77+539)}{2} \times 7 = 2156
\]

385の倍数の和：\(385\)

よって、5または7または11で割り切れる数の和は

\[
31640 + 22680 + 14025 – 4760 – 3025 – 2156 + 385 = 58789
\]

さらに、5でも7でも11でも割り切れない数の和は

\[
157080 – 58789 = 98291
\]

題意は98291に一番近い数を選ぶことなので、正解は１となります。

おわりに

お疲れ様でした！
いかがだったでしょうか？

問題設定こそ単純なものの、きちんと向き合うと一筋縄では行かない問題でしたね。
解き方は分かっても、計算量が多くて正解にたどり着かなかったよ、という方もたくさんいると思います。
かくいう私も、解答を作るために一から解いたんですが、電卓には大いに助けられました（汗）
合格を目指すなら、時期にもよりますが、初めのうちは解答の方針が立てられれば十分だと思います。

本ブログでは、今後もこうした演習用の問題をアップしていく予定なので、ブックマークなどして気軽に訪れてもらえたらうれしいです。
また、運営のやる気UPと記事のクオリティアップにつながりますので、ご意見やご感想などありましたら、お気軽にコメントにてお知らせください！

次回もお楽しみに！

略解