こんにちは!
この記事では、中学受験の過去問みたいなオリジナル問題を【世界一ていねいな解説】とともに紹介しています。
今回のテーマ……展開図(立体図形)
立体図形の問題を、立体のまま思考していませんか?
3Dを頭の中に描くってしんどいですよね。
「俺/私は得意だから平気だよ」
と思ってても、無理のあるやり方はケアレスミスのもと。
早めの軌道修正をオススメします。

たまたま1回のミスが本番だったら……
ではどうするか。
3Dではない、「2D(平面)」で考えよ、ということ。
立体図形の平面で考える方法はいくつか※ありますが、今回は展開図を扱います。
その展開図で、必須ともいえるテクニックが「面移動」というやつ。

※ほかには…
断面図(切り口)や投影図なんかもある
今回は、展開図で面移動を使うことの4つのメリットをまとめました!
「面移動って何の役に立つの?」
「やり方は知ってるけど使いどころがよく分からない」
こんな疑問を解決していきます。
中学受験を突破したい全ての人へ向けた、転がるサイコロ問題の完全攻略ガイドです。
展開図を面移動で考える4つのメリット
立体図形の展開図で、面移動を使って問題を解く4つのメリットを紹介します。
- 向かい合う面が分かる
- 隣り合う面が分かる
- 立体の動き(転がり)にも対応
- 機械的に解ける

以下、立方体を例とし説明
1.展開図上で向かい合う面が分かる
展開図にはいくつかの形があります。
(いわゆる1-4-1型、1-3-2型、3-3型、2-2-2型)
→これって「1‐4‐1型」以外、一見するとどの面同士が向かい合うのか分かりづらいですよね。
1-3-2型、3-3型、2-2-2型の展開図で向かい合う面を知るのに役立つのが「面移動」
これら立方体の展開図は、面移動によって全て「1‐4‐1型(十字形)」に変形できます。
1‐4‐1型は、組み立てた形がイメージしやすくて素晴らしい。
向かい合う面もぱっと見で分かるので、展開図は面移動で「十字形」を作り出すのが定石なんです。
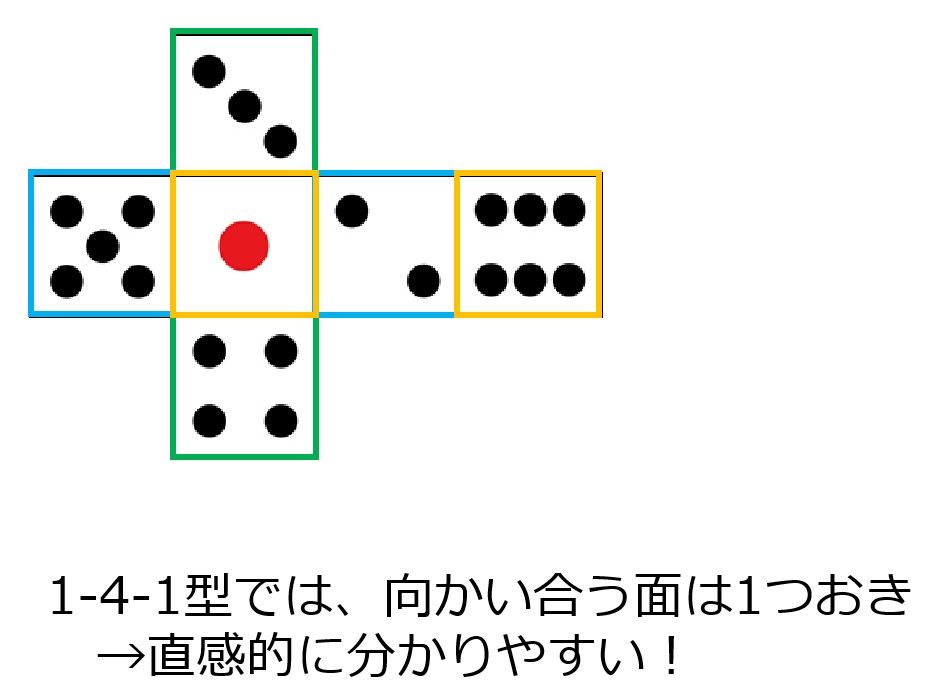

分かりにくいなら変形しちゃおうぜ
2.展開図上で隣り合う面が分かる
面移動があれば、ある面と隣り合う面が何なのかも展開図上で分かっちゃいます。
【例題】
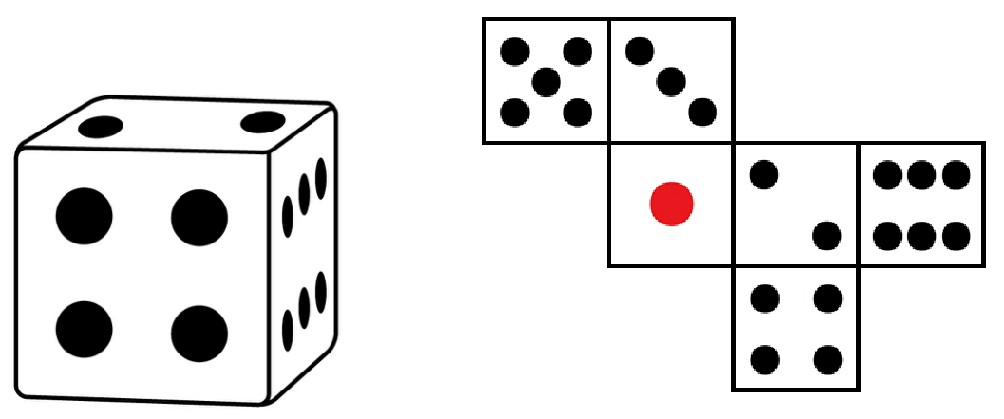
次の展開図を参考に、1の目と隣り合う目をすべて挙げよ。例題:サイコロの展開図
2と5は確定的に明らか。
では残り2つは?
問題の展開図からは(見た目では)分かりません。
そ・こ・で、面移動
1の目の周りに、面を集めてしまえばいいワケです。
3と4を、次のように持ってくることができます。
→2と3と4と5(答)
6以外、で即答できるのはナイショ
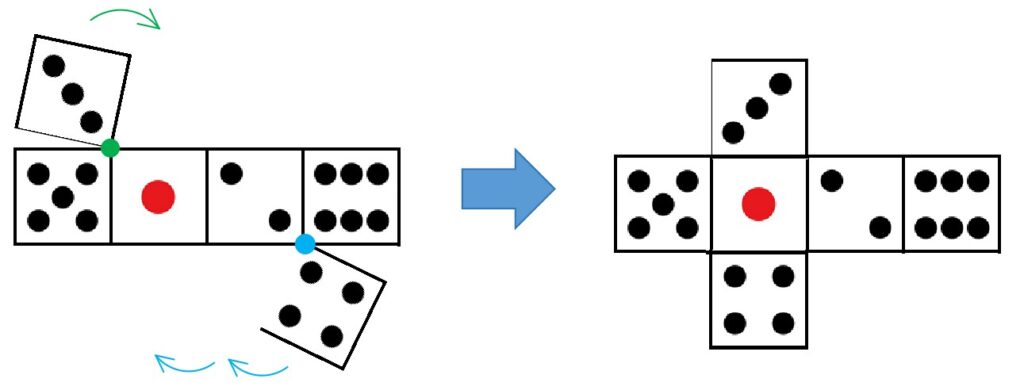
こんな風に、展開図上で隣り合う面を知りたいときにも面移動は有効です。

頭で想像したり暗記するより確実でしょ
3.立体の転がりにも対応できる
面移動があれば、転がりによる状況の変化も怖くない。
サイコロの問題では、「目の向き」もありがちテーマですよね。
転がったりし始めるとワケワカラン。
これも面移動で解決できます。
コロコロ状況が変わっても、面移動で展開図をアップデートしてやればいいだけだからです。
【例題】
図のようなサイコロを、次のように転がした時の上面の様子を描け。例題:サイコロと展開図 (1)手前へ1回転がしたとき
(2)(1)から、手前へさらに1回転がしたとき
図のサイコロを手前へ1回転がすと、2の目がスライドしてきて手前に来ます。
(代わりに、奥にあった面が上に見えている状態に変わる)
展開図でいうと、縦に並んだ面(2と4)が下へ平行移動して、4の代わりに2が視界の中心に来るイメージです。
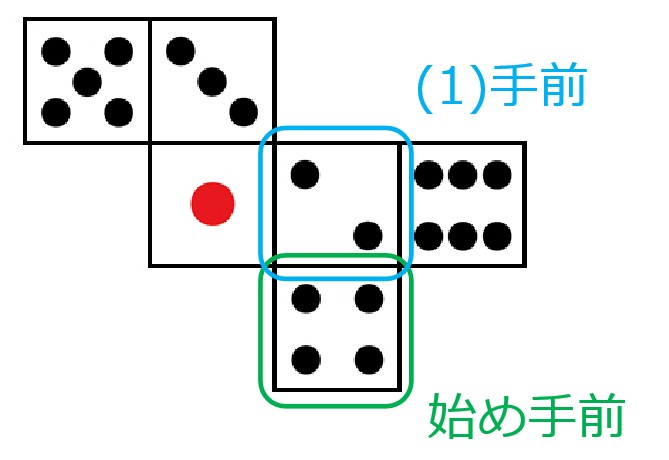

パチスロみたい
この例題だと、手前の面は「4→2→?→?→……」と切り替わります。
つまり、展開図で「2」の面の上にある面が分かればOK。
次図のように面移動すれば解決です。
→下図(答)
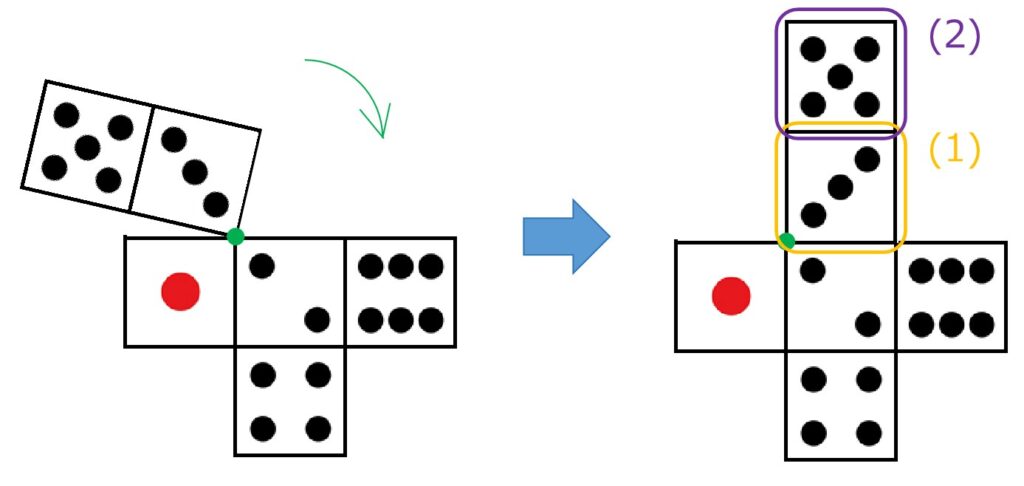
タテの並びを作ってやると、目の向きも含めて明らかとなるのがミソ。
今回は手前への回転だけなので1回の面移動で済みましたが、複雑な転がり方であっても同じ。
知りたいことに合わせて、展開図を都合よくカスタマイズしちゃいましょう。

ミルク多め、シロップ多め、氷少なめで
4.展開図の問題を機械的に解ける
これこそ、面移動の最大の強み。
頭のイメージで「なんとなく」で解いてしまいがちな立体図形を、平面上で論理的に思考するやり方が展開図の面移動。
実は面移動って、ある一つのシンプルな方針に従うだけなんです。
それは、
「十字形」に変形する
十字形は、立方体の展開図で最もポピュラー。
それだけに、「向かい合う面」「隣り合う面」「(ある面から見た)文字の向き」という、試験に出やすい情報を直感的に分かりやすい形で教えてくれます。

例題見て。全部十字形にしてる
展開図とは、すなわち「面移動で『十字形』を作る」ことと言ってもいいくらい。
試験本番は極度の緊張状態にあるからこそ、短絡化できるのは大変ありがたいですよね。
展開図は、面移動で「十字形」を目指すのが基本方針です。
立方体(サイコロ)の展開図は「十字形」が基本
→面移動で変形する
今回も、「展開図の面移動」をテーマとしたオリジナル問題を用意しました。
元塾講師で国公立大卒の筆者モクセイによる、【世界一ていねいな解説】です。
問題:サイコロの文字の向き
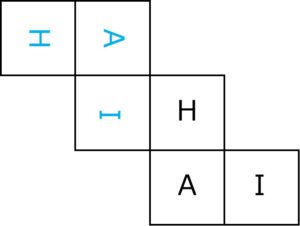
「A」「H」「I」が書かれた正方形のシールを、向かい合う面の文字およびその向きが一致するように立方体の各面に貼り付けてサイコロを作る。
次の問いに答えよ。
ただし「正位置」とは、最も手前の辺を下としたときの見え方を指すものとする。
例えば次図の場合、Aは赤線に対して「正位置」である。
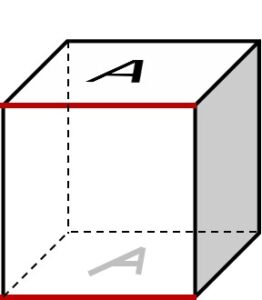
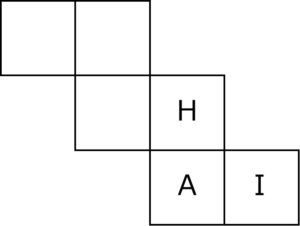
(1)図は、サイコロの展開図である。空白の面に、向きに注意して文字を書き入れ、展開図を完成させよ。
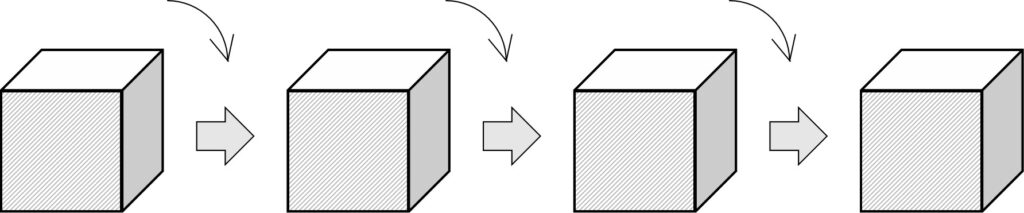
(2)サイコロを、上面に見える文字が正位置である状態から水平方向へ滑らずに1回転させたところ、上面に見える文字の向きはつねに正位置であった。このとき、手前の面に書かれた文字の見え方を図に正しく書き入れよ。
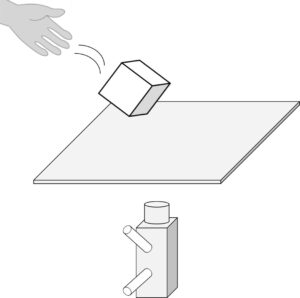
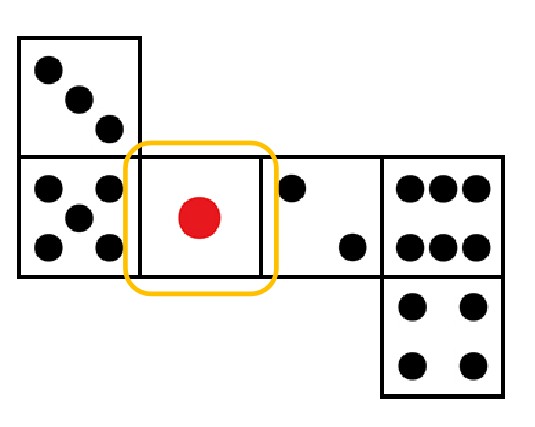
(3)図のように、透明な板の上でサイコロを3回振ったところ、板の下に固定したカメラの画像は次の通りであった。
- 1回目はIの正位置であった。
- 2回目と3回目の文字は同じであった。
これらを満たす手前の面の出方は何通りあるか。
(1)
(2)
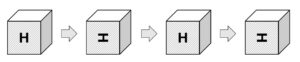
(3)17通り
解答時間:15分
キーワード:#サイコロの回転 #展開図 #向かい合う面 #文字の向き #場合分け
正解は分かりましたか?
解けた人は、答え合わせで自信が持てる。
そうでない人も大丈夫、解説を読んで正しい解き方を身につければいいだけ。
ぜひ、この後の解説を読んでいってください。
あなたの思考が「学び」に変わるチャンス、お見逃しなく。

ここで引き返すのはもったいない
解説:展開図の面移動で状況をつかむ
購入方法↓
- 以下のボタンをクリックで購入画面へ
- 購入画面で支払い方法を選択&必要情報を入力、支払う→決済完了画面へ
- 決済完了画面に表示のURLから特設ページへアクセス
→ブックマーク推奨!
(URLが分からなくなったら記事名とともにsuutekimokusei@gmail.comまで) - 記事が読める!
※クリックすると決済画面(Stripe)へ移動します
Ω「モクセイにクレカ情報教えるのは嫌!AmazonPayかキャリア決済しか使いたくない!」
→note版もあります はい論破
ここまでお読みいただきありがとうございました。
「数的処理の穴場」では、算数・数学のオリジナル問題と【世界一ていねいな解説】をたくさん公開しています。
サイトに関するお知らせはXにて発信中。
新着記事の情報をいち早くお届けできますので、見逃さないようにぜひフォローをお願いします!
次回もお楽しみに!




コメント